 |

|
Funciones que usan Pds::Matrix, Ejemplo: Pds::Sin(), Pds::Cos(), Pds::Exp(), Pds::Sqrt, etc. Más...
Namespaces | |
| namespace | Pds |
| Nombre de espacio para Pds (Procesamiento Digital de Senales) | |
Funciones trigonometricas | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| Pds::Matrix | Pds::Sin (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función seno. Más... | |
| Pds::Matrix | Pds::Cos (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función coseno. Más... | |
| Pds::Matrix | Pds::Tan (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función tangente. Más... | |
Funciones exponencial | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| Pds::Matrix | Pds::Exp (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función exponente. Más... | |
| Pds::Matrix | Pds::TwoExp (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función exponente de 2. Más... | |
| Pds::Matrix | Pds::Log (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función logaritmo natural. Más... | |
| Pds::Matrix | Pds::Ln (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función logaritmo natural. Más... | |
| Pds::Matrix | Pds::Log2 (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función logaritmo de base 2. Más... | |
| Pds::Matrix | Pds::Log10 (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función logaritmo de base 10. Más... | |
Funciones de potencia | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| Pds::Matrix | Pds::Sqrt (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función raiz cuadrada. Más... | |
| Pds::Matrix | Pds::Pow (const Pds::Matrix &A, double var) |
| Retorna el resultado de evaluar elemento a elemento la función pow. Más... | |
| Pds::Matrix | Pds::Pow (const Pds::Matrix &A, const Pds::Matrix &B) |
| Retorna el resultado de evaluar elemento a elemento la función pow. Más... | |
| Pds::Matrix | Pds::Atan2 (const Pds::Matrix &A, const Pds::Matrix &B) |
| Retorna el resultado de evaluar elemento a elemento la función atan2. Más... | |
Funciones pseudo Hb | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| double | Pds::XqHb (double p, double q) |
| Retorna el resultado de evaluar la función pseudo entropia $XqHb(p,q)$. Más... | |
| Pds::Matrix | Pds::XqHb (const Pds::Matrix &A, double q) |
| Retorna el resultado de evaluar la función pseudo entropia $XqHb(p,q)$. Más... | |
| double | Pds::DXqHb (double p, double q) |
| Retorna el resultado de evaluar la derivada de la función pseudo entropia $XqHb(p,q)$. Más... | |
| Pds::Matrix | Pds::DXqHb (const Pds::Matrix &A, double q) |
| Retorna el resultado de evaluar la derivada de la función pseudo entropia $XqHb(p,q)$. Más... | |
Funciones relativas a la Entropia binaria | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| double | Pds::PLog2P (double p) |
| Retorna el resultado de evaluar la función Pds::PLog2P(). Más... | |
| Pds::Matrix | Pds::PLog2P (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función Pds::PLog2P(). Más... | |
| double | Pds::CrossEntropy (double p, double q) |
| Retorna el resultado de evaluar la función Entropia binária. Más... | |
| Pds::Matrix | Pds::CrossEntropy (const Pds::Matrix &P, const Pds::Matrix &Q) |
| Retorna el resultado de evaluar la función Entropia binária. Más... | |
| double | Pds::KLDivergence (double p, double q) |
| Retorna el resultado de evaluar la Kullback–Leibler divergence. Más... | |
| Pds::Matrix | Pds::KLDivergence (const Pds::Matrix &P, const Pds::Matrix &Q) |
| Retorna el resultado de evaluar la Kullback–Leibler divergence. Más... | |
Funciones de Entropia binaria | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| double | Pds::Hb (double x) |
| Retorna el resultado de evaluar la función Entropia binária. Más... | |
| Pds::Matrix | Pds::Hb (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función Entropia binária. Más... | |
| double | Pds::HbInv (double h) |
| Retorna el valor | |
| Pds::Matrix | Pds::HbInv (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función inversa de la Entropia binária. Más... | |
| double | Pds::Logit2 (double x) |
| Retorna el resultado de evaluar la función logit. Más... | |
| Pds::Matrix | Pds::Logit2 (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función logit. Más... | |
| double | Pds::Hbn (double x) |
| Retorna el resultado de evaluar la función Entropia binária natural. Más... | |
| Pds::Matrix | Pds::Hbn (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función Entropia binária natural. Más... | |
Funciones Tsallis | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| double | Pds::qExp (double x, double q) |
| Retorna el resultado de evaluar la función q-exponent de Tsallis. Más... | |
| Pds::Matrix | Pds::qExp (const Pds::Matrix &A, double q) |
| Retorna el resultado de evaluar elemento a elemento la función q-exponent de Tsallis. Más... | |
| double | Pds::qLog (double x, double q) |
| Retorna el resultado de evaluar la función q-logaritmic de Tsallis. Más... | |
| Pds::Matrix | Pds::qLog (const Pds::Matrix &A, double q) |
| Retorna el resultado de evaluar elemento a elemento la función q-logaritmic de Tsallis. Más... | |
| double | Pds::qHbn (double x, double q) |
| Retorna el resultado de evaluar la función entropia de Tsallis. Más... | |
| Pds::Matrix | Pds::qHbn (const Pds::Matrix &A, double q) |
| Retorna el resultado de evaluar elemento a elemento la función entropia de Tsallis. Más... | |
| double | Pds::qDHbn (double x, double q) |
| Retorna el resultado de evaluar la derivada de la función entropia de Tsallis. Más... | |
| Pds::Matrix | Pds::qDHbn (const Pds::Matrix &A, double q) |
| Retorna el resultado de evaluar elemento a elemento la derivada función entropia de Tsallis. Más... | |
Funciones de Information Gain | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| double | Pds::InformationGain (const Pds::Matrix &B, const std::vector< Pds::Matrix > &A, double Umbral=0.5) |
| Retorna el Information Gain entre si mismo B y {A[0],A[1],...,A[N-1]}. Antes de comprarar las matrices se binarizan con el umbral Umbral. A[n]>Umbral, B>Umbral. Más... | |
| Pds::Vector | Pds::InformationGainScale (const Pds::Vector &Y, double Umbral=0.5) |
| Retorna un vector con todos los valores de Information Gain, dependiendo en donde se realice un corte en el vector | |
| Pds::Vector | Pds::InformationSumScale (const Pds::Vector &Y, double Umbral=0.5) |
| Retorna un vector con todos los valores de Information Sum, dependiendo en donde se realice un corte en el vector | |
Funciones Cumulative density functions | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| double | Pds::CDF::Phi (double x) |
| Calcula el valor de la función | |
| double | Pds::CDF::Phi (double x, double mu, double sigma) |
| Calcula el valor de la función | |
| Pds::Matrix | Pds::CDF::Phi (const Pds::Matrix &A) |
| Calcula el valor de la función | |
| double | Pds::CDF::Probit (double p) |
| Calcula el valor de la función | |
| Pds::Matrix | Pds::CDF::Probit (const Pds::Matrix &A) |
| Calcula el valor de la función | |
Funciones Estadisticas | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| double | Pds::Var (const Pds::Matrix &A, double *mean) |
| Calcula el valor de la varianza de la matriz A. Más... | |
| double | Pds::Var (const Pds::Matrix &A) |
| Calcula el valor de la varianza de la matriz A. Más... | |
| double | Pds::Mean (const Pds::Matrix &A) |
| Calcula el valor medio de los elementos de la matriz A. Más... | |
| double | Pds::Sum (const Pds::Matrix &A) |
| Calcula el valor de la suma de los elementos de la matriz A. Más... | |
| double | Pds::R2 (const Pds::Matrix &A, const Pds::Matrix &B) |
| Calcula el coeficiente de determinación o | |
| double | Pds::Accuracy (const Pds::Matrix &A, const Pds::Matrix &B, double Umbral=0.5) |
| Calcula el valor de la Accuracy entre los elementos de las matrices A y B. A>Umbral, B>Umbral. Más... | |
| double | Pds::AccuracyBatchBlock (const Pds::BatchBlock &A, const Pds::BatchBlock &B, double Umbral=0.5) |
| Calcula el valor de la Accuracy entre los elementos de las matrices A y B. A>Umbral, B>Umbral. Más... | |
| bool | Pds::CountRoundEqualIn (const Pds::Matrix &A, const Pds::Matrix &B, unsigned int &S, unsigned int &T) |
| Calcula el número de elementos enteros iguales entre las matrices A y B. Más... | |
| bool | Pds::CountRoundEqualInBatchBlock (const Pds::BatchBlock &A, const Pds::BatchBlock &B, unsigned int &S, unsigned int &T) |
| Calcula el número de elementos enteros iguales entre los objetos A y B. Más... | |
| bool | Pds::SquareErrorInBatchBlock (const Pds::BatchBlock &A, const Pds::BatchBlock &B, double &S) |
| Calcula el Square Error entre A y B. Más... | |
| double | Pds::NAccuracy (const Pds::Matrix &A, const Pds::Matrix &B) |
| Calcula el valor de la Accuracy entre los elementos de las matrices A y B. round(A), round(B). Más... | |
| double | Pds::MeanAbsoluteError (const Pds::Matrix &A, const Pds::Matrix &B) |
| Calcula el valor del error absoluto medio. Más... | |
Funciones de álgebra lineal | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| double | Pds::ArgMax (const Pds::Matrix &X) |
| Retorna el identicador (ID) de la posicion del máximo en la matriz. En caso de existir varios máximos la función retorna el primero en ser encontrado. Más... | |
| double | Pds::ArgMin (const Pds::Matrix &X) |
| Retorna el identicador (ID) de la posicion del mínimo en la matriz. En caso de existir varios mínimos la función retorna el primero en ser encontrado. Más... | |
| double | Pds::Det (const Pds::Matrix &A) |
| Calcula el valor de la detrminante de una matriz. Más... | |
| double | Pds::RMS (const Pds::Matrix &A) |
| Calcula el valor raiz quadrático medio de una matriz. Más... | |
| double | Pds::MeanAbsolute (const Pds::Matrix &A) |
| Calcula el valor absoluto medio de una matriz. Más... | |
| double | Pds::MeanSquare (const Pds::Matrix &A) |
| Calcula el valor quadrático medio de una matriz. Más... | |
| double | Pds::SumSquare (const Pds::Matrix &A) |
| Calcula el valor de la suma quadrática de una matriz. Más... | |
| double | Pds::Norm (const Pds::Matrix &A) |
| Calcula el valor dela norma (Frobenius) de una matriz. Más... | |
| double | Pds::NormDiff (const Pds::Matrix &A, const Pds::Matrix &B) |
| Calcula el valor dela norma (Frobenius) de una matriz. Más... | |
Funciones de activación | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| Pds::Matrix | Pds::SQNL (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la función SQNL. Más... | |
| double | Pds::SQNL (double x) |
| Retorna el resultado de evaluar la función SQNL. Más... | |
| Pds::Matrix | Pds::DSQNL (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la derivada de la función SQNL. Más... | |
| double | Pds::DSQNL (double x) |
| Retorna el resultado de evaluar la derivada de la función SQNL. Más... | |
| Pds::Matrix | Pds::Identity (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la función linear. Más... | |
| double | Pds::Identity (double x) |
| Retorna el resultado de evaluar la función linear. Más... | |
| Pds::Matrix | Pds::DIdentity (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la derivada de la función linear. Más... | |
| double | Pds::DIdentity (double x) |
| Retorna el resultado de evaluar la derivada de la función linear. Más... | |
| Pds::Matrix | Pds::SoftSign (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la función SoftSign. Más... | |
| double | Pds::SoftSign (double x) |
| Retorna el resultado de evaluar la función SoftSign. Más... | |
| Pds::Matrix | Pds::DSoftSign (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la derivada de la función SoftSign. Más... | |
| double | Pds::DSoftSign (double x) |
| Retorna el resultado de evaluar la derivada de la función SoftSign. Más... | |
| Pds::Matrix | Pds::ELU (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la función ELU. Más... | |
| double | Pds::ELU (double x) |
| Retorna el resultado de evaluar la función ELU. Más... | |
| Pds::Matrix | Pds::DELU (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la derivada de la función ELU. Más... | |
| double | Pds::DELU (double x) |
| Retorna el resultado de evaluar la derivada de la función ELU. Más... | |
| Pds::Matrix | Pds::SoftPlus (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la función SoftPlus. Más... | |
| double | Pds::SoftPlus (double x) |
| Retorna el resultado de evaluar la función SoftPlus. Más... | |
| Pds::Matrix | Pds::DSoftPlus (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la derivada de la función SoftPlus. Más... | |
| double | Pds::DSoftPlus (double x) |
| Retorna el resultado de evaluar la derivada de la función SoftPlus. Más... | |
| Pds::Matrix | Pds::ReLU (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la función ReLU. Más... | |
| double | Pds::ReLU (double x) |
| Retorna el resultado de evaluar la función ReLU. Más... | |
| Pds::Matrix | Pds::DReLU (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la derivada de la función ReLU. Más... | |
| double | Pds::DReLU (double x) |
| Retorna el resultado de evaluar la derivada de la función ReLU. Más... | |
| Pds::Matrix | Pds::LeakyReLU (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la función ReLU. Más... | |
| double | Pds::LeakyReLU (double x) |
| Retorna el resultado de evaluar la función Leaky ReLU. Más... | |
| Pds::Matrix | Pds::DLeakyReLU (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la derivada de la función ReLU. Más... | |
| double | Pds::DLeakyReLU (double x) |
| Retorna el resultado de evaluar la derivada de la función Leaky ReLU. Más... | |
| Pds::Matrix | Pds::Gaussian (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la función gaussiana. Más... | |
| double | Pds::Gaussian (double x) |
| Retorna el resultado de evaluar la función gaussiana. Más... | |
| Pds::Matrix | Pds::DGaussian (const Pds::Matrix &X) |
| Retorna el resultado de evaluar la función gaussiana. Más... | |
| double | Pds::DGaussian (double x) |
| Retorna el resultado de evaluar la función gaussiana. Más... | |
| Pds::Matrix | Pds::Tanh (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la función tangente hiperbólico. Más... | |
| double | Pds::Tanh (double x) |
| Retorna el resultado de evaluar la función tangente hiperbólico. Más... | |
| Pds::Matrix | Pds::DTanh (const Pds::Matrix &X) |
| Retorna el resultado de evaluar la derivada de la función tangente hiperbólico. Más... | |
| double | Pds::DTanh (double x) |
| Retorna el resultado de evaluar la derivada de la función tangente hiperbólico. Más... | |
| Pds::Matrix | Pds::Sigmoid (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la función sigmoid. Más... | |
| double | Pds::Sigmoid (double x) |
| Retorna el resultado de evaluar elemento a elemento la función sigmoid. Más... | |
| Pds::Matrix | Pds::DSigmoid (const Pds::Matrix &X) |
| Retorna el resultado de evaluar elemento a elemento la derivada de la función sigmoid. Más... | |
| double | Pds::DSigmoid (double x) |
| Retorna el resultado de evaluar elemento a elemento la derivada de la función sigmoid. Más... | |
Funciones de activación multiple | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| Pds::Matrix | Pds::SoftMax (const Pds::Matrix &X) |
| Retorna el resultado de evaluar la función SoftMax. Más... | |
| Pds::Matrix | Pds::HardMax (const Pds::Matrix &X) |
| Retorna el resultado de evaluar la función HardMax (ArgMax in Machine learning). Más... | |
Funcione de analisis combinatorio | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| unsigned int | Pds::Factorial (unsigned int n) |
| Evalúa factorial de n, igual a n!. Más... | |
| unsigned int | Pds::NchooseK (unsigned int n, unsigned int k) |
| Retorna el combinatorio (n,k) Más... | |
| unsigned int | Pds::NmultichooseK (unsigned int n, unsigned int k) |
| Retorna el combinatorio (n,k) Más... | |
Funciones de aredondamento a enteros | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| double | Pds::UnitStep (double x) |
| Retorna el resultado de evaluar la función UnitStep(). Más... | |
| Pds::Matrix | Pds::UnitStep (const Pds::Matrix &A) |
| Retorna el resultado de evaluar la función UnitStep(). Más... | |
| double | Pds::UnitRamp (double x) |
| Retorna el resultado de evaluar la función UnitRamp(). Más... | |
| Pds::Matrix | Pds::UnitRamp (const Pds::Matrix &A) |
| Retorna el resultado de evaluar la función UnitRamp(). Más... | |
| double | Pds::SignNZ (double x) |
| Retorna el resultado de evaluar la función Sign Non Zero. Más... | |
| double | Pds::Sign (double x) |
| Retorna el resultado de evaluar la función Sign. Más... | |
| Pds::Matrix | Pds::Sign (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función Sign. Más... | |
| Pds::Matrix | Pds::Round (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función round. Más... | |
Funciones de telecomunicaciones | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| double | Pds::MuLaw (double x, double Mu) |
| Retorna el resultado de evaluar la | |
| Pds::Matrix | Pds::MuLaw (const Pds::Matrix &A, double Mu) |
| Retorna el resultado de evaluar la | |
| double | Pds::MuLawInv (double y, double Mu) |
| Retorna el resultado de evaluar la | |
| Pds::Matrix | Pds::MuLawInv (const Pds::Matrix &A, double Mu) |
| Retorna el resultado de evaluar la | |
Funciones relativas a la convolução | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| Pds::Matrix | Pds::Conv2DCh (const std::vector< Pds::Matrix > &A, const std::vector< Pds::Matrix > &Kernel, const std::vector< unsigned int > &Strides={1, 1}, Pds::Ra::Padding Padding=Pds::Ra::Valid) |
| Calcula la convolución de todos los canales entre A y Kernel. Más... | |
| Pds::Vector | Pds::Conv1DCh (const std::vector< Pds::Vector > &A, const std::vector< Pds::Vector > &Kernel, unsigned int Strides=1, Pds::Ra::Padding Padding=Pds::Ra::Valid) |
| Calcula la convolución de todos los canales entre A y Kernel. Más... | |
| Pds::Matrix | Pds::Conv1DCh (const std::vector< Pds::Matrix > &A, const std::vector< Pds::Vector > &Kernel, unsigned int Strides=1, Pds::Ra::Padding Padding=Pds::Ra::Valid) |
| Calcula la convolución de todos los canales entre A y Kernel. Más... | |
Funciones varias | |
Descripcion de algunas funciónes matematicas que usan Pds::Matrix. | |
| Pds::Matrix | Pds::Abs (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función valor absoluto. Más... | |
| double | Pds::Logit (double x) |
| Retorna el resultado de evaluar la función logit. Más... | |
| Pds::Matrix | Pds::Logit (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función logit. Más... | |
| Pds::Matrix | Pds::Erf (const Pds::Matrix &A) |
| Calcula el valor de la función | |
| double | Pds::Sinc (double x) |
| Retorna el resultado de evaluar la función sinc. Más... | |
| Pds::Matrix | Pds::Sinc (const Pds::Matrix &A) |
| Retorna el resultado de evaluar elemento a elemento la función sinc. Más... | |
Funciones que usan Pds::Matrix, Ejemplo: Pds::Sin(), Pds::Cos(), Pds::Exp(), Pds::Sqrt, etc.
Estas funciónes trabajan con una matriz de la forma.
![\[
\mathbf{A}=\left(\begin{matrix}
a_{00} & a_{01} & \cdots & a_{0(Ncol-1)}\\
a_{10} & a_{11} & \cdots & a_{1(Ncol-1)}\\
\vdots & \vdots & \vdots & \vdots \\
a_{(Nlin-2)0} & a_{(Nlin-2)1} & \cdots & a_{(Nlin-2)(Ncol-1)}\\
a_{(Nlin-1)0} & a_{(Nlin-1)1} & \cdots & a_{(Nlin-1)(Ncol-1)}\\
\end{matrix}\right)
\]](form_107.png)
![]()
nlin es el número de lineas y ncol es el número de columnas.
Informacion adicional puede ser encontrada en [5]
| Pds::Matrix Pds::Sin | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función seno.
![]()
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::Cos | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función coseno.
![]()
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::Tan | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función tangente.
![]()
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::Exp | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función exponente.
![]()
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::TwoExp | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función exponente de 2.
![]()
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::Log | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función logaritmo natural.
![]()
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::Ln | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función logaritmo natural.
![]()
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::Log2 | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función logaritmo de base 2.
![]()
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::Log10 | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función logaritmo de base 10.
![]()
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::Sqrt | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función raiz cuadrada.
![]()
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::Pow | ( | const Pds::Matrix & | A, |
| double | var | ||
| ) |
Retorna el resultado de evaluar elemento a elemento la función pow.
![]()
| [in] | A | La matriz a evaluar |
| [in] | var | La variable a evaluar |
| Pds::Matrix Pds::Pow | ( | const Pds::Matrix & | A, |
| const Pds::Matrix & | B | ||
| ) |
Retorna el resultado de evaluar elemento a elemento la función pow.
![]()
| [in] | A | La matriz a evaluar |
| [in] | B | La matriz a evaluar |
| Pds::Matrix Pds::Atan2 | ( | const Pds::Matrix & | A, |
| const Pds::Matrix & | B | ||
| ) |
Retorna el resultado de evaluar elemento a elemento la función atan2.
![]()
| [in] | A | La matriz a evaluar |
| [in] | B | La matriz a evaluar |
| double Pds::XqHb | ( | double | p, |
| double | q | ||
| ) |
Retorna el resultado de evaluar la función pseudo entropia $XqHb(p,q)$.
![\[
XqHb(p,q)=\begin{cases}
0 & \text{ if } ~ p\leq 0 \\
\left(\frac{p}{0.5}\right)^q & \text{ if } ~ 0<p<0.5\\
1 & \text{ if } ~ p=0.5 \\
\left(\frac{1-p}{0.5}\right)^q & \text{ if } ~ 0.5<p<1\\
0 & \text{ if } ~ 1\leq p \\
\end{cases}
\]](form_356.png)
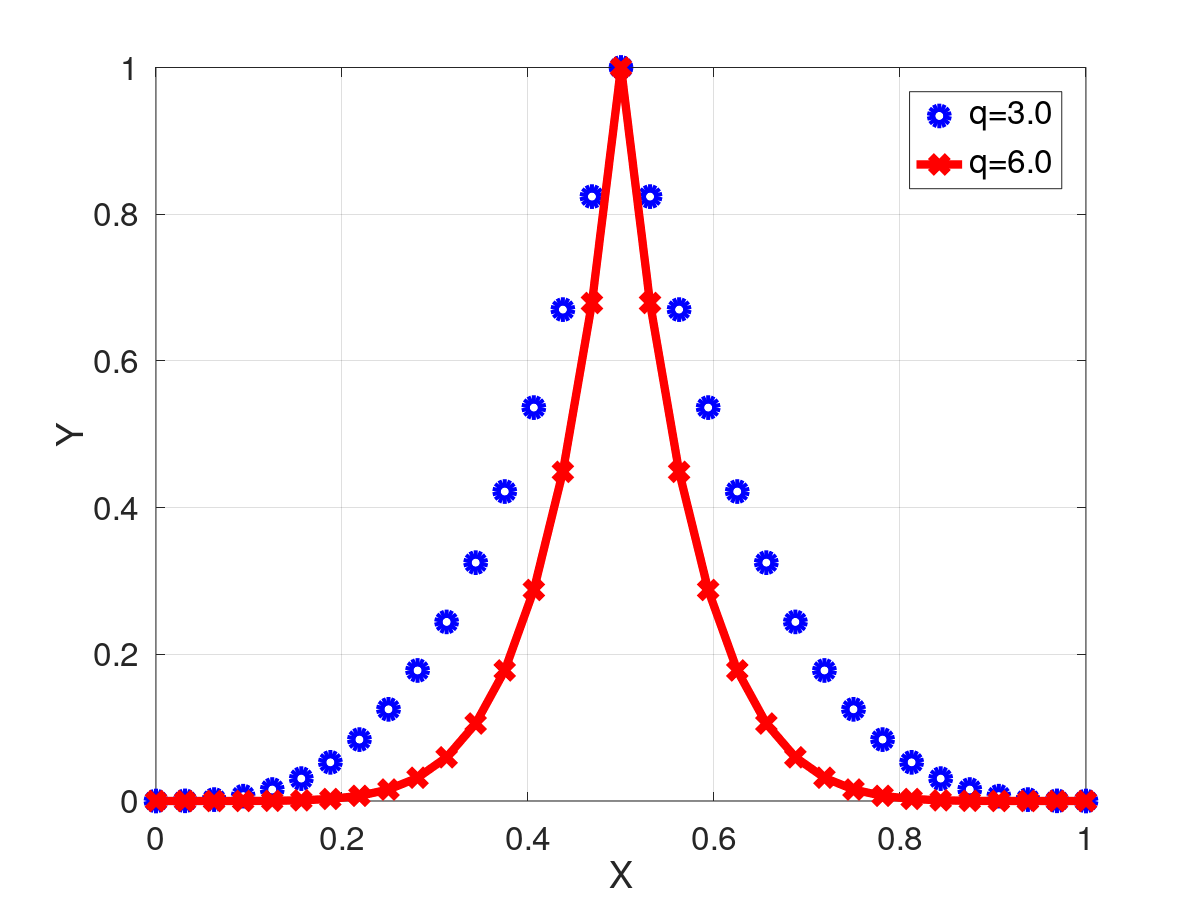
| [in] | p | La variable a evaluar |
| [in] | q | parámetro potencia. |
| Pds::Matrix Pds::XqHb | ( | const Pds::Matrix & | A, |
| double | q | ||
| ) |
Retorna el resultado de evaluar la función pseudo entropia $XqHb(p,q)$.
![\[
XqHb(p,q)=\begin{cases}
0 & \text{ if } ~ p\leq 0 \\
\left(\frac{p}{0.5}\right)^q & \text{ if } ~ 0<p<0.5\\
1 & \text{ if } ~ p=0.5 \\
\left(\frac{1-p}{0.5}\right)^q & \text{ if } ~ 0.5<p<1\\
0 & \text{ if } ~ 1\leq p \\
\end{cases}
\]](form_356.png)
![]()

| [in] | A | La matriz a evaluar |
| [in] | q | parámetro potencia. |
| double Pds::DXqHb | ( | double | p, |
| double | q | ||
| ) |
Retorna el resultado de evaluar la derivada de la función pseudo entropia $XqHb(p,q)$.
![\[
DXqHb(p,q)=\begin{cases}
0 & \text{ if } ~ p\leq 0 \\
+2q\left(\frac{p}{0.5}\right)^{q-1} & \text{ if } ~ 0<p<0.5\\
\pm 2q & \text{ if } ~ p=0.5 \text{ with~random~signal }\\
-2q\left(\frac{1-p}{0.5}\right)^{q-1} & \text{ if } ~ 0.5<p<1\\
0 & \text{ if } ~ 1\leq p \\
\end{cases}
\]](form_358.png)
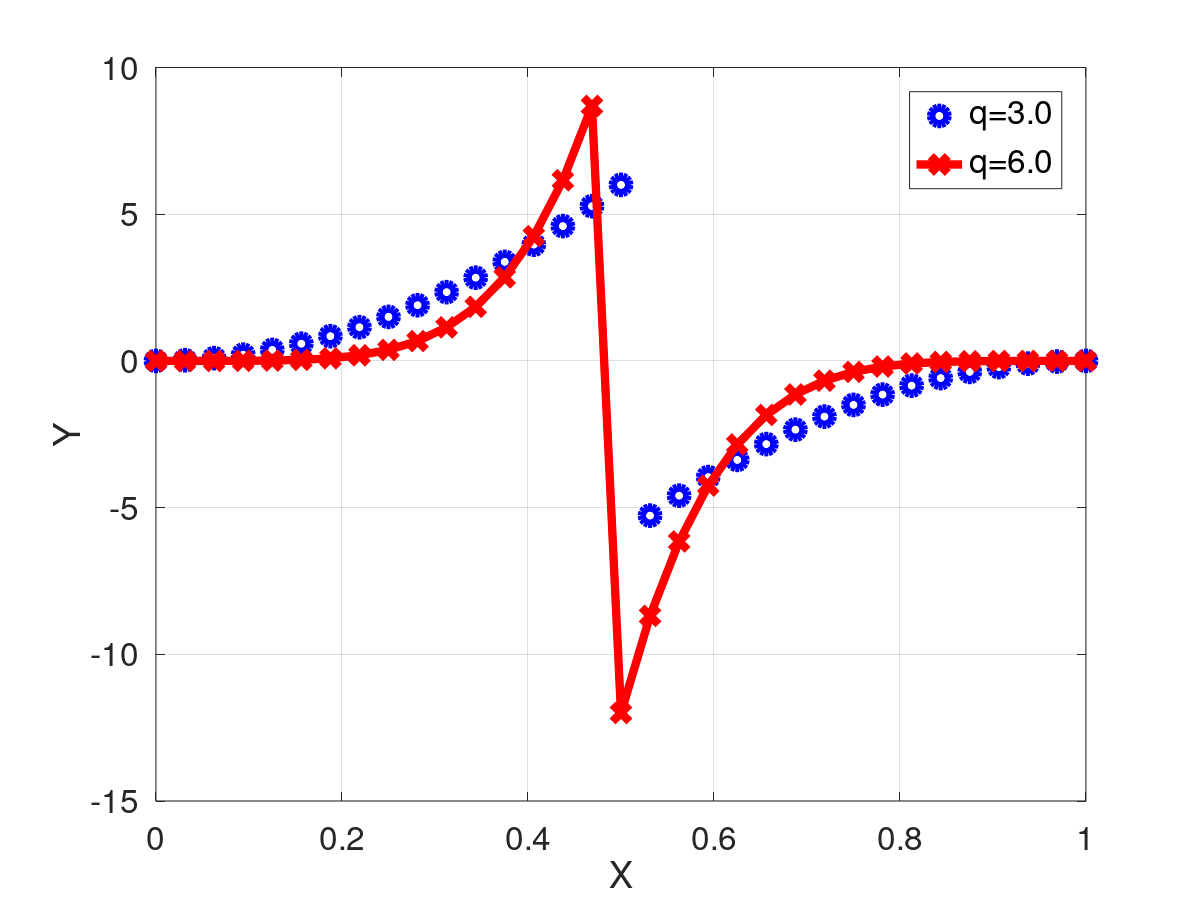
| [in] | p | La variable a evaluar |
| [in] | q | parámetro potencia. |
| Pds::Matrix Pds::DXqHb | ( | const Pds::Matrix & | A, |
| double | q | ||
| ) |
Retorna el resultado de evaluar la derivada de la función pseudo entropia $XqHb(p,q)$.
![\[
DXqHb(p,q)=\begin{cases}
0 & \text{ if } ~ p\leq 0 \\
+2q\left(\frac{p}{0.5}\right)^{q-1} & \text{ if } ~ 0<p<0.5\\
\pm 2q & \text{ if } ~ p=0.5 \text{ with~random~signal }\\
-2q\left(\frac{1-p}{0.5}\right)^{q-1} & \text{ if } ~ 0.5<p<1\\
0 & \text{ if } ~ 1\leq p \\
\end{cases}
\]](form_358.png)
![]()

| [in] | A | La matriz a evaluar |
| [in] | q | parámetro potencia. |
| double Pds::PLog2P | ( | double | p | ) |
Retorna el resultado de evaluar la función Pds::PLog2P().
![\[ PLog2P(p)=\begin{cases}
0 & \text{ if } p=0 \\
p~log_2(p) & \text{ else }
\end{cases}
\]](form_360.png)
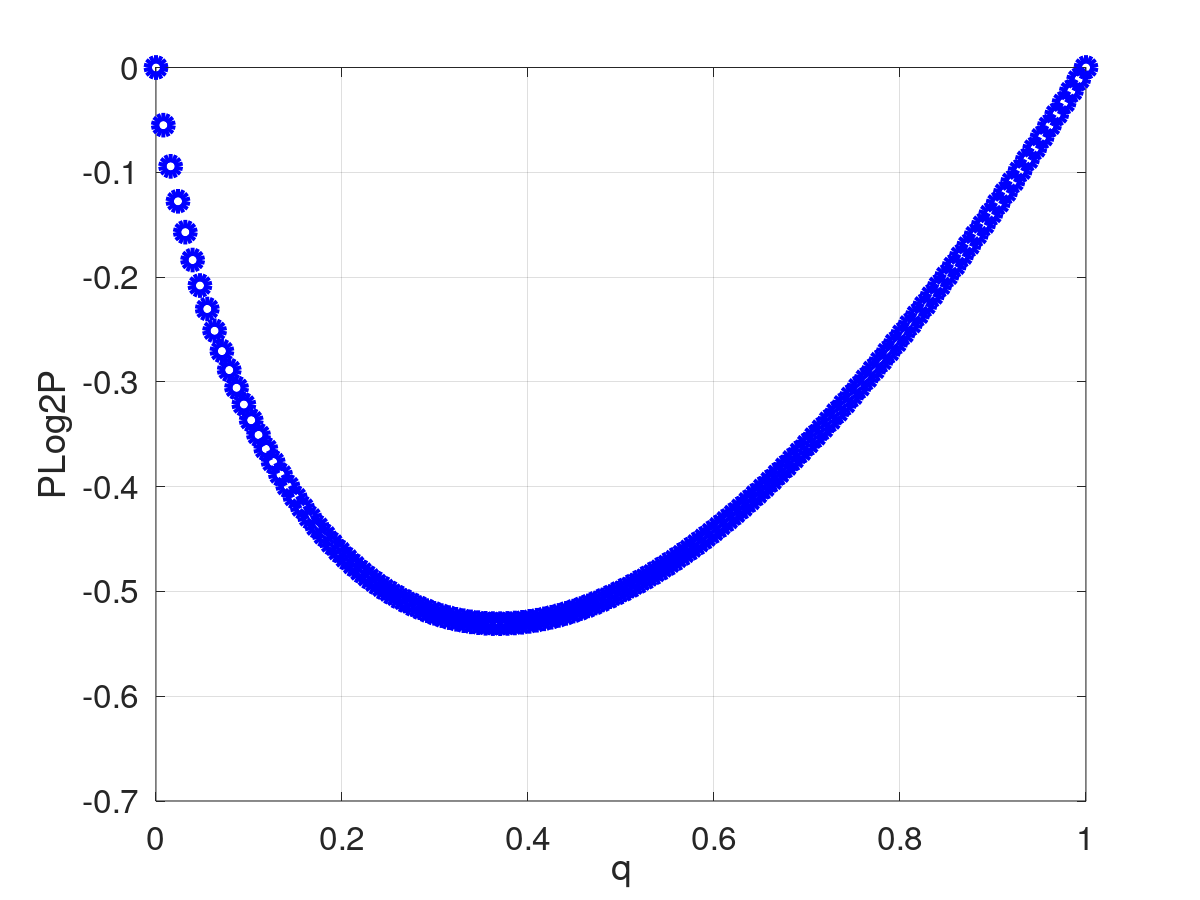
| [in] | p | La variable a evaluar |
| Pds::Matrix Pds::PLog2P | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función Pds::PLog2P().
![\[ PLog2P(p)=\begin{cases}
0 & \text{ if } p=0 \\
p~log_2(p) & \text{ else }
\end{cases}
\]](form_360.png)

![]()
| [in] | A | La matriz a evaluar |
| double Pds::CrossEntropy | ( | double | p, |
| double | q | ||
| ) |
Retorna el resultado de evaluar la función Entropia binária.
![]()
![]()
| Pds::CrossEntropy(0.0,0.0): | 0 |
| Pds::CrossEntropy(0.0,1.0): | inf |
| Pds::CrossEntropy(1.0,0.0): | inf |
| Pds::CrossEntropy(1.0,1.0): | 0 |
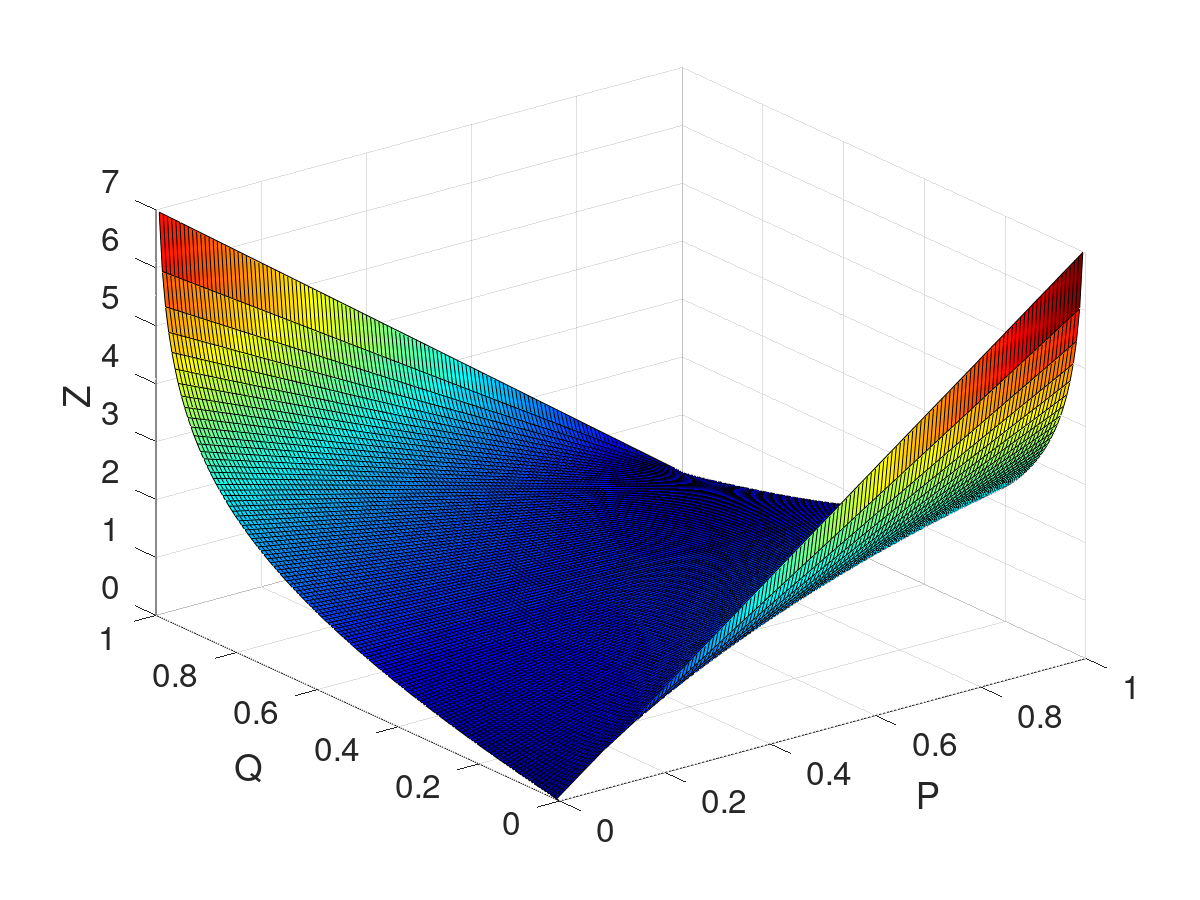
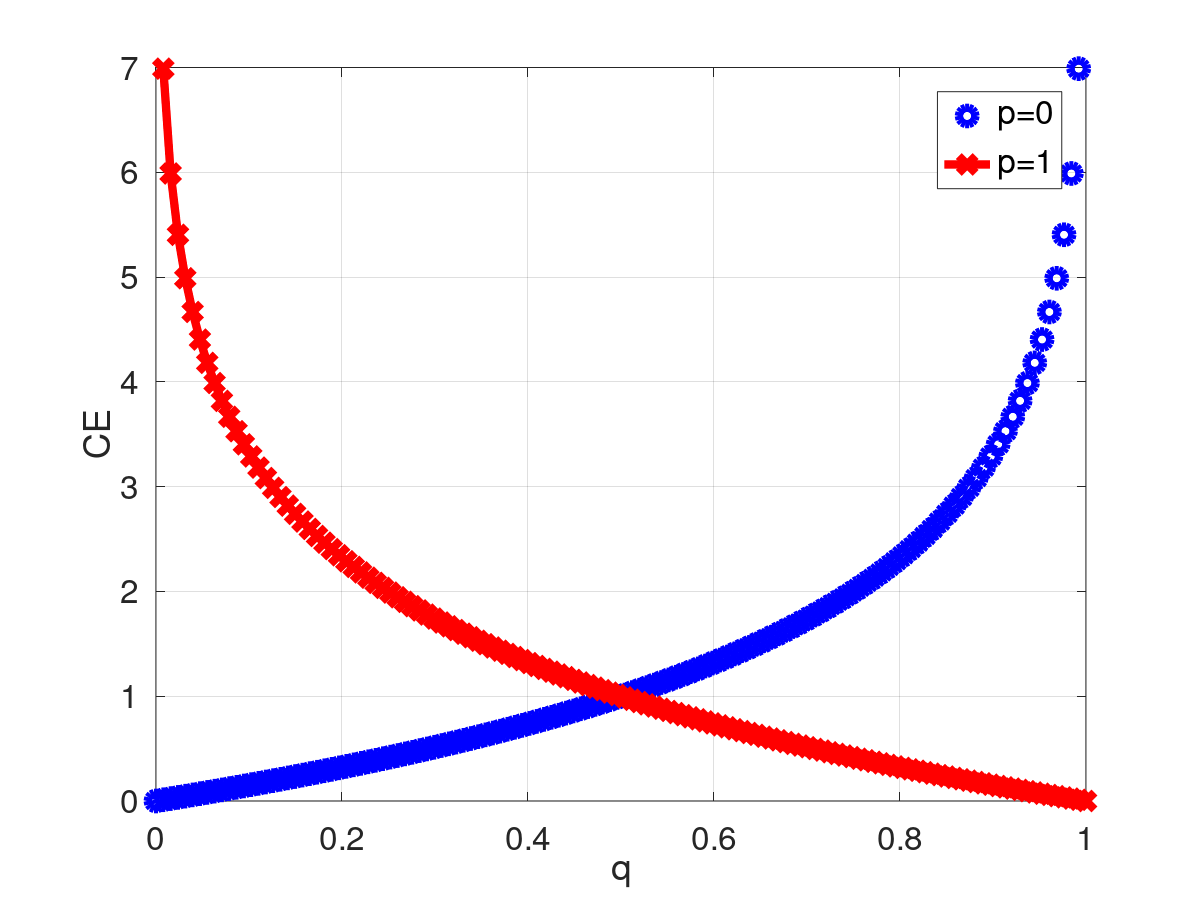
| [in] | p | La primeira probabilidade. |
| [in] | q | La segunda probabilidade. |
| Pds::Matrix Pds::CrossEntropy | ( | const Pds::Matrix & | P, |
| const Pds::Matrix & | Q | ||
| ) |
Retorna el resultado de evaluar la función Entropia binária.
![]()
![]()
| Pds::CrossEntropy(0.0,0.0): | 0 |
| Pds::CrossEntropy(0.0,1.0): | inf |
| Pds::CrossEntropy(1.0,0.0): | inf |
| Pds::CrossEntropy(1.0,1.0): | 0 |


| [in] | P | La primeira probabilidade. |
| [in] | Q | La segunda probabilidade. |
| double Pds::KLDivergence | ( | double | p, |
| double | q | ||
| ) |
Retorna el resultado de evaluar la Kullback–Leibler divergence.
![\[ Pds::KLDivergence(p,q)=-p~log_2\left(\frac{q}{p}\right)-(1-p) log_2\left(\frac{1-q}{1-p}\right) \]](form_364.png)
![]()
| Pds::KLDivergence(0.0,0.0): | 0 |
| Pds::KLDivergence(0.0,1.0): | inf |
| Pds::KLDivergence(1.0,0.0): | inf |
| Pds::KLDivergence(1.0,1.0): | 0 |
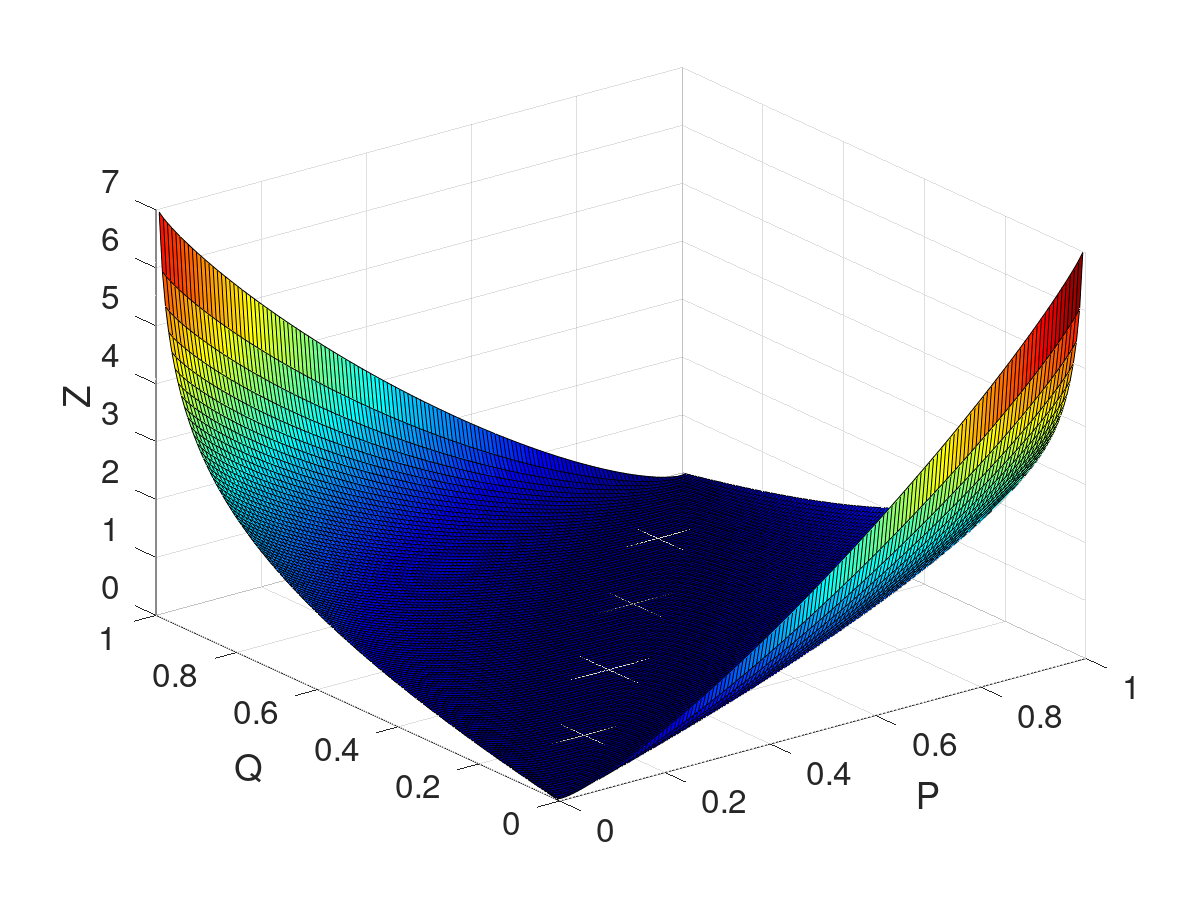
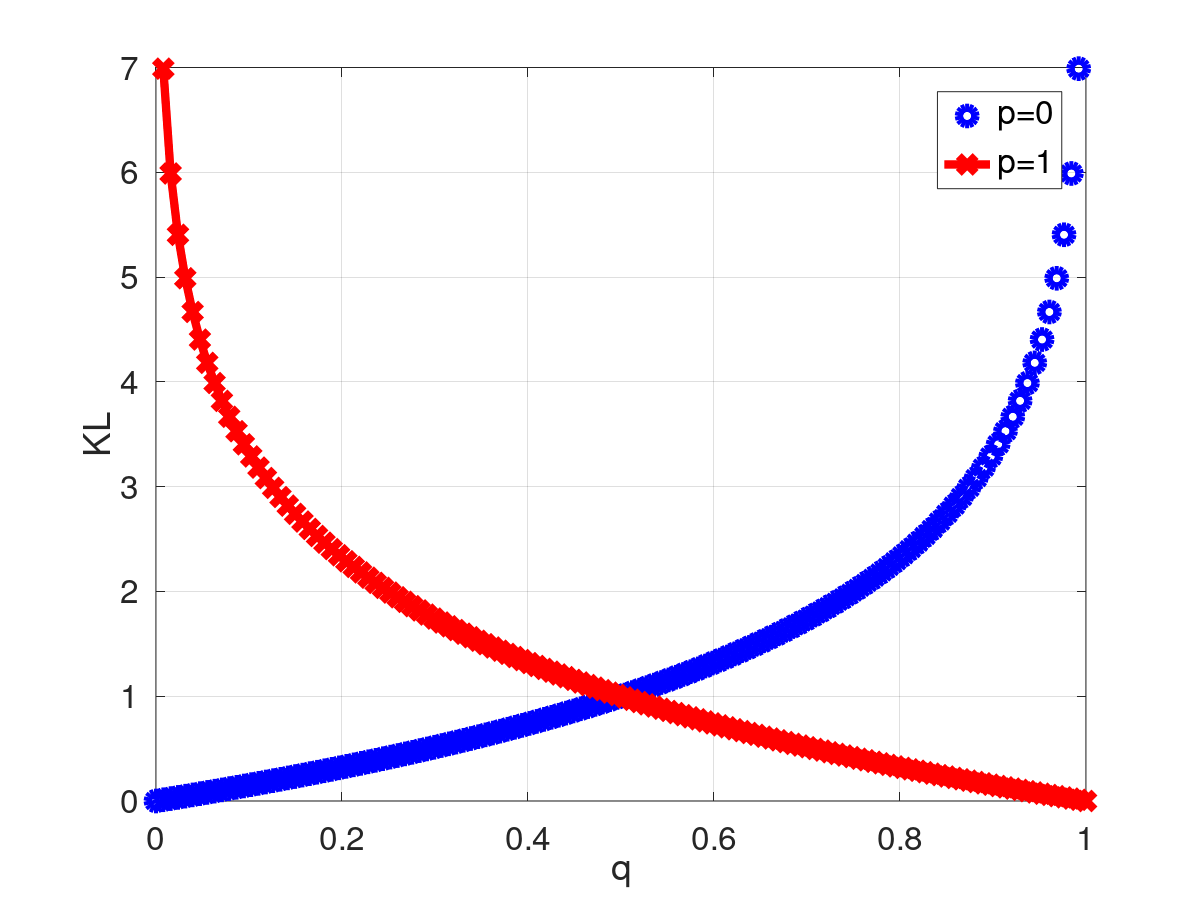
| [in] | p | La primeira probabilidade. |
| [in] | q | La segunda probabilidade. |
| Pds::Matrix Pds::KLDivergence | ( | const Pds::Matrix & | P, |
| const Pds::Matrix & | Q | ||
| ) |
Retorna el resultado de evaluar la Kullback–Leibler divergence.
![\[ Pds::KLDivergence(p,q)=-p~log_2\left(\frac{q}{p}\right)-(1-p) log_2\left(\frac{1-q}{1-p}\right) \]](form_364.png)
![]()
| Pds::KLDivergence(0.0,0.0): | 0 |
| Pds::KLDivergence(0.0,1.0): | inf |
| Pds::KLDivergence(1.0,0.0): | inf |
| Pds::KLDivergence(1.0,1.0): | 0 |


| [in] | P | La primeira probabilidade. |
| [in] | Q | La segunda probabilidade. |
| double Pds::Hb | ( | double | x | ) |
Retorna el resultado de evaluar la función Entropia binária.
![]()
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::Hb | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función Entropia binária.
![]()
![]()
| [in] | A | La matriz a evaluar |
| double Pds::HbInv | ( | double | h | ) |
Retorna el valor ![]() de la función de entropía binaria para un valor de
de la función de entropía binaria para un valor de ![]() .
.
![]()
| [in] | h | Valor de entrada. |
| Pds::Matrix Pds::HbInv | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función inversa de la Entropia binária.
![]()
| [in] | A | La matriz a evaluar |
| double Pds::Logit2 | ( | double | x | ) |
Retorna el resultado de evaluar la función logit.
![\[ log_2\left(\frac{x}{1-x}\right) \equiv -\frac{d~H_b(x)}{dx}\]](form_372.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::Logit2 | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función logit.
![\[ log_2\left(\frac{A}{1-A}\right) \equiv -\frac{d~H_b(x)}{dx}\]](form_373.png)
| [in] | A | La matriz a evaluar |
| double Pds::Hbn | ( | double | x | ) |
Retorna el resultado de evaluar la función Entropia binária natural.
![]()
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::Hbn | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función Entropia binária natural.
![]()
![]()
| [in] | A | La matriz a evaluar |
| double Pds::qExp | ( | double | x, |
| double | q | ||
| ) |
Retorna el resultado de evaluar la función q-exponent de Tsallis.
![\[
qExp(x) = \begin{cases}
e^{x} & \text{if }q=1, \\[6pt]
[1+(1-q)x]^{1/(1-q)} & \text{if }q \ne 1 \text{ and } 1+(1-q)x >0, \\[6pt]
0^{1/(1-q)} & \text{if }q \ne 1\text{ and }1+(1-q)x \le 0, \\[6pt]
\end{cases}
\]](form_375.png)
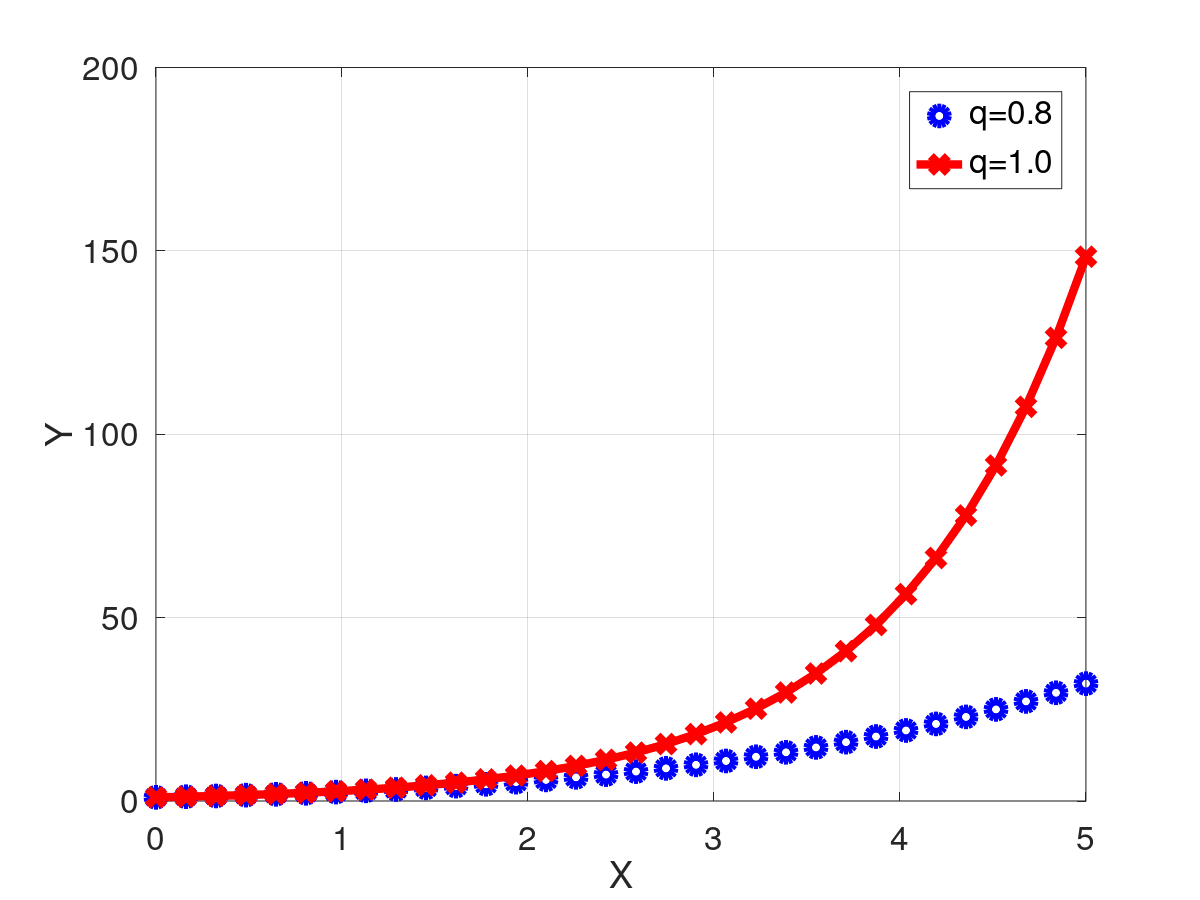
| [in] | x | La variable a evaluar |
| [in] | q | parámetro Tsallis. |
| Pds::Matrix Pds::qExp | ( | const Pds::Matrix & | A, |
| double | q | ||
| ) |
Retorna el resultado de evaluar elemento a elemento la función q-exponent de Tsallis.
![\[
qExp(x) = \begin{cases}
e^{x} & \text{if }q=1, \\[6pt]
[1+(1-q)x]^{1/(1-q)} & \text{if }q \ne 1 \text{ and } 1+(1-q)x >0, \\[6pt]
0^{1/(1-q)} & \text{if }q \ne 1\text{ and }1+(1-q)x \le 0, \\[6pt]
\end{cases}
\]](form_375.png)
![]()

| [in] | A | La matriz a evaluar |
| [in] | q | parámetro Tsallis. |
| double Pds::qLog | ( | double | x, |
| double | q | ||
| ) |
Retorna el resultado de evaluar la función q-logaritmic de Tsallis.
![\[
qLog(x) =
\begin{cases}\ln(x)&{\text{if }}x>0{\text{ and }}q=1\\[8pt]{\dfrac {x^{1-q}-1}{1-q}}&{\text{if }}x>0{\text{ and }}q\neq 1\\[8pt]{\text{Undefined }}&{\text{if }}x\leq 0\\[8pt]\end{cases}
\]](form_377.png)
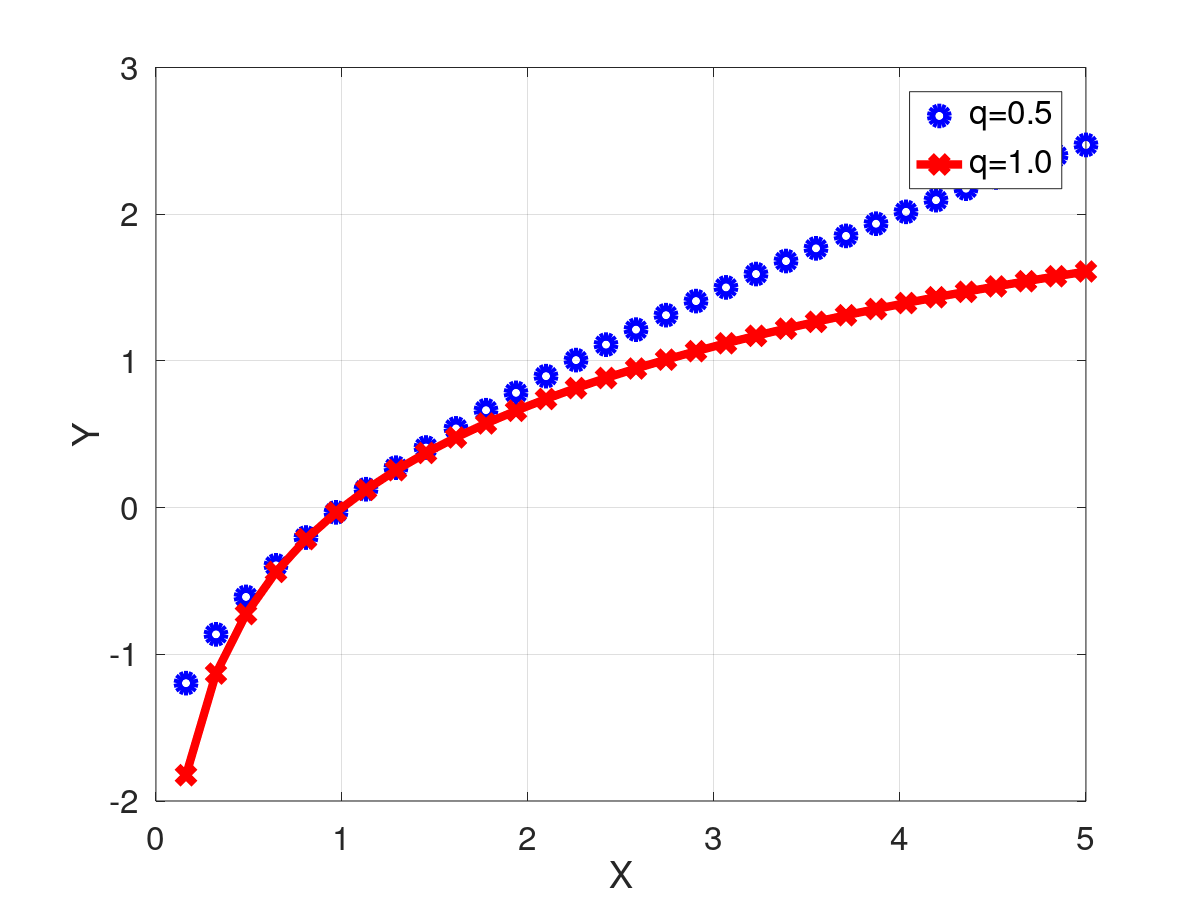
| [in] | x | La variable a evaluar |
| [in] | q | parámetro Tsallis. |
| Pds::Matrix Pds::qLog | ( | const Pds::Matrix & | A, |
| double | q | ||
| ) |
Retorna el resultado de evaluar elemento a elemento la función q-logaritmic de Tsallis.
![\[
qLog(x) =
\begin{cases}\ln(x)&{\text{if }}x>0{\text{ and }}q=1\\[8pt]{\dfrac {x^{1-q}-1}{1-q}}&{\text{if }}x>0{\text{ and }}q\neq 1\\[8pt]{\text{Undefined }}&{\text{if }}x\leq 0\\[8pt]\end{cases}
\]](form_377.png)
![]()

| [in] | A | La matriz a evaluar |
| [in] | q | parámetro Tsallis. |
| double Pds::qHbn | ( | double | x, |
| double | q | ||
| ) |
Retorna el resultado de evaluar la función entropia de Tsallis.
![\[
qHbn(x) = \frac{1-x^{q}-(1-x)^{q}}{q-1}
\]](form_379.png)
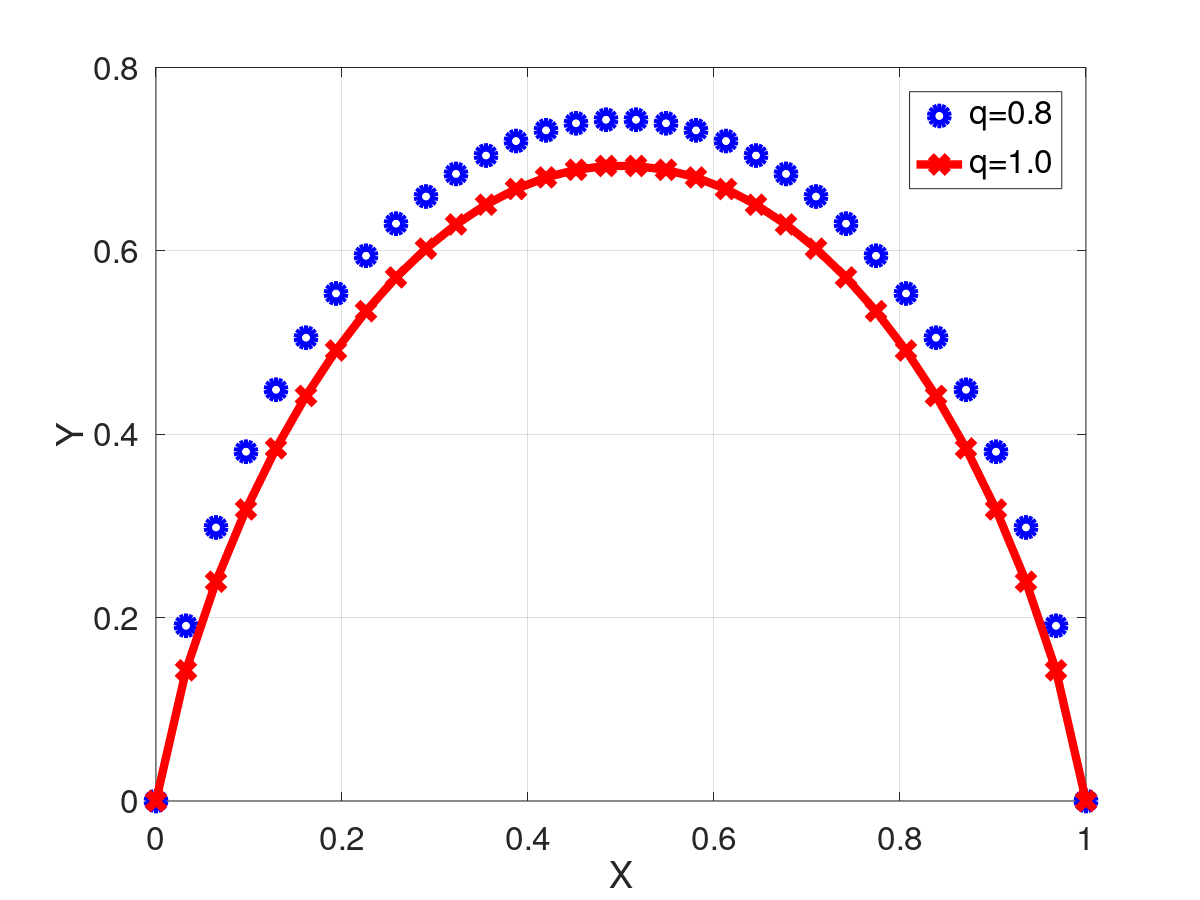
| [in] | x | La variable a evaluar |
| [in] | q | parámetro Tsallis. |
| Pds::Matrix Pds::qHbn | ( | const Pds::Matrix & | A, |
| double | q | ||
| ) |
Retorna el resultado de evaluar elemento a elemento la función entropia de Tsallis.
![\[
qHbn(x) = \frac{1-x^{q}-(1-x)^{q}}{q-1}
\]](form_379.png)
![]()

| [in] | A | La matriz a evaluar |
| [in] | q | parámetro Tsallis. |
| double Pds::qDHbn | ( | double | x, |
| double | q | ||
| ) |
Retorna el resultado de evaluar la derivada de la función entropia de Tsallis.
![\[
qDHbn(x) = \frac{-q~x^{q-1}+q~(1-x)^{q-1}}{q-1}
\]](form_381.png)
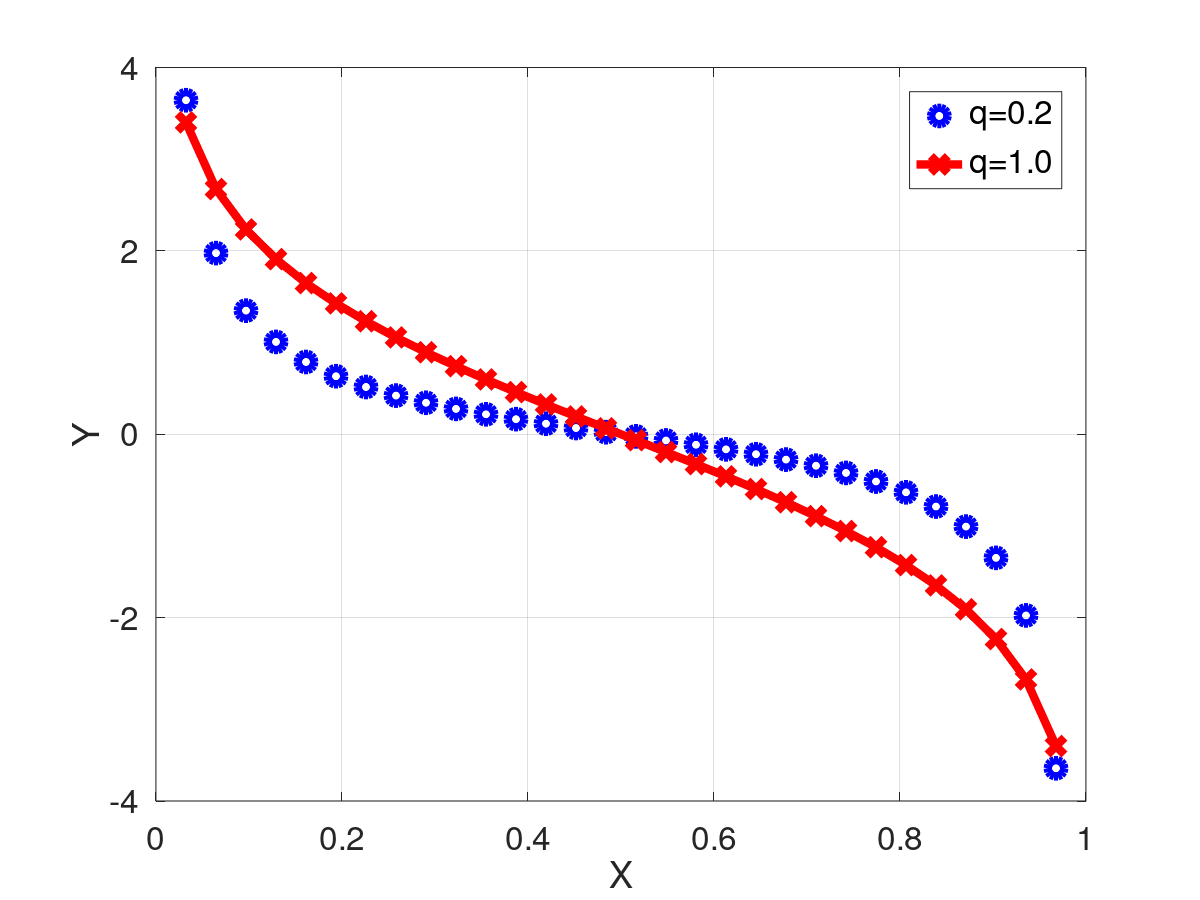
| [in] | x | La variable a evaluar |
| [in] | q | parámetro Tsallis. |
| Pds::Matrix Pds::qDHbn | ( | const Pds::Matrix & | A, |
| double | q | ||
| ) |
Retorna el resultado de evaluar elemento a elemento la derivada función entropia de Tsallis.
![\[
qDHbn(x) = \frac{-q~x^{q-1}+q~(1-x)^{q-1}}{q-1}
\]](form_381.png)
![]()

| [in] | A | La matriz a evaluar |
| [in] | q | parámetro Tsallis. |
| double Pds::InformationGain | ( | const Pds::Matrix & | B, |
| const std::vector< Pds::Matrix > & | A, | ||
| double | Umbral = 0.5 |
||
| ) |
Retorna el Information Gain entre si mismo B y {A[0],A[1],...,A[N-1]}. Antes de comprarar las matrices se binarizan con el umbral Umbral. A[n]>Umbral, B>Umbral.
![]()
![\[IG=h_b(p_{\mathbf{B}})-\sum_{n=0}^{N-1} \frac{N_{\mathbf{A[n]}}}{N_{\mathbf{B}}}h_b(p_{\mathbf{A[n]}})\]](form_384.png)
| [in] | B | Matriz total. Estas seran binarizadas con Umbral. |
| [in] | A | vector de matrices. Estas seran binarizadas con Umbral. |
| [in] | Umbral | Umbral de binarización. A>Umbral. |
| Pds::Vector Pds::InformationGainScale | ( | const Pds::Vector & | Y, |
| double | Umbral = 0.5 |
||
| ) |
Retorna un vector con todos los valores de Information Gain, dependiendo en donde se realice un corte en el vector ![]() .
.
![]()
![\[
IG_{i}=h_b(p_{\mathbf{Y}})
- \frac{i}{N}h_b(p_{\mathbf{Y}_{0:i-1}})
- \frac{N-i}{N}h_b(p_{\mathbf{Y}_{i:N-1}})
\]](form_390.png)
El valor IG.GetRaw(i) es el Information Gain si quiebro el vector ![]() en
en ![]() y
y ![]() , es decir
, es decir ![]()
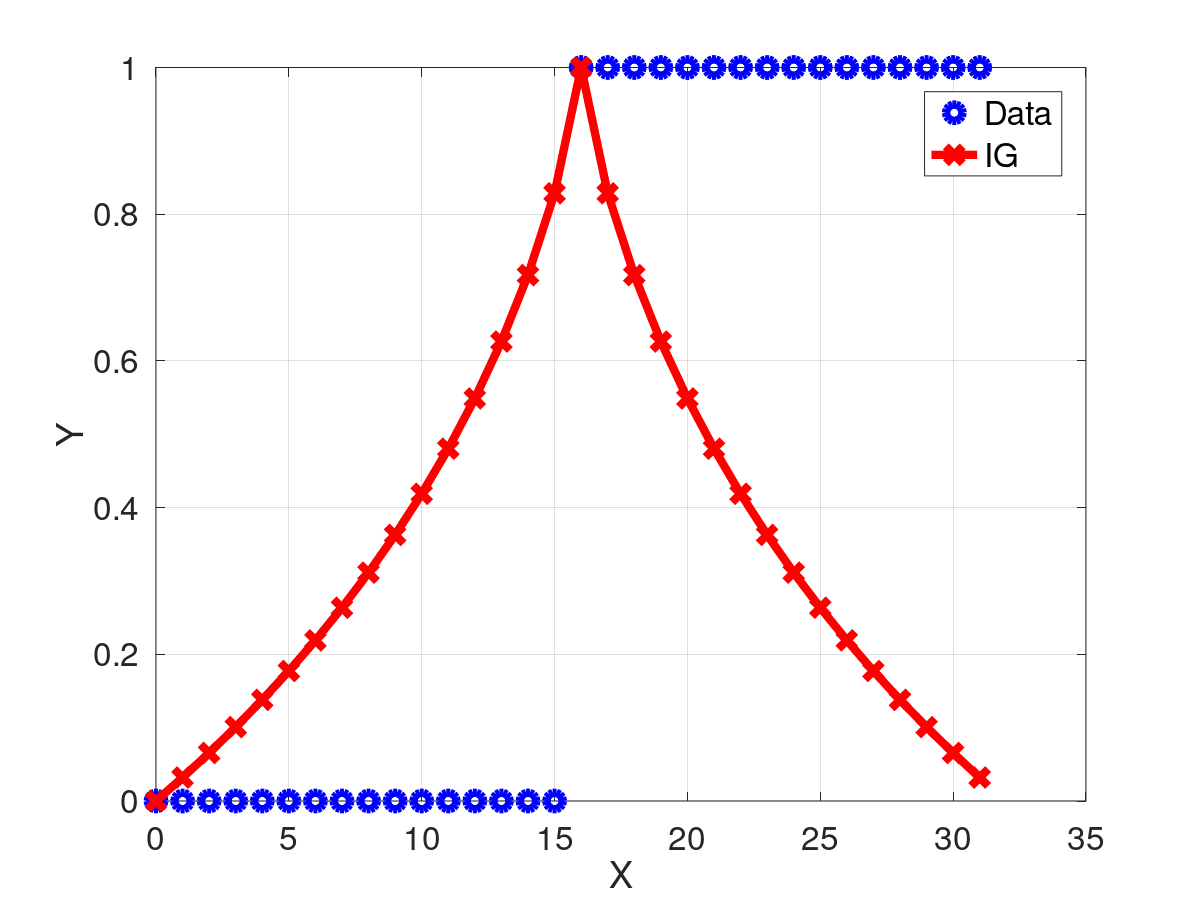
| [in] | Y | Data |
| [in] | Umbral | Umbral de para la binarizacion de |
| Pds::Vector Pds::InformationSumScale | ( | const Pds::Vector & | Y, |
| double | Umbral = 0.5 |
||
| ) |
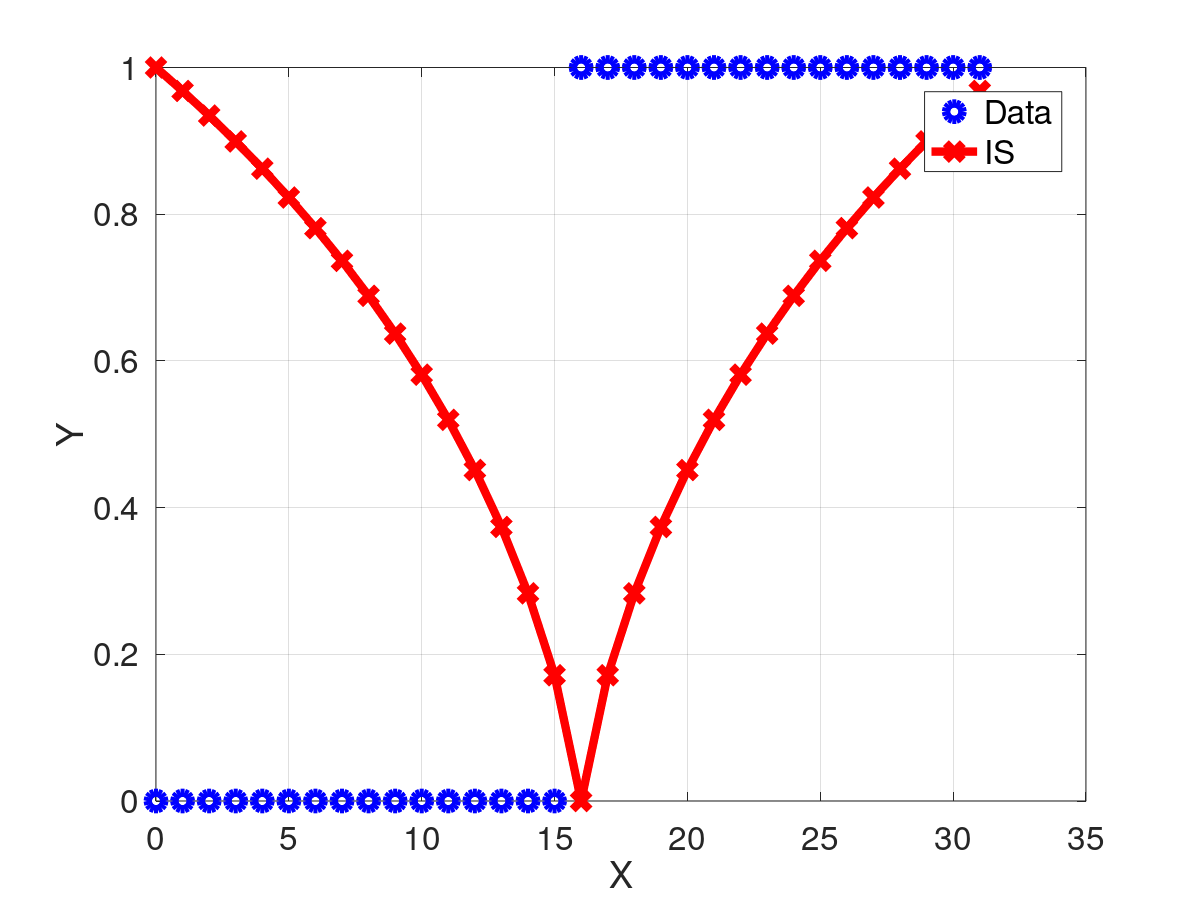
Retorna un vector con todos los valores de Information Sum, dependiendo en donde se realice un corte en el vector ![]() .
.
![]()
![\[
IS_{i}=
\frac{i}{N}h_b(p_{\mathbf{Y}_{0:i-1}})+
\frac{N-i}{N}h_b(p_{\mathbf{Y}_{i:N-1}})
\]](form_399.png)
El valor IS.GetRaw(i) es el Information Sum si quiebro el vector ![]() en
en ![]() y
y ![]() , es decir
, es decir ![]()
| [in] | Y | Data |
| [in] | Umbral | Umbral de para la binarizacion de |
| double Pds::CDF::Phi | ( | double | x | ) |
Calcula el valor de la función ![]() .
.
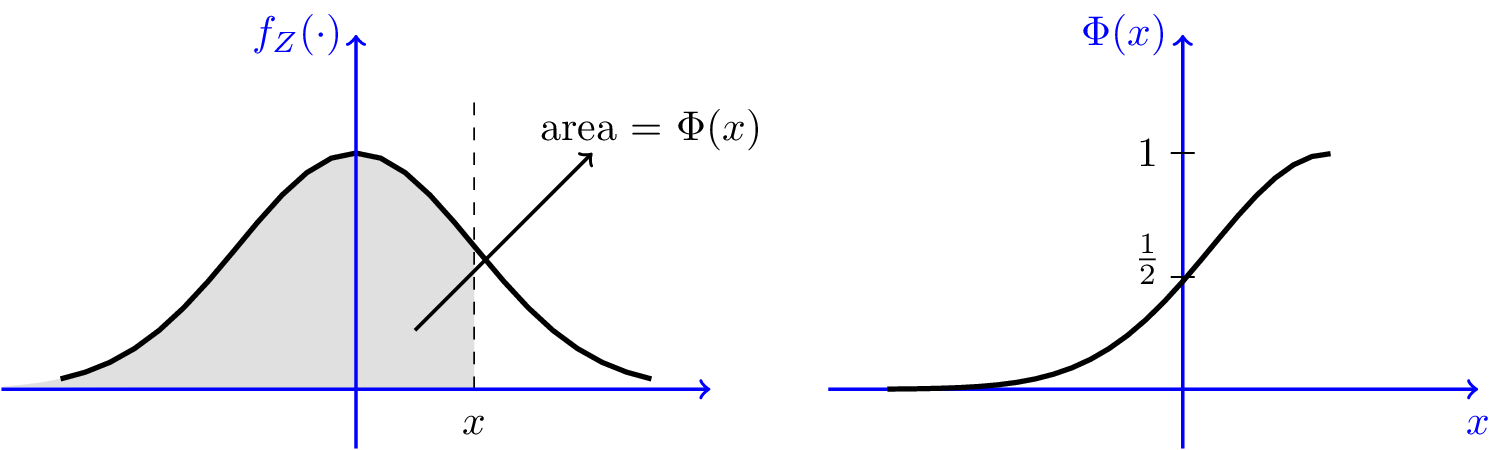
![\[ \Phi(x)={\frac {1}{\sqrt{2\pi}}}\int _{-\infty }^{x}e^{-t^{2}/2}\,dt\]](form_477.png)
![\[ \Phi(x)=\frac{1}{2}\left(1+erf\left(\frac{x}{\sqrt{2}}\right) \right)\]](form_478.png)
| [in] | x | Valor a evaluar. |
| double Pds::CDF::Phi | ( | double | x, |
| double | mu, | ||
| double | sigma | ||
| ) |
Calcula el valor de la función ![]() .
.

![\[ \Phi(x; \mu,\sigma)=\frac{1}{2}\left(1+erf\left(\frac{x-\mu}{\sigma \sqrt{2}}\right) \right)\]](form_479.png)
| [in] | x | Valor a evaluar. |
| [in] | mu | Valor medio |
| [in] | sigma | Valor del desvio padrón |
| Pds::Matrix Pds::CDF::Phi | ( | const Pds::Matrix & | A | ) |
Calcula el valor de la función ![]() .
.

![\[ \Phi(x)={\frac {1}{\sqrt{2\pi}}}\int _{-\infty }^{x}e^{-t^{2}/2}\,dt\]](form_477.png)
![\[ \Phi(x)=\frac{1}{2}\left(1+erf\left(\frac{x}{\sqrt{2}}\right) \right)\]](form_478.png)
![]()
| [in] | A | Matriz a procesar. |
| double Pds::CDF::Probit | ( | double | p | ) |
Calcula el valor de la función ![]() que es la inversa de
que es la inversa de ![]() Pds::CDF::Phi().
Pds::CDF::Phi().
![\[ p=\Phi(x)={\frac {1}{\sqrt{2\pi}}}\int _{-\infty }^{x}e^{-t^{2}/2}\,dt\]](form_484.png)
![]()
| [in] | p | La variable a evaluar |
| Pds::Matrix Pds::CDF::Probit | ( | const Pds::Matrix & | A | ) |
Calcula el valor de la función ![]() que es la inversa de
que es la inversa de ![]() Pds::CDF::Phi().
Pds::CDF::Phi().
![\[ p=\Phi(x)={\frac {1}{\sqrt{2\pi}}}\int _{-\infty }^{x}e^{-t^{2}/2}\,dt\]](form_484.png)
![]()
| [in] | A | Matriz a procesar. |
| double Pds::Var | ( | const Pds::Matrix & | A, |
| double * | mean | ||
| ) |
Calcula el valor de la varianza de la matriz A.
| [in] | A | Matriz a procesar. |
| [in] | mean | Valor medio de los elelento de la Matriz A. |
| double Pds::Var | ( | const Pds::Matrix & | A | ) |
Calcula el valor de la varianza de la matriz A.
| [in] | A | Matriz a procesar. |
| double Pds::Mean | ( | const Pds::Matrix & | A | ) |
Calcula el valor medio de los elementos de la matriz A.
| [in] | A | Matriz a procesar. |
| double Pds::Sum | ( | const Pds::Matrix & | A | ) |
Calcula el valor de la suma de los elementos de la matriz A.
| [in] | A | Matriz a procesar. |
| double Pds::R2 | ( | const Pds::Matrix & | A, |
| const Pds::Matrix & | B | ||
| ) |
Calcula el coeficiente de determinación o ![]() .
.
![\[ R^2\equiv R2(A,B)\quad =\quad 1-\frac{\sigma_r^2}{\sigma^2}\quad =\quad 1-\frac{\frac{1}{L}|| \mathbf{A}_{ij}-\mathbf{B}_{ij}||^2}{Var(\mathbf{A})}\]](form_403.png)
![]()
Varianza ![]() , varianza residual
, varianza residual ![]() .
.
| double Pds::Accuracy | ( | const Pds::Matrix & | A, |
| const Pds::Matrix & | B, | ||
| double | Umbral = 0.5 |
||
| ) |
Calcula el valor de la Accuracy entre los elementos de las matrices A y B. A>Umbral, B>Umbral.
![\[Accuracy=\frac{TP+TN}{TP+TN+FP+FN}=\frac{Number~of~A==B}{Number~of~elements~in~A}\]](form_407.png)
TP=True positive TN=True negative FP=False positive FN=False negative
| [in] | A | Matriz a procesar. |
| [in] | B | Matriz a procesar. |
| [in] | Umbral | Umbral de binarización. |
| double Pds::AccuracyBatchBlock | ( | const Pds::BatchBlock & | A, |
| const Pds::BatchBlock & | B, | ||
| double | Umbral = 0.5 |
||
| ) |
Calcula el valor de la Accuracy entre los elementos de las matrices A y B. A>Umbral, B>Umbral.
![\[Accuracy=\frac{TP+TN}{TP+TN+FP+FN}=\frac{Number~of~A==B}{Number~of~elements~in~A}\]](form_407.png)
TP=True positive TN=True negative FP=False positive FN=False negative
| [in] | A | Vector de SampleBlock a procesar. |
| [in] | B | Vector de SampleBlock a procesar. |
| [in] | Umbral | Umbral de binarización. |
| bool Pds::CountRoundEqualIn | ( | const Pds::Matrix & | A, |
| const Pds::Matrix & | B, | ||
| unsigned int & | S, | ||
| unsigned int & | T | ||
| ) |
Calcula el número de elementos enteros iguales entre las matrices A y B.
![]()
| [in] | A | Matriz a procesar. |
| [in] | B | Matriz a procesar. |
| [out] | S | Número de elementos iguales. |
| [out] | T | Número total de elementos. |
| bool Pds::CountRoundEqualInBatchBlock | ( | const Pds::BatchBlock & | A, |
| const Pds::BatchBlock & | B, | ||
| unsigned int & | S, | ||
| unsigned int & | T | ||
| ) |
| bool Pds::SquareErrorInBatchBlock | ( | const Pds::BatchBlock & | A, |
| const Pds::BatchBlock & | B, | ||
| double & | S | ||
| ) |
| double Pds::NAccuracy | ( | const Pds::Matrix & | A, |
| const Pds::Matrix & | B | ||
| ) |
Calcula el valor de la Accuracy entre los elementos de las matrices A y B. round(A), round(B).
![\[Accuracy=\frac{Number~of~A==B}{Number~of~elements~in~A}\]](form_410.png)
| [in] | A | Matriz a procesar. |
| [in] | B | Matriz a procesar. |
| double Pds::MeanAbsoluteError | ( | const Pds::Matrix & | A, |
| const Pds::Matrix & | B | ||
| ) |
Calcula el valor del error absoluto medio.
![\[ Pds::MeanAbsoluteError(A,B)=\frac{1}{Nlin~Ncol}\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}-b_{ij}|} \]](form_411.png)
| [in] | A | Matriz a procesar. |
| [in] | B | Matriz a procesar. |
| double Pds::ArgMax | ( | const Pds::Matrix & | X | ) |
Retorna el identicador (ID) de la posicion del máximo en la matriz. En caso de existir varios máximos la función retorna el primero en ser encontrado.
![]()
| [in] | X | El vector de entrada. |
| double Pds::ArgMin | ( | const Pds::Matrix & | X | ) |
Retorna el identicador (ID) de la posicion del mínimo en la matriz. En caso de existir varios mínimos la función retorna el primero en ser encontrado.
![]()
| [in] | X | El vector de entrada. |
| double Pds::Det | ( | const Pds::Matrix & | A | ) |
Calcula el valor de la detrminante de una matriz.
![]()
| [in] | A | El vector de entrada. |
| double Pds::RMS | ( | const Pds::Matrix & | A | ) |
Calcula el valor raiz quadrático medio de una matriz.
![\[ Pds::RMS(A)=\sqrt{\frac{1}{Nlin~Ncol}\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}|}^2} \]](form_416.png)
| [in] | A | El vector de entrada. |
| double Pds::MeanAbsolute | ( | const Pds::Matrix & | A | ) |
Calcula el valor absoluto medio de una matriz.
![\[ Pds::MeanSquare(A)=\frac{1}{Nlin~Ncol}\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}|} \]](form_417.png)
| [in] | A | El vector de entrada. |
| double Pds::MeanSquare | ( | const Pds::Matrix & | A | ) |
Calcula el valor quadrático medio de una matriz.
![\[ Pds::MeanSquare(A)=\frac{1}{Nlin~Ncol}\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}|}^2 \]](form_418.png)
| [in] | A | El vector de entrada. |
| double Pds::SumSquare | ( | const Pds::Matrix & | A | ) |
Calcula el valor de la suma quadrática de una matriz.
![\[ Pds::SumSquare(A)=\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}|}^2 \]](form_419.png)
| [in] | A | El vector de entrada. |
| double Pds::Norm | ( | const Pds::Matrix & | A | ) |
Calcula el valor dela norma (Frobenius) de una matriz.
![\[ Pds::Norm(A)=\sqrt{\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}|}^2} \]](form_420.png)
| [in] | A | El vector de entrada. |
| double Pds::NormDiff | ( | const Pds::Matrix & | A, |
| const Pds::Matrix & | B | ||
| ) |
Calcula el valor dela norma (Frobenius) de una matriz.
![\[ Pds::Norm(A,B)=\sqrt{\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}-b_{ij}|}^2} \]](form_421.png)
| [in] | A | El vector de entrada. |
| [in] | B | El vector de entrada. |
| Pds::Matrix Pds::SQNL | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la función SQNL.
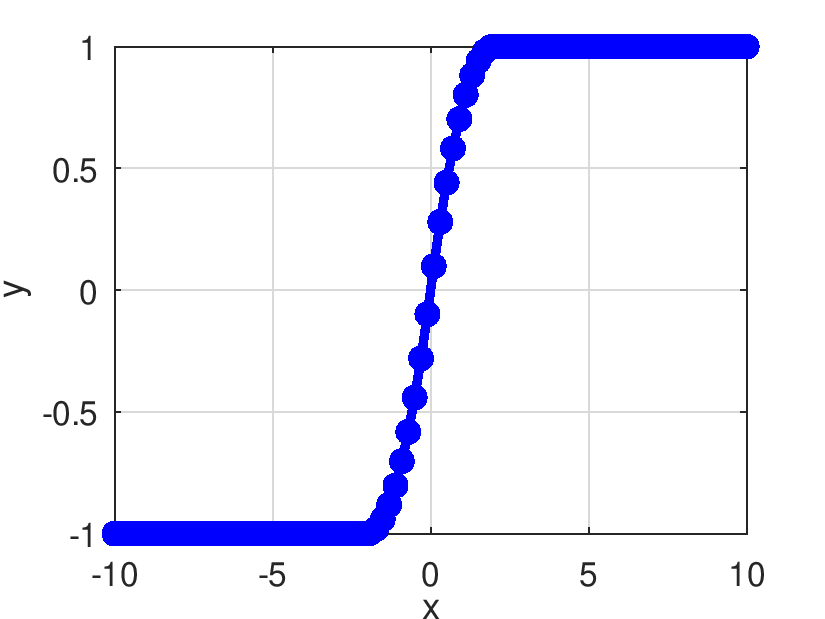
![\[
Pds::SQNL(x)=
\left\{
\begin{matrix}
+1 & if & 2<x \\
x-\frac{x^2}{4} & if & 0\leq x\leq 2 \\
x+\frac{x^2}{4} & if & -2 \leq x< 0 \\
-1 & if & x<-2
\end{matrix}
\right.
\]](form_422.png)
| [in] | X | La matriz a evaluar |
| double Pds::SQNL | ( | double | x | ) |
Retorna el resultado de evaluar la función SQNL.

![\[
Pds::SQNL(x)=
\left\{
\begin{matrix}
+1 & if & 2<x \\
x-\frac{x^2}{4} & if & 0\leq x\leq 2 \\
x+\frac{x^2}{4} & if & -2 \leq x< 0 \\
-1 & if & x<-2
\end{matrix}
\right.
\]](form_422.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::DSQNL | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la derivada de la función SQNL.
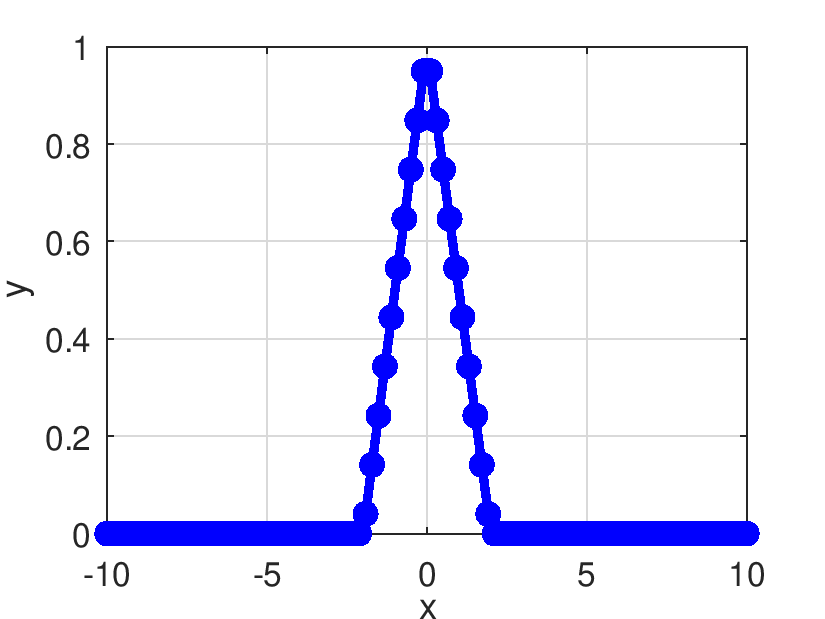
![\[
\frac{\partial Pds::SQNL(x)}{\partial x}=
\left\{
\begin{matrix}
0 & if & 2<x \\
1-\frac{x}{2} & if & 0\leq x\leq 2\\
1+\frac{x}{2} & if & -2 \leq x< 0 \\
0 & if & x<-2
\end{matrix}
\right.
\]](form_423.png)
| [in] | X | La matriz a evaluar |
| double Pds::DSQNL | ( | double | x | ) |
Retorna el resultado de evaluar la derivada de la función SQNL.

![\[
\frac{\partial Pds::SQNL(x)}{\partial x}=
\left\{
\begin{matrix}
0 & if & 2<x \\
1-\frac{x}{2} & if & 0\leq x\leq 2\\
1+\frac{x}{2} & if & -2 \leq x< 0 \\
0 & if & x<-2
\end{matrix}
\right.
\]](form_423.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::Identity | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la función linear.
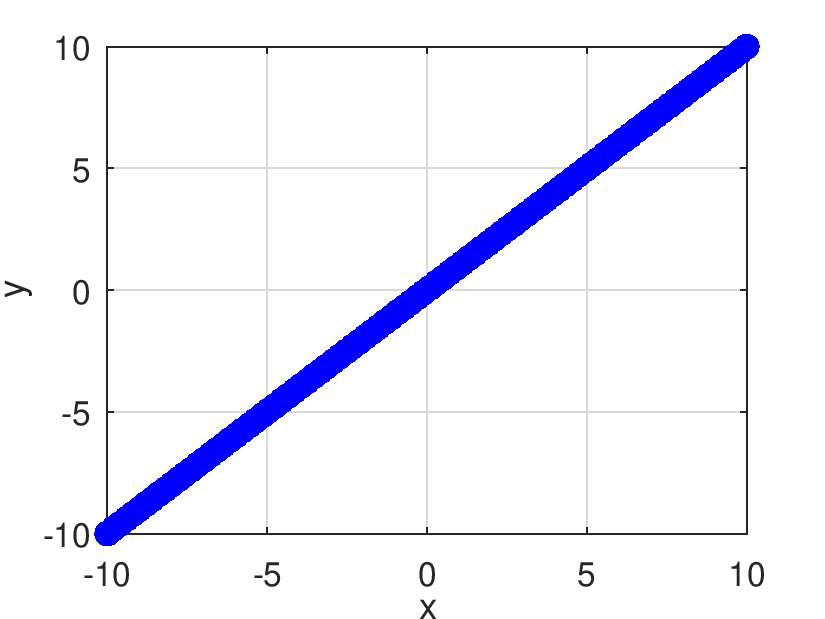
![]()
| [in] | X | La matriz a evaluar |
| double Pds::Identity | ( | double | x | ) |
Retorna el resultado de evaluar la función linear.

![]()
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::DIdentity | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la derivada de la función linear.
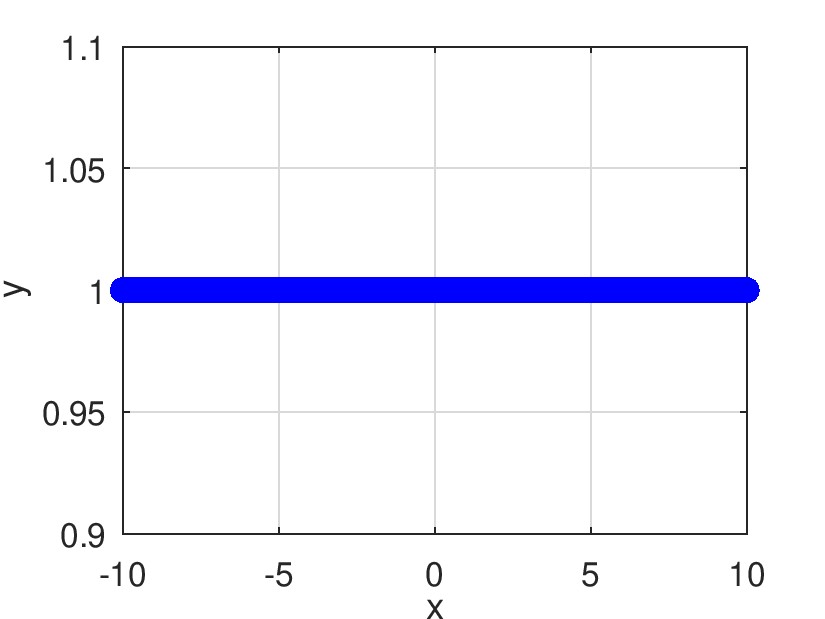
![\[ \frac{\partial Pds::Identity(x)}{\partial x}=1 \]](form_425.png)
| [in] | X | La matriz a evaluar |
| double Pds::DIdentity | ( | double | x | ) |
Retorna el resultado de evaluar la derivada de la función linear.

![\[ \frac{\partial Pds::Identity(x)}{\partial x}=1 \]](form_425.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::SoftSign | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la función SoftSign.
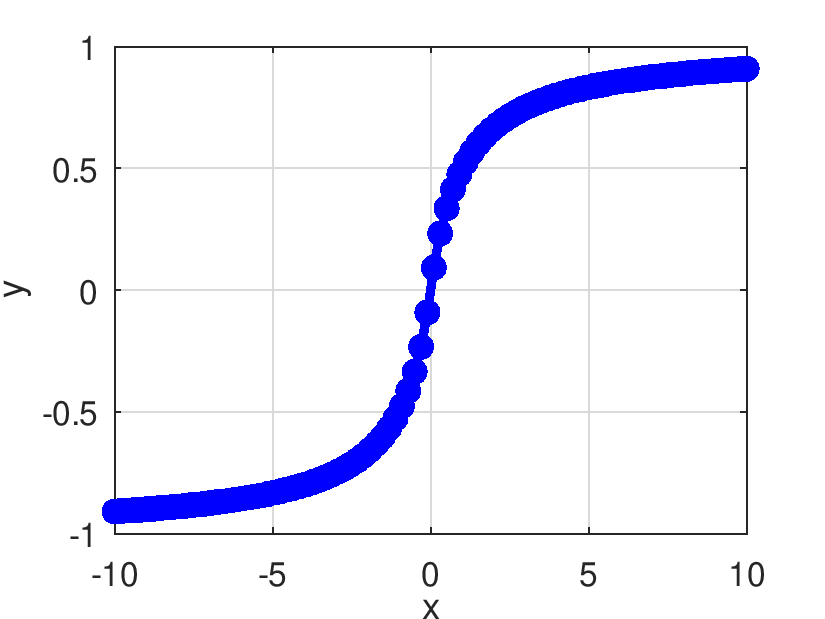
![\[
Pds::SoftSign(x)=\frac{x}{1+|x|}
\]](form_426.png)
| [in] | X | La matriz a evaluar |
| double Pds::SoftSign | ( | double | x | ) |
Retorna el resultado de evaluar la función SoftSign.

![\[
Pds::SoftSign(x)=\frac{x}{1+|x|}
\]](form_426.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::DSoftSign | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la derivada de la función SoftSign.
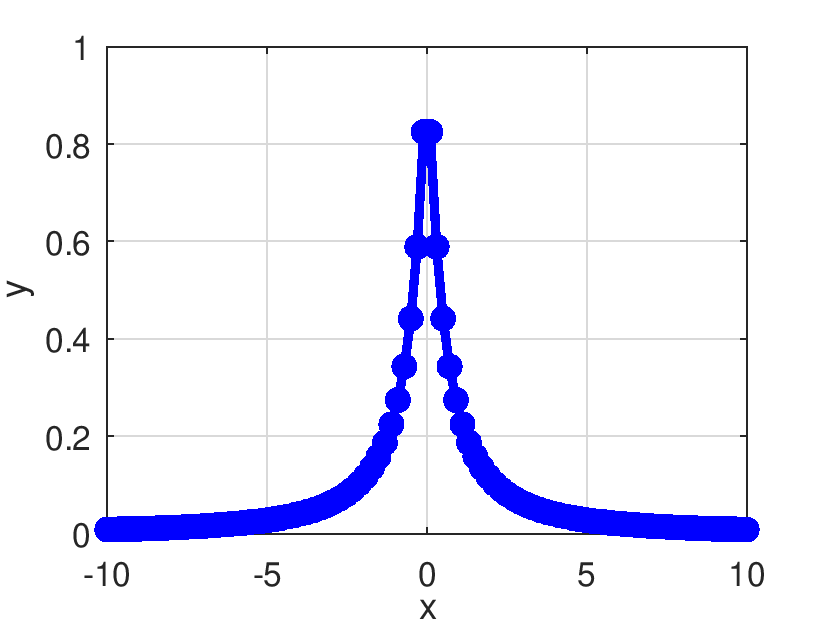
![\[
Pds::SoftSign(x)=\frac{1}{(1+|x|)^2}
\]](form_427.png)
| [in] | X | La matriz a evaluar |
| double Pds::DSoftSign | ( | double | x | ) |
Retorna el resultado de evaluar la derivada de la función SoftSign.

![\[
Pds::SoftSign(x)=\frac{1}{(1+|x|)^2}
\]](form_427.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::ELU | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la función ELU.
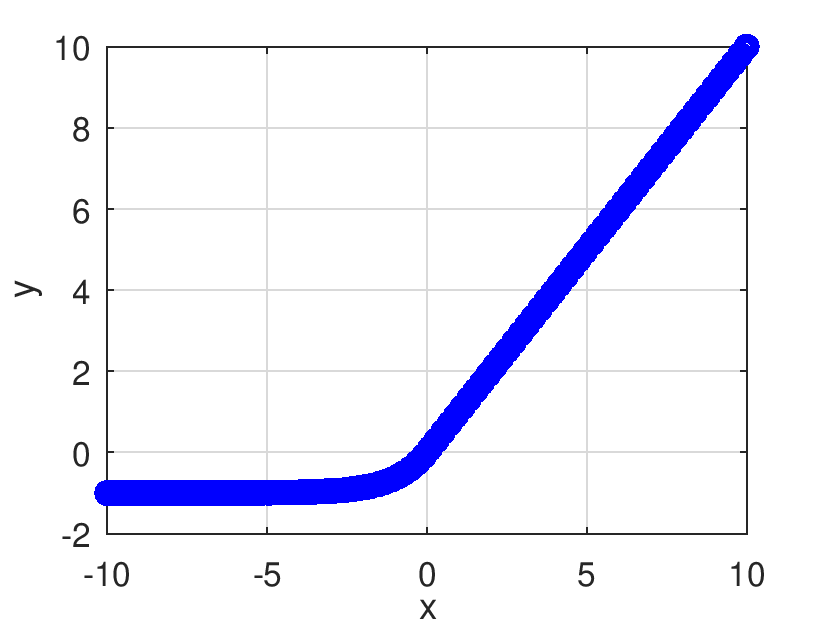
![\[
Pds::ELU(x)=
\left\{
\begin{matrix}
x & if & x > 0 \\
e^{x}-1 & if & x\leq 0
\end{matrix}
\right.
\]](form_428.png)
| [in] | X | La matriz a evaluar |
| double Pds::ELU | ( | double | x | ) |
Retorna el resultado de evaluar la función ELU.

![\[
Pds::ELU(x)=
\left\{
\begin{matrix}
x & if & x > 0 \\
e^{x}-1 & if & x\leq 0
\end{matrix}
\right.
\]](form_428.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::DELU | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la derivada de la función ELU.
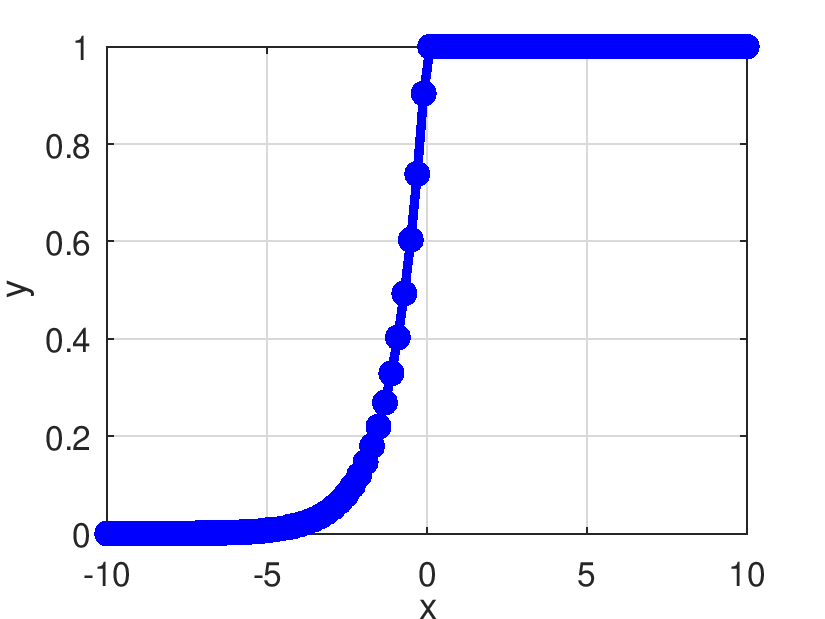
![\[
Pds::DELU(x)=
\left\{
\begin{matrix}
1 & if & x > 0 \\
e^{x} & if & x\leq 0
\end{matrix}
\right.
\]](form_429.png)
| [in] | X | La matriz a evaluar |
| double Pds::DELU | ( | double | x | ) |
Retorna el resultado de evaluar la derivada de la función ELU.

![\[
Pds::DELU(x)=
\left\{
\begin{matrix}
1 & if & x > 0 \\
e^{x} & if & x\leq 0
\end{matrix}
\right.
\]](form_429.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::SoftPlus | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la función SoftPlus.
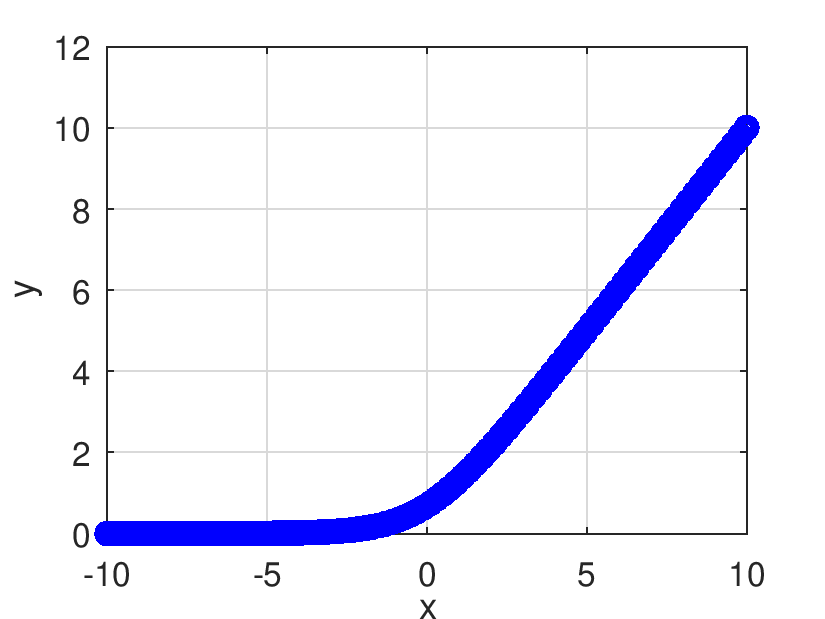
![]()
| [in] | X | La matriz a evaluar |
| double Pds::SoftPlus | ( | double | x | ) |
Retorna el resultado de evaluar la función SoftPlus.

![]()
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::DSoftPlus | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la derivada de la función SoftPlus.
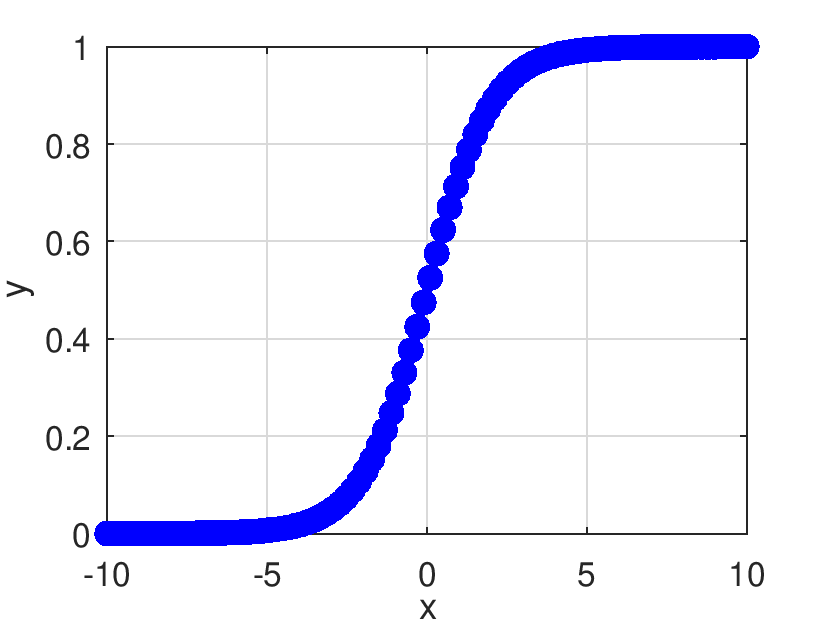
![\[
Pds::DSoftPlus(x)=\frac{1}{1+e^{-x}}
\]](form_431.png)
| [in] | X | La matriz a evaluar |
| double Pds::DSoftPlus | ( | double | x | ) |
Retorna el resultado de evaluar la derivada de la función SoftPlus.

![\[
Pds::DSoftPlus(x)=\frac{1}{1+e^{-x}}
\]](form_431.png)
| [in] | x | La variable a evaluar |
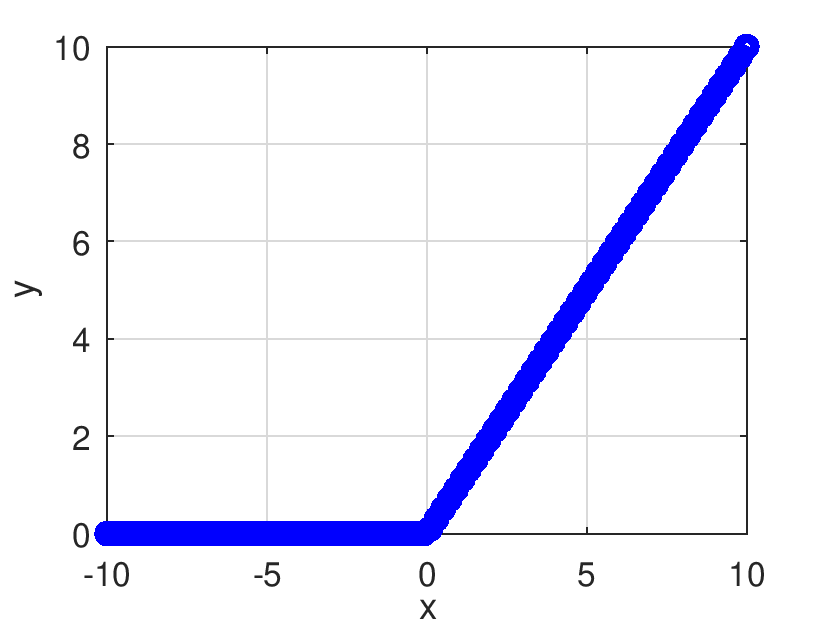
| Pds::Matrix Pds::ReLU | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la función ReLU.
![\[
Pds::ReLU(x)=
\left\{
\begin{matrix}
x & if & x \geq 0 \\
0 & if & x<0
\end{matrix}
\right.
=
std::max(0,x)
\]](form_432.png)
| [in] | X | La matriz a evaluar |
| double Pds::ReLU | ( | double | x | ) |
Retorna el resultado de evaluar la función ReLU.

![\[
Pds::ReLU(x)=
\left\{
\begin{matrix}
x & if & x \geq 0 \\
0 & if & x<0
\end{matrix}
\right.
=
std::max(0,x)
\]](form_432.png)
| [in] | x | La variable a evaluar |
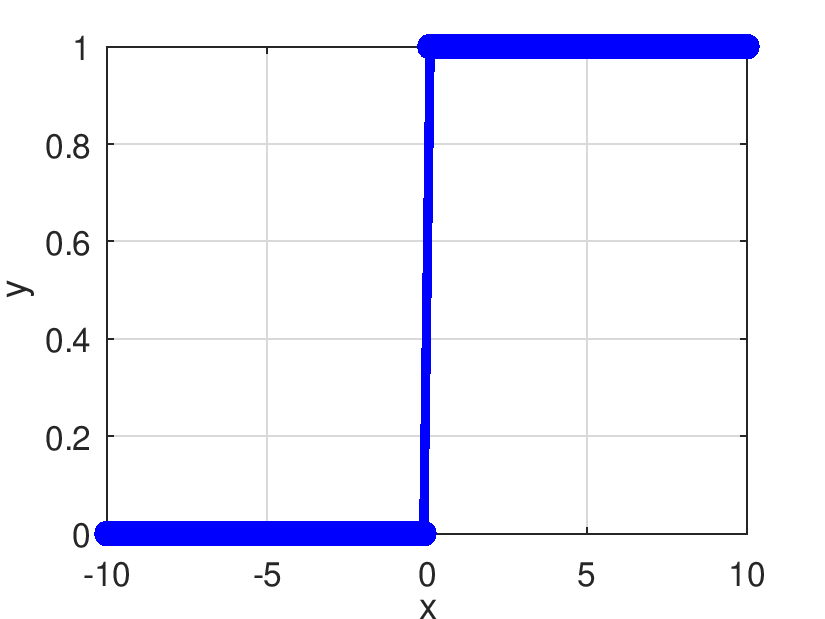
| Pds::Matrix Pds::DReLU | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la derivada de la función ReLU.
![\[
Pds::DReLU(x)=
\left\{
\begin{matrix}
1 & if & x > 0 \\
1 & if & x = 0 \\
0 & if & x < 0
\end{matrix}
\right.
\]](form_433.png)
| [in] | X | La matriz a evaluar |
| double Pds::DReLU | ( | double | x | ) |
Retorna el resultado de evaluar la derivada de la función ReLU.

![\[
Pds::DReLU(x)=
\left\{
\begin{matrix}
1 & if & x > 0 \\
1 & if & x = 0 \\
0 & if & x < 0
\end{matrix}
\right.
\]](form_433.png)
| [in] | x | La variable a evaluar |
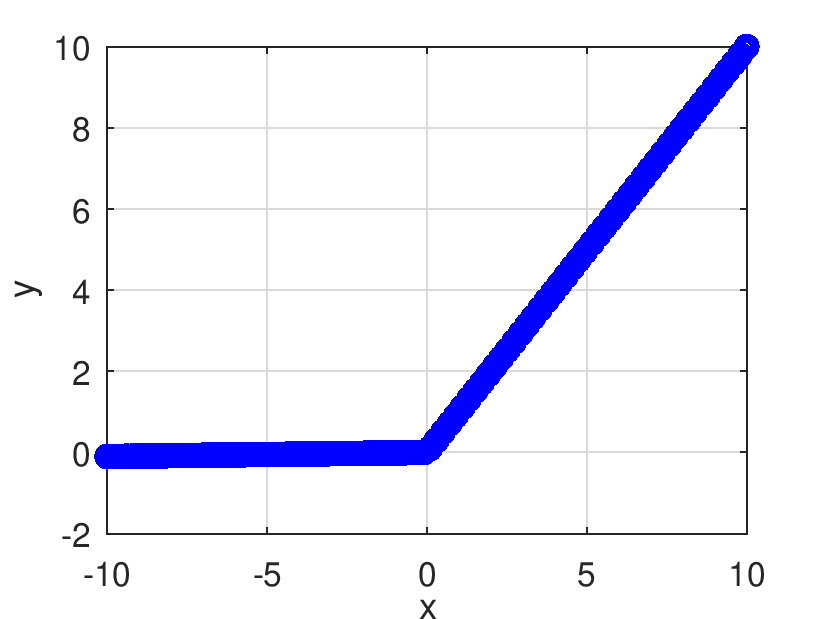
| Pds::Matrix Pds::LeakyReLU | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la función ReLU.
![\[
Pds::LeakyReLU(x)=
\left\{
\begin{matrix}
x & if & x \geq 0 \\
0.01~x & if & x<0
\end{matrix}
\right.
\]](form_434.png)
| [in] | X | La matriz a evaluar |
| double Pds::LeakyReLU | ( | double | x | ) |
Retorna el resultado de evaluar la función Leaky ReLU.

![\[
Pds::LeakyReLU(x)=
\left\{
\begin{matrix}
x & if & x \geq 0 \\
0.01~x & if & x<0
\end{matrix}
\right.
\]](form_434.png)
| [in] | x | La variable a evaluar |
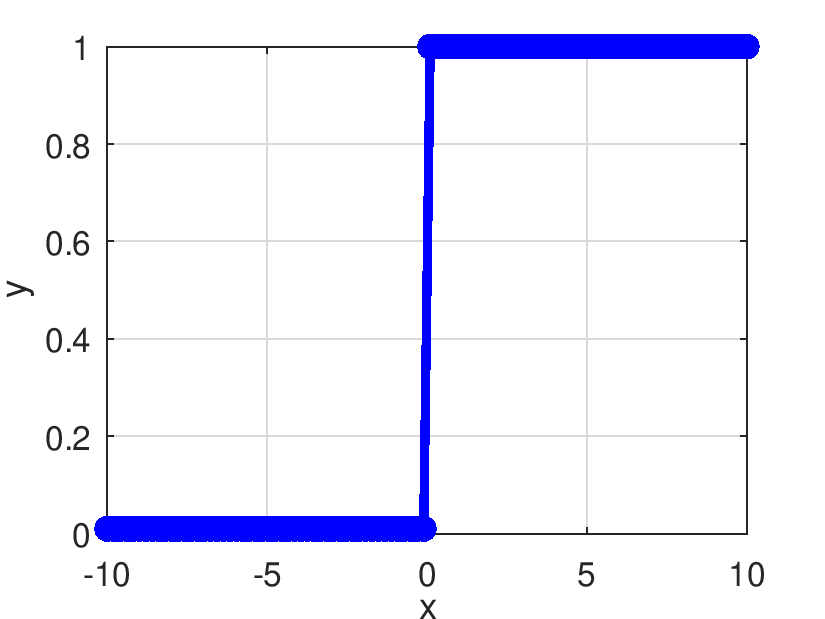
| Pds::Matrix Pds::DLeakyReLU | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la derivada de la función ReLU.
![\[
Pds::DLeakyReLU(x)=
\left\{
\begin{matrix}
1 & if & x \geq 0 \\
0.01 & if & x<0
\end{matrix}
\right.
\]](form_435.png)
| [in] | X | La matriz a evaluar |
| double Pds::DLeakyReLU | ( | double | x | ) |
Retorna el resultado de evaluar la derivada de la función Leaky ReLU.

![\[
Pds::DLeakyReLU(x)=
\left\{
\begin{matrix}
1 & if & x \geq 0 \\
0.01 & if & x<0
\end{matrix}
\right.
\]](form_435.png)
| [in] | x | La variable a evaluar |
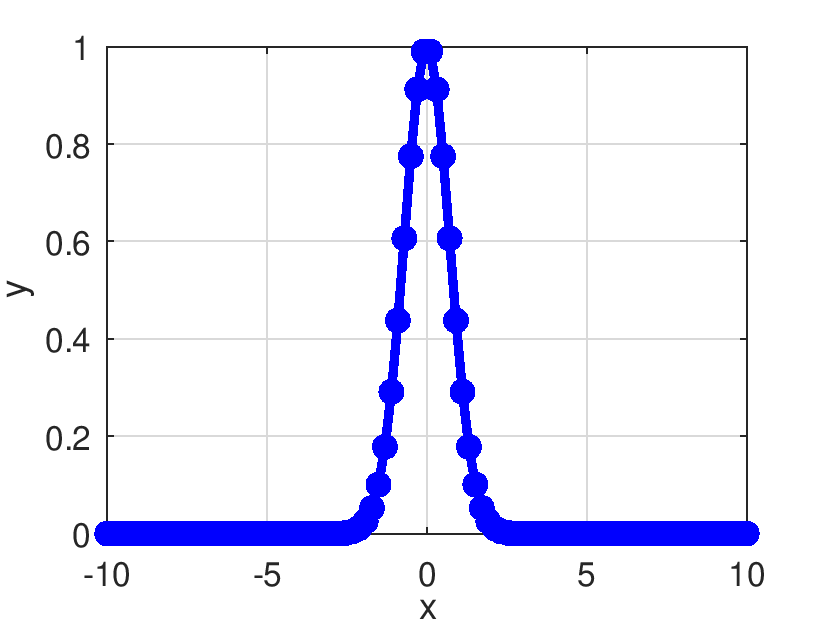
| Pds::Matrix Pds::Gaussian | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la función gaussiana.
![]()
| [in] | X | La matriz a evaluar |
| double Pds::Gaussian | ( | double | x | ) |
Retorna el resultado de evaluar la función gaussiana.

![]()
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::DGaussian | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar la función gaussiana.
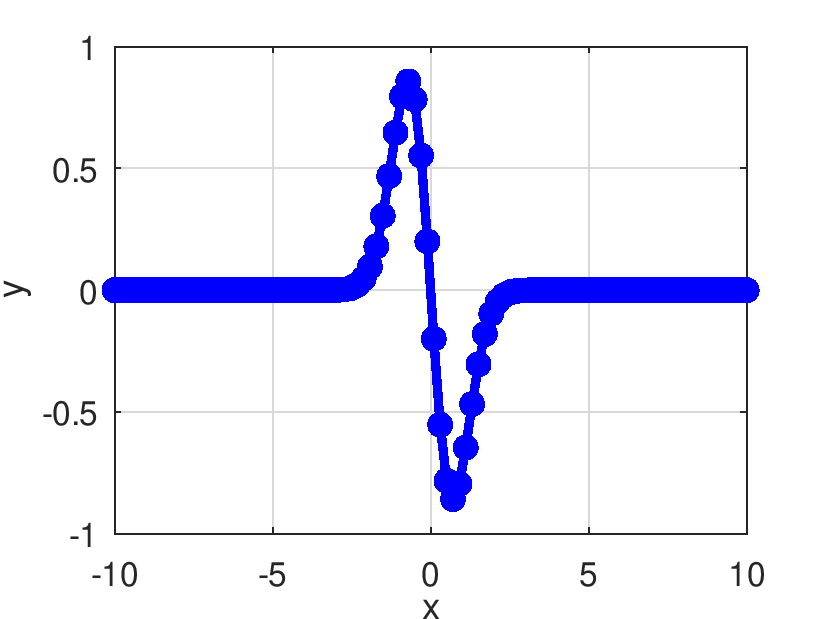
![\[ \frac{\partial Pds::Gaussian(x)}{\partial x}=-2 x e^{-x^2} \]](form_437.png)
| [in] | X | La matriz a evaluar |
| double Pds::DGaussian | ( | double | x | ) |
Retorna el resultado de evaluar la función gaussiana.

![\[ \frac{\partial Pds::Gaussian(x)}{\partial x}=-2 x e^{-x^2} \]](form_437.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::Tanh | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la función tangente hiperbólico.
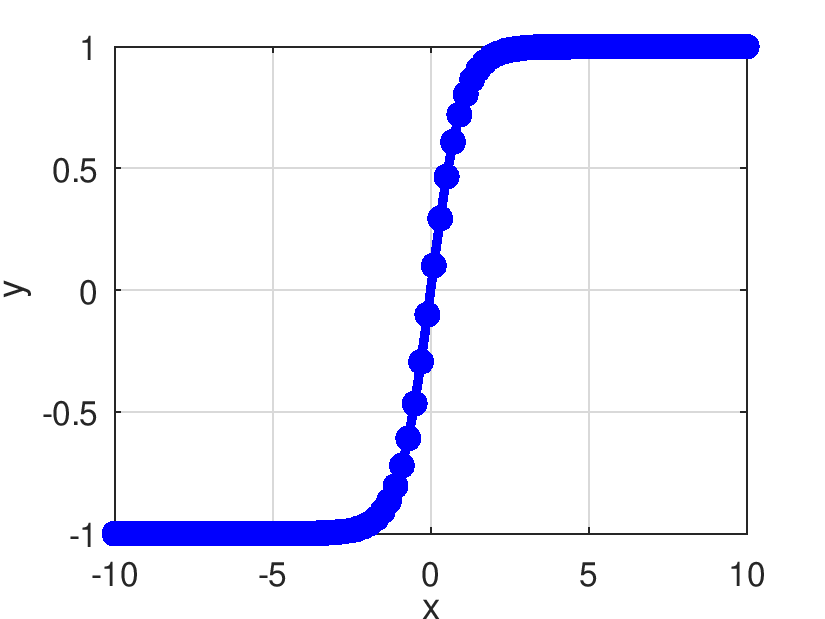
![\[ Pds::Tanh(x)=\frac{e^{2x}-1}{e^{2x}+1} \]](form_438.png)
| [in] | X | La matriz a evaluar |
| double Pds::Tanh | ( | double | x | ) |
Retorna el resultado de evaluar la función tangente hiperbólico.

![\[ Pds::Tanh(x)=\frac{e^{2x}-1}{e^{2x}+1} \]](form_438.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::DTanh | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar la derivada de la función tangente hiperbólico.
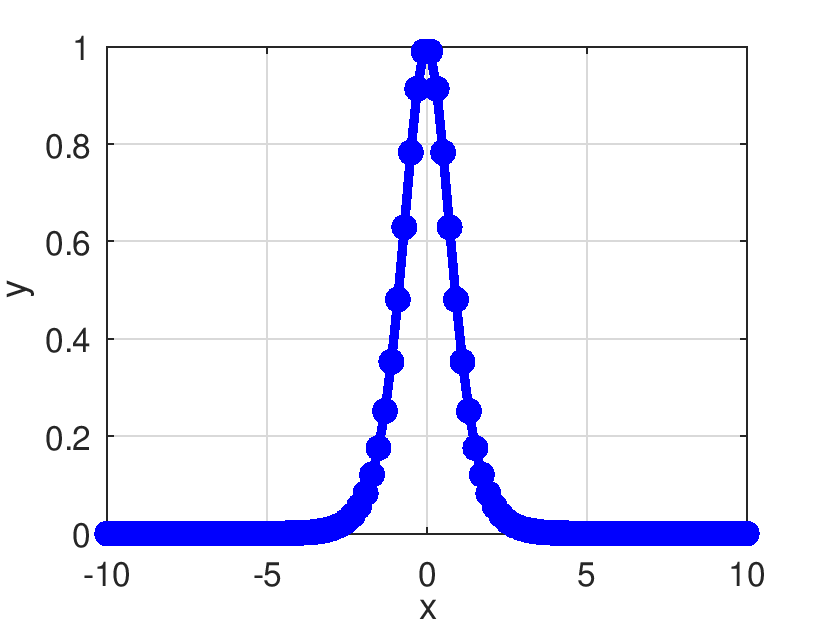
![\[ \frac{\partial Pds::Tanh(x)}{\partial x}=\frac{4 e^{2x}}{(e^{2x}+1)^2} \]](form_439.png)
| [in] | X | La matriz a evaluar |
| double Pds::DTanh | ( | double | x | ) |
Retorna el resultado de evaluar la derivada de la función tangente hiperbólico.

![\[ \frac{\partial Pds::Tanh(x)}{\partial x}=\frac{4 e^{2x}}{(e^{2x}+1)^2} \]](form_439.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::Sigmoid | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la función sigmoid.
![\[ Pds::Sigmoid(x)=\frac{1}{1+e^{-x}} \]](form_440.png)
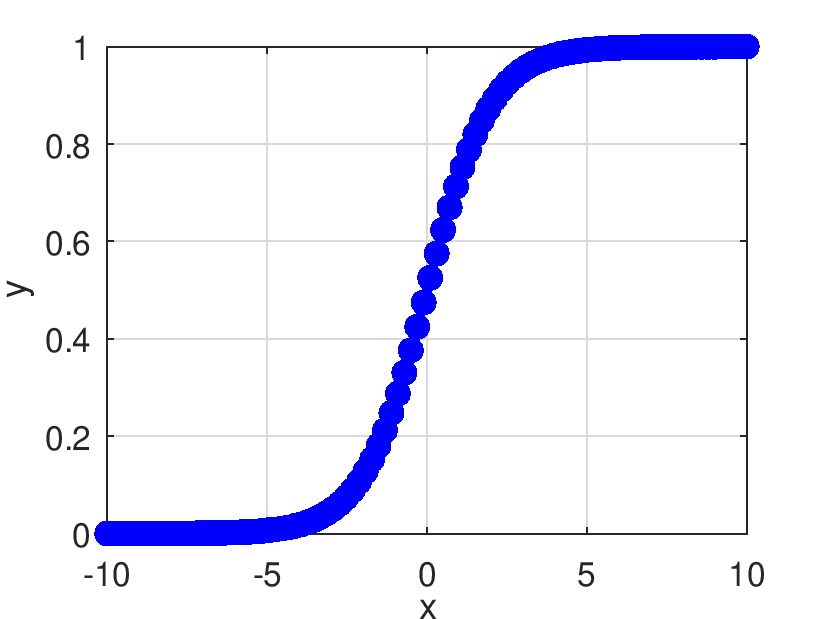
| [in] | X | La matriz a evaluar |
| double Pds::Sigmoid | ( | double | x | ) |
Retorna el resultado de evaluar elemento a elemento la función sigmoid.

![\[ Pds::Sigmoid(x)=\frac{1}{1+e^{-x}} \]](form_440.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::DSigmoid | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar elemento a elemento la derivada de la función sigmoid.
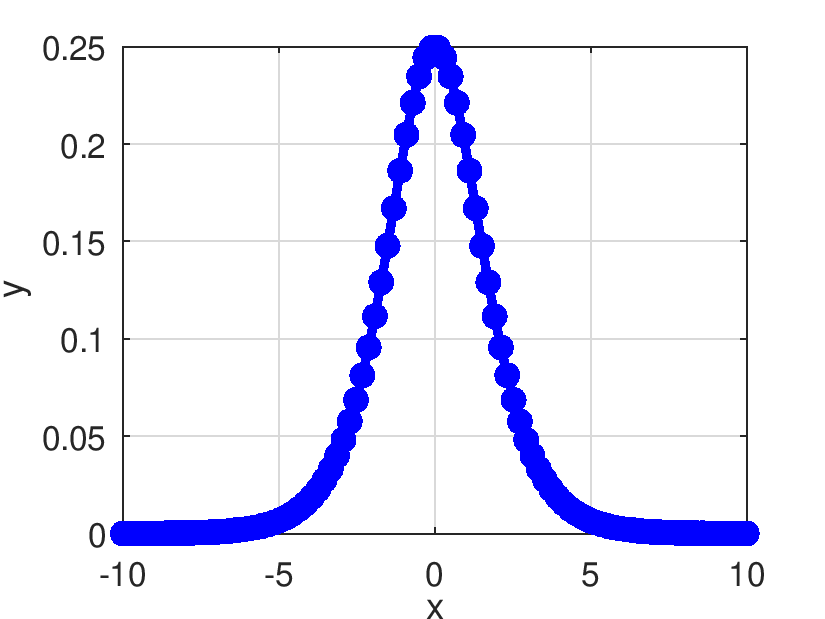
![\[ \frac{\partial Pds::Sigmoid(x)}{\partial x}=\frac{e^{-x}}{(1+e^{-x})^2} \]](form_441.png)
| [in] | X | La variable a evaluar |
| double Pds::DSigmoid | ( | double | x | ) |
Retorna el resultado de evaluar elemento a elemento la derivada de la función sigmoid.

![\[ \frac{\partial Pds::Sigmoid(x)}{\partial x}=\frac{e^{-x}}{(1+e^{-x})^2} \]](form_441.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::SoftMax | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar la función SoftMax.
![]()
![\[ y_i=\frac{e^{x_i}}{\sum_{j}e^{x_j}} \]](form_443.png)
| [in] | X | El vector de entrada. |
| Pds::Matrix Pds::HardMax | ( | const Pds::Matrix & | X | ) |
Retorna el resultado de evaluar la función HardMax (ArgMax in Machine learning).
![]()
![\[
y_i=
\left\{
\begin{matrix}
1 & if(x_i==max_x)\\
0 & else
\end{matrix}
\right.
\]](form_445.png)
| [in] | X | El vector de entrada. |
| unsigned int Pds::Factorial | ( | unsigned int | n | ) |
Evalúa factorial de n, igual a n!.
![]()
Tiene problemas de presición, cuando n es muy grande.
| [in] | n | Valor de entrada. |
| unsigned int Pds::NchooseK | ( | unsigned int | n, |
| unsigned int | k | ||
| ) |
Retorna el combinatorio (n,k)
![\[ {n \choose k}=\frac{n!}{k!(n-k)!} \]](form_447.png)
| [in] | n | Valor superior del combinatorio. |
| [in] | k | Valor inferior del combinatorio. |
| unsigned int Pds::NmultichooseK | ( | unsigned int | n, |
| unsigned int | k | ||
| ) |
Retorna el combinatorio (n,k)
![\[ \left({n \choose k}\right)={{n+k-1} \choose k} \]](form_448.png)
| [in] | n | Valor superior del combinatorio. |
| [in] | k | Valor inferior del combinatorio. |
| double Pds::UnitStep | ( | double | x | ) |
Retorna el resultado de evaluar la función UnitStep().
![]()
![]()
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::UnitStep | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar la función UnitStep().
![]()
![]()
![]()
| [in] | A | La matriz a evaluar |
| double Pds::UnitRamp | ( | double | x | ) |
Retorna el resultado de evaluar la función UnitRamp().
![]()
![]()
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::UnitRamp | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar la función UnitRamp().
![]()
![]()
![]()
| [in] | A | La matriz a evaluar |
| double Pds::SignNZ | ( | double | x | ) |
Retorna el resultado de evaluar la función Sign Non Zero.
![]()
![]()
| [in] | x | La variable a evaluar |
| double Pds::Sign | ( | double | x | ) |
Retorna el resultado de evaluar la función Sign.
![]()
![]()
![]()
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::Sign | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función Sign.
![]()
![]()
![]()
![]()
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::Round | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función round.
![]()
| [in] | A | La matriz a evaluar |
| double Pds::MuLaw | ( | double | x, |
| double | Mu | ||
| ) |
Retorna el resultado de evaluar la ![]() (ley mu).
(ley mu).
![\[ y=F(x)=sgn(x){\frac {\ln(1+\mu |x|)}{\ln(1+\mu )}}~~~~-1\leq x\leq 1 \]](form_464.png)
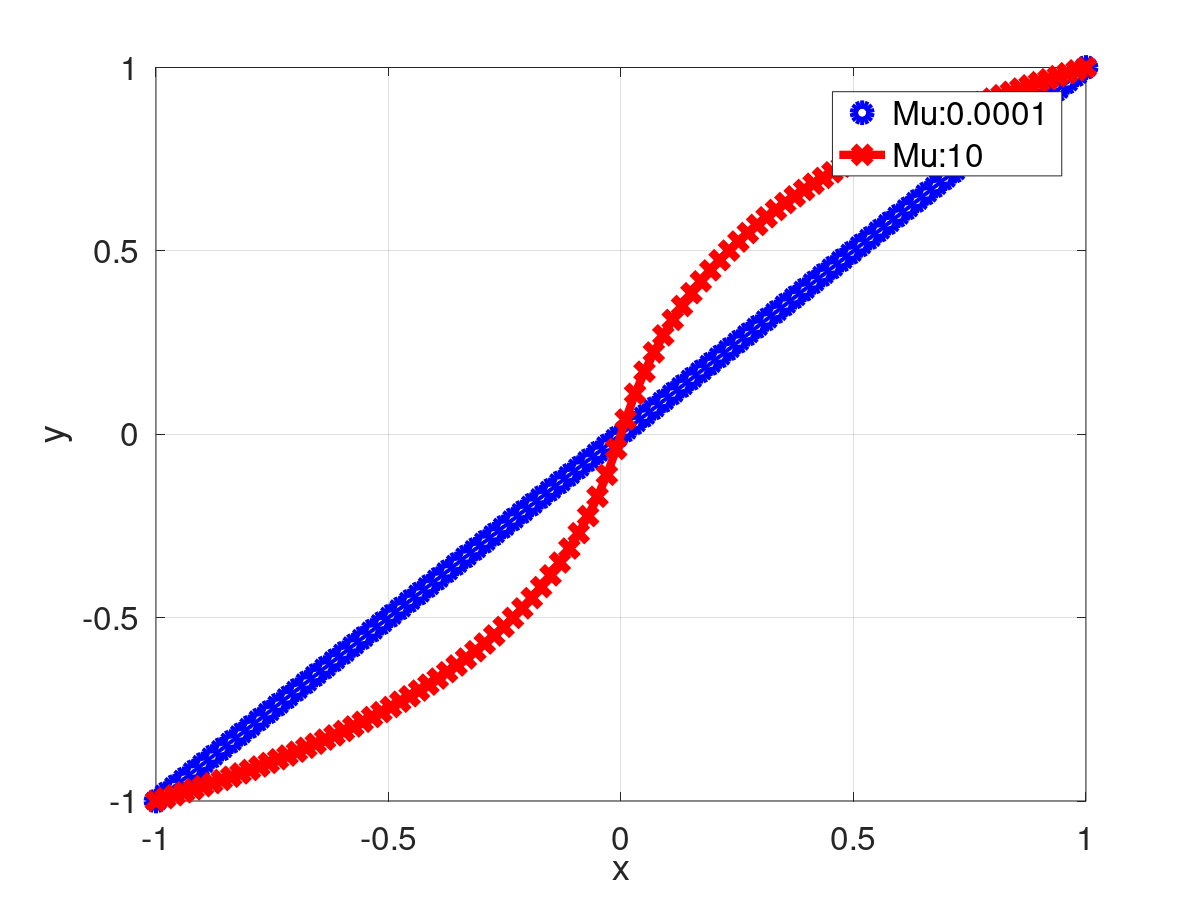
| [in] | x | La matriz a evaluar |
| [in] | Mu | El factor mu. |
| Pds::Matrix Pds::MuLaw | ( | const Pds::Matrix & | A, |
| double | Mu | ||
| ) |
Retorna el resultado de evaluar la ![]() . (ley mu).
. (ley mu).
![\[ y=F(x)=sgn(x){\frac {\ln(1+\mu |x|)}{\ln(1+\mu )}}~~~~-1\leq x\leq 1 \]](form_464.png)

| [in] | A | La matriz a evaluar |
| [in] | Mu | El factor mu. |
| double Pds::MuLawInv | ( | double | y, |
| double | Mu | ||
| ) |
Retorna el resultado de evaluar la ![]() (ley mu).
(ley mu).
![\[ F^{-1}(y)={sgn}(y){1 \over \mu }{\Bigl (}(1+\mu )^{|y|}-1{\Bigr )}~~~~-1\leq y\leq 1 \]](form_465.png)
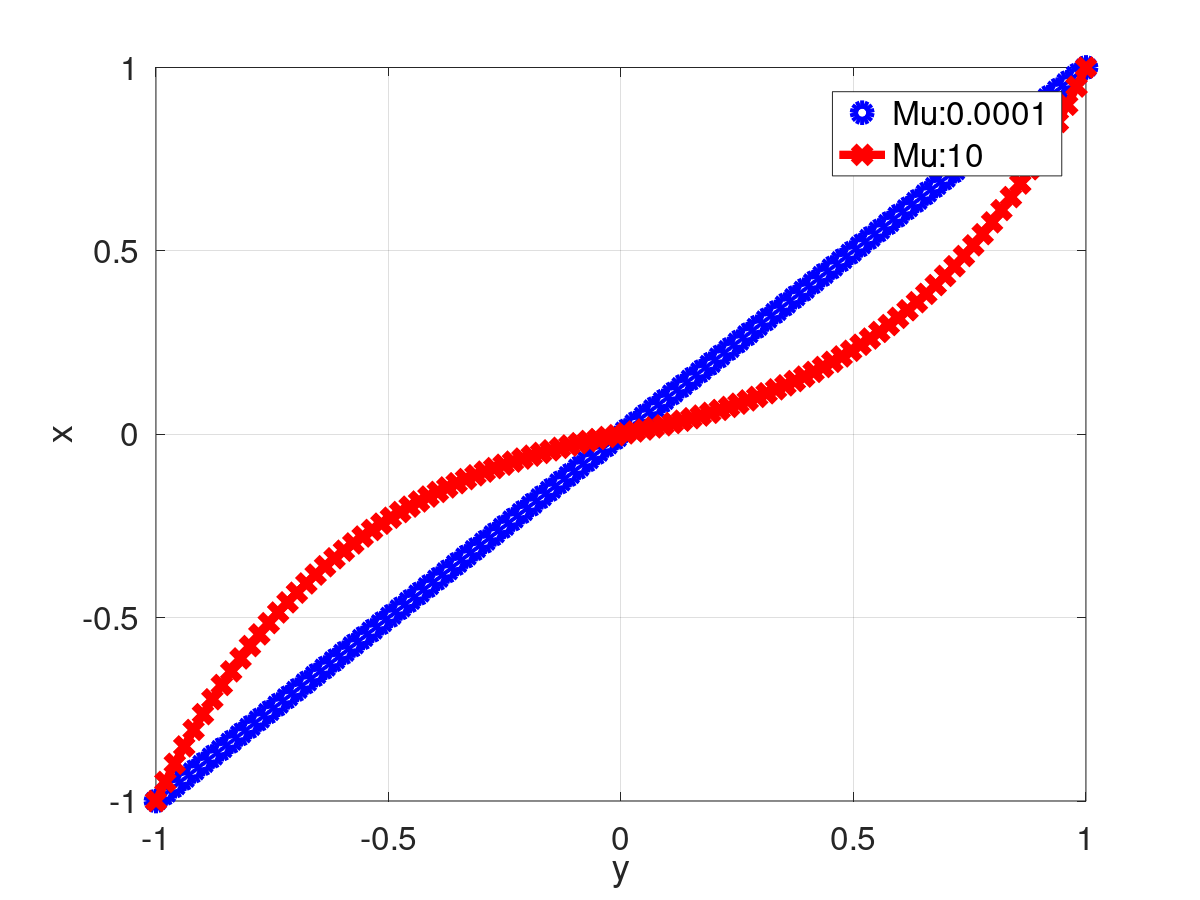
| [in] | y | La matriz a evaluar |
| [in] | Mu | El factor mu. |
| Pds::Matrix Pds::MuLawInv | ( | const Pds::Matrix & | A, |
| double | Mu | ||
| ) |
Retorna el resultado de evaluar la ![]() . (ley mu).
. (ley mu).
![\[ F^{-1}(y)={sgn}(y){1 \over \mu }{\Bigl (}(1+\mu )^{|y|}-1{\Bigr )}~~~~-1\leq y\leq 1 \]](form_465.png)

| [in] | A | La matriz a evaluar |
| [in] | Mu | El factor mu. |
| Pds::Matrix Pds::Conv2DCh | ( | const std::vector< Pds::Matrix > & | A, |
| const std::vector< Pds::Matrix > & | Kernel, | ||
| const std::vector< unsigned int > & | Strides = {1, 1}, |
||
| Pds::Ra::Padding | Padding = Pds::Ra::Valid |
||
| ) |
Calcula la convolución de todos los canales entre A y Kernel.
![\[
\mathbf{D}=\sum \limits_{n}^{N} \mathbf{A}[n].Conv2D(\mathbf{Kernel}[n])
\]](form_466.png)
| [in] | A | Vector de matrices a aplicar la convolución. Debe tener el mismo número de canales que Kernel. Todos los canales deben tener el mismo tamaño. |
| [in] | Kernel | Vector de matrices a aplicar la convolución. Debe tener el mismo número de canales que A. Todos los canales deben tener el mismo tamaño. |
| [in] | Strides | Paso del convolucionador. |
| [in] | Padding | indica el tipo de pading de la convolución lo cual afecta al tamaño de la matriz de salida. |
| Pds::Vector Pds::Conv1DCh | ( | const std::vector< Pds::Vector > & | A, |
| const std::vector< Pds::Vector > & | Kernel, | ||
| unsigned int | Strides = 1, |
||
| Pds::Ra::Padding | Padding = Pds::Ra::Valid |
||
| ) |
Calcula la convolución de todos los canales entre A y Kernel.
![\[
\mathbf{D}=\sum \limits_{n}^{N} \mathbf{A}[n].Conv1D(\mathbf{Kernel}[n])
\]](form_467.png)
| [in] | A | Vector de vectores a aplicar la convolución. Debe tener el mismo número de canales que Kernel. Todos los canales deben tener el mismo tamaño. |
| [in] | Kernel | Vector de vectores a aplicar la convolución. Debe tener el mismo número de canales que A. Todos los canales deben tener el mismo tamaño. |
| [in] | Strides | Paso del convolucionador. |
| [in] | Padding | indica el tipo de pading de la convolución lo cual afecta al tamaño de la matriz de salida. |
| Pds::Matrix Pds::Conv1DCh | ( | const std::vector< Pds::Matrix > & | A, |
| const std::vector< Pds::Vector > & | Kernel, | ||
| unsigned int | Strides = 1, |
||
| Pds::Ra::Padding | Padding = Pds::Ra::Valid |
||
| ) |
Calcula la convolución de todos los canales entre A y Kernel.
![\[
\mathbf{D}=\sum \limits_{n}^{N} \mathbf{A}[n].Conv1D(\mathbf{Kernel}[n])
\]](form_467.png)
| [in] | A | Vector de vectores a aplicar la convolución. Debe tener el mismo número de canales que Kernel. Todos los canales deben tener el mismo tamaño. |
| [in] | Kernel | Vector de vectores a aplicar la convolución. Debe tener el mismo número de canales que A. Todos los canales deben tener el mismo tamaño. |
| [in] | Strides | Paso del convolucionador. |
| [in] | Padding | indica el tipo de pading de la convolución lo cual afecta al tamaño de la matriz de salida. |
| Pds::Matrix Pds::Abs | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función valor absoluto.
![]()
| [in] | A | La matriz a evaluar |
| double Pds::Logit | ( | double | x | ) |
Retorna el resultado de evaluar la función logit.
![\[ log\left(\frac{x}{1-x}\right)\equiv Pds::Sigmoid^{-1}(x)\]](form_469.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::Logit | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función logit.
![\[ log\left(\frac{A}{1-A}\right) \equiv Pds::Sigmoid^{-1}(A) \]](form_470.png)
| [in] | A | La matriz a evaluar |
| Pds::Matrix Pds::Erf | ( | const Pds::Matrix & | A | ) |
Calcula el valor de la función ![]() .
.
![\[ erf (x)=\frac {2}{\sqrt{\pi}} \int _{0}^{x}e^{-t^{2}}\,dt \]](form_472.png)
![]()
| [in] | A | Matriz a procesar. |
| double Pds::Sinc | ( | double | x | ) |
Retorna el resultado de evaluar la función sinc.
![\[ sinc(x)=\frac{sin(x)}{x} \]](form_474.png)
| [in] | x | La variable a evaluar |
| Pds::Matrix Pds::Sinc | ( | const Pds::Matrix & | A | ) |
Retorna el resultado de evaluar elemento a elemento la función sinc.
![\[ sinc(x)=\frac{sin(x)}{x} \]](form_474.png)
![]()
| [in] | A | La matriz a evaluar |
 1.9.4
1.9.4