Clase que implementa una matriz de valores reales. Más...

Namespaces
namespace	Pds
	Nombre de espacio para Pds (Procesamiento Digital de Senales)

Estructuras de datos
class	Pds::Matrix
	La clase tipo Pds::Matrix . Esta clase genera una matriz de Nlin lineas y Ncol columnas. Para usar incluir Pds/Matrix. Más...

typedefs
typedef std::vector< Pds::Matrix >	Pds::SampleBlock
	Definición de un tipo de dato Pds::SampleBlock. Más...

typedef std::vector< std::vector< Pds::Matrix > >	Pds::BatchBlock
	Definición de un tipo de dato Pds::BatchBlock. Más...

Constructores
Crean una objeto Pds::Matrix
	Pds::Matrix::Matrix (void)
	Crea un objeto de tipo Pds::Matrix vacio. Más...

	Pds::Matrix::Matrix (unsigned int N)
	Crea un objeto de tipo Pds::Matrix de N lineas y N columnas, con elementos inicializados con cero. Más...

	Pds::Matrix::Matrix (const Pds::Size &S)
	Crea un objeto de tipo Pds::Matrix con elementos inicializados con cero. Más...

	Pds::Matrix::Matrix (const Pds::Size &S, double val)
	Crea un objeto de tipo Pds::Matrix con elementos inicializados con val. Más...

	Pds::Matrix::Matrix (const Pds::Matrix &B)
	Crea un objeto de tipo Pds::Matrix copiando datos desde otra matriz. Este es un Copy assignment constructor. Más...

template<class Datum >
	Pds::Matrix::Matrix (const Pds::Array< Datum > &B)
	Crea un objeto de tipo Pds::Matrix copiando datos desde un arreglo. Más...

	Pds::Matrix::Matrix (const char *str)
	Crea un objeto de tipo Pds::Matrix copiando datos desde una cadena. Más...

	Pds::Matrix::Matrix (const std::string &str)
	Crea un objeto de tipo Pds::Matrix copiando datos desde una std::string. Más...

	Pds::Matrix::Matrix (unsigned int Nlin, unsigned int Ncol)
	Crea un objeto de tipo Pds::Matrix con elementos inicializados con cero. Más...

	Pds::Matrix::Matrix (unsigned int Nlin, unsigned int Ncol, double val)
	Crea un objeto de tipo Pds::Matrix con elementos inicializados con val. Más...

	Pds::Matrix::Matrix (double(*func)(double), const Pds::Matrix &B)
	Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz. Más...

	Pds::Matrix::Matrix (double(*func)(double, double), const Pds::Matrix &B, double var)
	Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz. Más...

	Pds::Matrix::Matrix (double(*func)(double, double), const Pds::Matrix &B, const Pds::Matrix &C)
	Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz. Más...

	Pds::Matrix::Matrix (double(*func)(double, double, double), const Pds::Matrix &B, const Pds::Matrix &C, double var)
	Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz. Más...

	Pds::Matrix::Matrix (double(*func)(double, double, double), const Pds::Matrix &X, const Pds::Matrix &Y, const Pds::Matrix &Z)
	Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz. Más...

	Pds::Matrix::Matrix (double(*func)(double, double, double, double), const Pds::Matrix &X, const Pds::Matrix &Y, const Pds::Matrix &Z, double var)
	Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz. Más...

	Pds::Matrix::Matrix (double(*func)(double, double, double, double), const Pds::Matrix &X, const Pds::Matrix &Y, const Pds::Matrix &Z, const Pds::Matrix &W)
	Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz. Más...

	Pds::Matrix::Matrix (Pds::Ra::FormatType Type, std::string filepath)
	Crea un objeto de tipo Pds::Matrix copiando datos desde un archivo. Más...

	Pds::Matrix::Matrix (const std::vector< Pds::Point2D > &P)
	Crea una matriz de dos columnas, en la primera columna estan los elementos X y en la segunda columna los elelentos Y. Más...

	Pds::Matrix::Matrix (const std::vector< Pds::Position > &P)
	Crea una matriz de dos columnas, en la primera columna estan los elementos Lin y en la segunda columna los elelentos Col. Más...

template<class Datum >
	Pds::Matrix::Matrix (const std::vector< Datum > &P)
	Crea una matriz de una columna, en esa columna estan los elementos del vector. Más...

template<class Datum >
	Pds::Matrix::Matrix (unsigned int Nlin, unsigned int Ncol, const std::vector< Datum > &P)
	Crea una matriz Nlin lineas y Ncol columnas usando los elementos del vector. Más...

template<class Datum >
	Pds::Matrix::Matrix (const std::initializer_list< Datum > &list)
	Crea una matriz de una columna, en esa columna estan los elementos del vector. Más...

	Pds::Matrix::~Matrix ()

Métodos de estado
Indican o establecen el estado de una matriz.
bool	Pds::Matrix::IsEmpty (void) const
	Verifica si la matriz es nula es decir con lineas o columnas cero o arreglo NULL. Más...

bool	Pds::Matrix::IsNotEmpty (void) const
	Verifica si la matriz NO es nula, es decir con lineas y columnas diferentes cero y arreglo diferente de NULL. Más...

bool	Pds::Matrix::IsSimilarTo (const Pds::Matrix &B) const
	Verifica si las matrices son similares en tamaño. Más...

bool	Pds::Matrix::IsNotSimilarTo (const Pds::Matrix &B) const
	Verifica si las matrices son similares en tamaño. Más...

bool	Pds::Matrix::IsMulBy (const Pds::Matrix &B) const
	Verifica si las matrices son multiplicables. Más...

bool	Pds::Matrix::IsNotMulBy (const Pds::Matrix &B) const
	Verifica si las matrices son multiplicables. Más...

bool	Pds::Matrix::IsInRange (unsigned int lin, unsigned int col) const
	Verifica si la posición pertenece a la matriz. Más...

bool	Pds::Matrix::IsNotInRange (unsigned int lin, unsigned int col) const
	Verifica si la posición NO pertenece a la matriz. Más...

bool	Pds::Matrix::IsInSizeRange (double lin, double col) const
	Verifica si la posición (lin,col) pertenece al rango de la matriz. Más...

bool	Pds::Matrix::IsRowMatrix (void) const
	Verifica si la matriz tiene solo una linea. Más...

bool	Pds::Matrix::IsColMatrix (void) const
	Verifica si la matriz tiene solo una columna. Más...

bool	Pds::Matrix::IsZero (void) const
	Verifica si la matriz está llena de zeros. Más...

bool	Pds::Matrix::IsLeq (double val) const
	Verifica si cada elemento de la matriz es menor a el valor val. Más...

bool	Pds::Matrix::IsLeq (const Pds::Matrix &B) const
	Verifica si cada elemento de la matriz es menor igual a cada elemento de la matriz B. Más...

bool	Pds::Matrix::IsGeq (double val) const
	Verifica si cada elemento de la matriz es mayor a el valor val. Más...

bool	Pds::Matrix::IsGeq (const Pds::Matrix &B) const
	Verifica si cada elemento de la matriz es mayor igual a cada elemento de la matriz B. Más...

bool	Pds::Matrix::IsEqualTo (double val) const
	Verifica si cada elemento de la matriz es igual a el valor val. Más...

bool	Pds::Matrix::IsEqualTo (const Pds::Matrix &B) const
	Verifica si cada elemento de la matriz es igual a cada elemento de la matriz B. Más...

bool	Pds::Matrix::HasLeq (double val) const
	Verifica si existe al menos un elemento de la matriz menor o igual a el valor val. Más...

bool	Pds::Matrix::HasGeq (double val) const
	Verifica si existe al menos un elemento de la matriz mayor o igual a el valor val. Más...

bool	Pds::Matrix::HasInf (void) const
	Verifica si la matriz tiene algun valor infinito. Más...

bool	Pds::Matrix::HasNan (void) const
	Verifica si la matriz tiene algun valor NAN (Not A Number). Más...

bool	Pds::Matrix::HasNotFinite (void) const
	Verifica si la matriz tiene elementos no finitos (+inf, -inf y NAN). Más...

Métodos de inicialización
Establecen los valores de las matrices.
bool	Pds::Matrix::FillRandC (double p1)
	Inicializa la matriz con números aleatórios unos y ceros, la probabilidad de 1 es p1. Más...

bool	Pds::Matrix::FillRandN (void)
	Inicializa la matriz con números aleatórios, distribuidos usando una distribución Gaussiana normalizada con media 0 y desvío padrón 1.0. Más...

bool	Pds::Matrix::FillRandN (double U, double Sigma)
	Inicializa la matriz con números aleatórios, distribuidos usando una distribución Gaussiana con media U y desvío padrón Sigma. Más...

bool	Pds::Matrix::FillRandU (void)
	Inicializa la matriz con números aleatórios, distribuidos uniformemente, desde 0 a 1.0, incluyendo 0 y excluyendo 1.0. Más...

bool	Pds::Matrix::FillRandU (int a, int b)
	Inicializa la matriz con números aleatórios, distribuidos uniformemente, desde a a b, incluyendo a y b. Más...

bool	Pds::Matrix::FillRandU (double a, double b)
	Inicializa la matriz con números aleatórios, distribuidos uniformemente, desde a a b, incluyendo a y b. Más...

bool	Pds::Matrix::FillId (void)
	Inicializa la matriz con el valor de la posición de cada elemento. Más...

bool	Pds::Matrix::FillBcd (unsigned int n)
	Escribe un número en digital codificado en binário (BCD), escribe primero en una columna entera y luego pasa a la siguiente. Más...

bool	Pds::Matrix::Fill (Pds::AbstractRV &RV)
	Inicializa la matriz con un valor aleatório. Más...

bool	Pds::Matrix::Fill (double val)
	Inicializa la matriz con un valor constante. Más...

template<class Datum >
bool	Pds::Matrix::Fill (const std::vector< Datum > &P)
	Inicializa la matriz con un valor constante. Más...

bool	Pds::Matrix::FillLinSpace (double a, double b)
	Inicializa la matriz con un espacio linear entre begin y end. Se inicializa primero una columna ante de pasar ala siguiente. Más...

Métodos de tamaño
Herramientas genéricas para lectura y escritura de datos.
unsigned int	Pds::Matrix::Nlin (void) const
	Retorna el número de lineas de la matriz. Más...

unsigned int	Pds::Matrix::Ncol (void) const
	Retorna el número de columnas de la matriz. Más...

unsigned int	Pds::Matrix::Nel (void) const
	Retorna el número de elementos de la matriz (Nlin x Ncol). Más...

Pds::Size	Pds::Matrix::Size (void) const
	Retorna un objeto de tipo Pds::Size con el número de lineas y columans. Más...

unsigned int	Pds::Matrix::LinEnd (void) const
	Retorna el identificador de la ultima linea de la matriz. Más...

unsigned int	Pds::Matrix::ColEnd (void) const
	Retorna el identificador de la ultima columna de la matriz. Más...

unsigned int	Pds::Matrix::End (void) const
	Retorna el identificador del ultimo elemento de la matriz. Más...

Métodos get y set de elementos
Herramientas genéricas para lectura y escritura de datos.
double	Pds::Matrix::Get (unsigned int id) const
	Retorna el valor en la posición del índice id, hace una verificación si la posición existe. Más...

double	Pds::Matrix::Get (unsigned int lin, unsigned int col) const
	Retorna el valor en la posición (lin,col), hace una verificación si la posición existe. Más...

Pds::Vector	Pds::Matrix::Get (const std::vector< Pds::Position > &P) const
	Retorna el valor en las posiciones P[n]. Hace una verificación si la posiciones existen. Más...

double	Pds::Matrix::Get (const Pds::Position &P) const
	Retorna el valor en la posición (lin,col), hace una verificación si la posición existe. Más...

const double &	Pds::Matrix::GetRaw (unsigned int lin, unsigned int col) const
	Retorna una variable double en la posición (lin,col) de la array. Más...

void	Pds::Matrix::SetRaw (unsigned int lin, unsigned int col, const double &val)
	Establece una variable double en la posición (lin,col) de la array. Más...

bool	Pds::Matrix::Set (unsigned int id, double val)
	Escribe el valor en la posición del índice id, hace una verificación si la posición existe. Más...

bool	Pds::Matrix::Set (unsigned int lin, unsigned int col, double val)
	Escribe el valor en la posición (lin,col), hace una verificación si la posición existe. Más...

double &	Pds::Matrix::In (unsigned int lin, unsigned int col)
	Retorna una variable double en la posición (lin,col) de la matriz. Hace una verificación para evitar leer o escribir fuera de la memoria, con este fin hace lin=linNlin y col=colNcol. Más...

double &	Pds::Matrix::In (unsigned int id)
	Retorna una variable double en la posición (id) de la matriz. Hace una verificación para evitar leer o escribir fuera de la memoria, con este fin hace id=id%(Nlin*Ncol). Más...

double	Pds::Matrix::Bilinear (double lin, double col) const
	Retorna el valor en la posición (lin,col), usando una interpolación bilinear, valores fuera del rango de la matriz retornan cero. Más...

Métodos get y set de matrices y vectores
Herramientas genericas para lectura y escritura de datos.
Pds::Vector	Pds::Matrix::GetDiagonal (void) const
	Retorna un vector columna copia de los valores de la diagonal de la matriz. Más...

bool	Pds::Matrix::SetDiagonal (const Pds::Vector V)
	Copia un vector columna en una diagonal de la matriz. Si los tamaños son diferentes, se interceptan las matrices y se copia solamente en la intersección. Más...

bool	Pds::Matrix::SetDiagonal (double val)
	Copia un valor en una diagonal de la matriz. Copia hasta donde exista la diagonal. Más...

Pds::Matrix	Pds::Matrix::GetMatrix (unsigned int lin_init, unsigned int col_init, unsigned int lin_end, unsigned int col_end) const
	Retorna una sub matriz desde la posición (lin_init,col_init) hasta (lin_end,col_end), inclusive. Hace una verificación si la posición existe, si no existe llena con ceros. Más...

Pds::Matrix	Pds::Matrix::GetMatrix (unsigned int lin_init, unsigned int col_init, Pds::Size size) const
	Retorna una sub matriz desde la posición (lin_init,col_init) hasta (lin_end,col_end), inclusive. Hace una verificación si la posición existe, si no existe llena con ceros. Más...

bool	Pds::Matrix::SetMatrix (unsigned int lin, unsigned int col, const Pds::Matrix &B)
	Copia en si mismo (A) en la posicion (lin,col), el contenido de una matriz B. Si a matriz B no cabe em A se retorna false. Más...

Pds::Matrix	Pds::Matrix::GetRow (unsigned int lin) const
	Retorna una matriz linea escojida en la linea lin. Hace una verificación si la linea existe, si no existe devuelve una matriz vacia. Más...

bool	Pds::Matrix::GetRow (unsigned int lin, Pds::Matrix &Row) const
	Retorna una matriz linea escojida en la linea lin de X. Hace una verificación si la linea existe y si Row es linea, si no existe devuelve false. Más...

Pds::Vector	Pds::Matrix::GetRowAsColVector (unsigned int lin) const
	Retorna un vector columna copia de una linea de la matriz. Más...

bool	Pds::Matrix::GetRowAsColVector (unsigned int lin, Pds::Vector &V) const
	Retorna un vector columna copia de una linea de la matriz. Más...

bool	Pds::Matrix::GetRows (unsigned int lin_init, unsigned int lin_end, Pds::Matrix &B) const
	Retorna una sub matriz escojida desde la linea lin_init hasta lin_end, inclusive. Hace una verificación si la linea existe, si no existe llena esta con ceros. Más...

Pds::Matrix	Pds::Matrix::GetRows (unsigned int lin_init, unsigned int lin_end) const
	Retorna una sub matriz escojida desde la linea lin_init hasta lin_end, inclusive. Hace una verificación si la linea existe, si no existe llena esta con ceros. Más...

Pds::Matrix	Pds::Matrix::GetRows (std::list< unsigned int > List) const
	Retorna una sub matriz escojida desde una lista de indices de lineas. Hace una verificación si los indices existen, si alguno no existe devuelve una matriz vacia. Más...

Pds::Matrix	Pds::Matrix::GetRows (std::vector< unsigned int > Vec) const
	Retorna una sub matriz escojida desde una lista de indices de lineas. Hace una verificación si los indices existen, si alguno no existe devuelve una matriz vacia. Más...

Pds::Matrix	Pds::Matrix::GetRowsRand (unsigned int N) const
	Retorna una sub matriz escojiendo N lineas aleatoriamente (sin repetición). Más...

Pds::Matrix	Pds::Matrix::GetCol (unsigned int col) const
	Retorna una matriz columna escojida en la columna col. Hace una verificación si la columna existe, si no existe devuelve una matriz vacia. Más...

bool	Pds::Matrix::GetCol (unsigned int col, Pds::Matrix &MatCol) const
	Retorna una matriz columna escojida en la columna col. Hace una verificación si la columna existe y tiene el tamanho de MatCol, si no existe devuelve false. Más...

Pds::Vector	Pds::Matrix::GetColVector (unsigned int col) const
	Retorna un vector columna copia de una columna de la matriz. Más...

bool	Pds::Matrix::GetColVector (unsigned int col, Pds::Vector &U) const
	Copia a un vector columna el contenido de una columna de la matriz. Más...

Pds::Matrix	Pds::Matrix::GetCols (unsigned int col_init, unsigned int col_end) const
	Retorna una sub matriz escojida desde la columna col_init hasta col_end, inclusive. Hace una verificación si la columna existe, si no existe llena esta con ceros. Más...

Pds::Matrix	Pds::Matrix::GetCols (std::list< unsigned int > List) const
	Retorna una sub matriz escojida desde una lista de indices de columnas. Hace una verificación si los indices existen, si alguno no existe devuelve una matriz vacia. Más...

Pds::Matrix	Pds::Matrix::GetCols (const std::initializer_list< unsigned int > List) const
	Retorna una sub matriz escojida desde una lista de indices de columnas. Hace una verificación si los indices existen, si alguno no existe devuelve una matriz vacia. Más...

Pds::Matrix	Pds::Matrix::GetCols (std::vector< unsigned int > Vec) const
	Retorna una sub matriz escojida desde una lista de indices de columnas. Hace una verificación si los indices existen, si alguno no existe devuelve una matriz vacia. Más...

Pds::Matrix	Pds::Matrix::GetColsRand (unsigned int N) const
	Retorna una sub matriz escojiendo N columnas aleatoriamente (sin repetición). Más...

bool	Pds::Matrix::SetRowValue (unsigned int lin, double value)
	Copia un valor en una linea de la matriz. Más...

bool	Pds::Matrix::SetRowVector (unsigned int lin, const Pds::Vector &X)
	Copia un vector en una linea de la matriz. Más...

bool	Pds::Matrix::SetColValue (unsigned int col, double value)
	Copia un valor en una columna de la matriz. Más...

bool	Pds::Matrix::SetColVector (unsigned int col, const Pds::Vector &V)
	Copia un vector columna en una columna de la matriz. Si los tamaños son diferentes, se interceptan las matrices y se copia solamente en la intersección. Más...

bool	Pds::Matrix::SetColVector (unsigned int col, double(*func)(double), const Pds::Vector &V)
	Copia un vector columna en una columna de la matriz, despues de evaluar el vector en una funcion. Si los tamaños son diferentes, se interceptan las matrices y se copia solamente en la intersección. Más...

bool	Pds::Matrix::SetColVector (unsigned int col, double(*func)(double, double), const Pds::Vector &V, double var)
	Copia un vector columna en una columna de la matriz, despues de evaluar el vector en una funcion. Si los tamaños son diferentes, se interceptan las matrices y se copia solamente en la intersección. Más...

std::vector< Pds::Point2D >	Pds::Matrix::GetPoint2DsFromCols (unsigned int colx, unsigned int coly) const
	Copia un par de columnas de la matriz para convertirlas en un vector de Pds::Point2D. Más...

std::vector< double >	Pds::Matrix::ToStdVector (void) const
	Retorna un std::vector con los elelentos de la matriz, lee columna a columna. Más...

Métodos de opreaciones sobre las lineas de la matriz
operaciones con lineas
bool	Pds::Matrix::RowAddAssig (unsigned int lin1, unsigned int lin2, double alpha)
	Multiplica los valores de la linea lin2 por alfa y el resultado es sumado a los valores de la linea lin1. Más...

bool	Pds::Matrix::RowMulAssig (unsigned int lin, double alpha)
	Multiplica la linea lin por alpha. Más...

bool	Pds::Matrix::RowDivAssig (unsigned int lin, double alpha)
	Divide la linea lin por alpha. Más...

bool	Pds::Matrix::RowSwap (unsigned int lin1, unsigned int lin2)
	Intercambia los valores de las lineas de una matriz. Más...

int	Pds::Matrix::RowSwapBelow (unsigned int n)
	Si el n-avo elemento de la diagonal es cero entonces intercambia la linea n de la matriz con cualquier linea inferior con elemento diferente de cero en la columna n. Más...

bool	Pds::Matrix::RowReduction (void)
	Convierte la matriz en una matriz reducida. Más...

bool	Pds::Matrix::RowDivByAbsMax (void)
	Normaliza cada linea de la matriz dividiendola por el máximo valor absoluto de la linea. Si la linea tiene solo ceros esta no es modificada. Más...

Métodos estadísticos
Herramientas genéricas
std::map< int, unsigned int >	Pds::Matrix::IntegerCount (void) const
	Cuenta la cantidad de elementos enteros. Más...

std::set< int >	Pds::Matrix::IntegerSet (void) const
	Set de elementos enteros. Más...

double	Pds::Matrix::MultiplyValues (void) const
	Calcula el valor de la multiplicación de elementos en la matriz. Más...

double	Pds::Matrix::Sum (void) const
	Calcula el valor de la suma de elementos de la matriz. Más...

double	Pds::Matrix::Mean (void) const
	Calcula el valor medio de la matriz. Más...

Pds::Matrix	Pds::Matrix::MeanInCols (void) const
	Calcula el valor medio de las columnas de la matriz. Más...

Pds::Vector	Pds::Matrix::MeanInRows (void) const
	Calcula la media de cada linea de la matriz. Más...

double	Pds::Matrix::Std (double *mean=NULL) const
	Calcula el valor del desvío padrón de la matriz. Más...

Pds::Vector	Pds::Matrix::StdInRows (void) const
	Calcula el standard deviation de cada linea de la matriz. Más...

Pds::Matrix	Pds::Matrix::StdInCols (void) const
	Calcula el standard deviation de cada columna de la matriz. Más...

bool	Pds::Matrix::MeanStdInRows (Pds::Vector &Mean, Pds::Vector &Std) const
	Calcula la media y el standard deviation de cada linea de la matriz. Más...

bool	Pds::Matrix::MeanStdInCols (Pds::Matrix &Mean, Pds::Matrix &Std) const
	Calcula la media y el standard deviation de cada linea de la matriz. Más...

double	Pds::Matrix::Var (double *mean=NULL) const
	Calcula el valor de la varianza de la matriz. Más...

double	Pds::Matrix::Max (unsigned int *id=NULL) const
	Calcula el máximo valor de la matriz. Más...

double	Pds::Matrix::Min (unsigned int *id=NULL) const
	Calcula el mínimo valor de la matriz. Más...

double	Pds::Matrix::MaxAbs (unsigned int *id=NULL) const
	Calcula el máximo valor del valor absoluto de la matriz. Más...

double	Pds::Matrix::MinAbs (unsigned int *id=NULL) const
	Calcula el mínimo valor del valor absoluto de la matriz. Más...

Pds::Matrix	Pds::Matrix::MaxInCols (void) const
	Calcula el máximo en cada columna de la matriz. Más...

Pds::Matrix	Pds::Matrix::MinInCols (void) const
	Calcula el mínimo en cada columna de la matriz. Más...

Pds::Matrix	Pds::Matrix::MaxInCols (std::vector< unsigned int > &Lin) const
	Calcula el máximo en cada columna de la matriz. Más...

Pds::Matrix	Pds::Matrix::MinInCols (std::vector< unsigned int > &Lin) const
	Calcula el mínimo en cada columna de la matriz. Más...

Pds::Matrix	Pds::Matrix::MaxInCols (Pds::Array< unsigned int > &Lin) const
	Calcula el máximo en cada columna de la matriz. Más...

Pds::Matrix	Pds::Matrix::MinInCols (Pds::Array< unsigned int > &Lin) const
	Calcula el mínimo en cada columna de la matriz. Más...

Pds::Matrix	Pds::Matrix::MaxAbsInCols (void) const
	Retorna una matriz con el máximo valor absoluto de cada columna. Más...

Pds::Vector	Pds::Matrix::MaxAbsInRows (void) const
	Retorna un vector con el máximo valor absoluto de cada linea. Más...

Pds::Vector	Pds::Matrix::MinAbsInRows (void) const
	Retorna un vector con el mínimo valor absoluto de cada linea. Más...

Pds::Vector	Pds::Matrix::MaxInRows (void) const
	Retorna un vector con el máximo valor de cada linea. Más...

Pds::Vector	Pds::Matrix::MinInRows (void) const
	Retorna un vector con el mínimo valor de cada linea. Más...

Pds::Vector	Pds::Matrix::ArgMaxInRows (void) const
	Retorna un vector con el ID del máximo valor de cada linea. Más...

Pds::Vector	Pds::Matrix::ArgMinInRows (void) const
	Retorna un vector con el ID del mínimo valor de cada linea. Más...

bool	Pds::Matrix::ScalingColsAnalysis (Pds::Vector &Mean, Pds::Vector &Std)
	Calcula la media y el standard deviation de cada columna de la matriz. Si el std de la columna es cero esta no es normalizada. Más...

bool	Pds::Matrix::ScalingColsWith (const Pds::Vector &Mean, const Pds::Vector &Std)
	Escala cada columna de la matriz usando la media y el standard deviation de cada columna de la matriz. Si el std de la columna es cero esta no es normalizada. Más...

long int	Pds::Matrix::CountRoundEqualIn (const Pds::Matrix &B) const
	Calcula el número de elementos enteros iguales entre las matrices A y B. Más...

double	Pds::Matrix::Accuracy (const Pds::Matrix &B, double Umbral) const
	Calcula el valor de la Accuracy entre los elementos de las matrices A (Self) y B. Antes de comprarar las matrices se binarizan con el umbral Umbral. A>Umbral, B>Umbral. Más...

double	Pds::Matrix::NAccuracy (const Pds::Matrix &B) const
	Calcula el valor de la Accuracy entre los elementos de las matrices A (Self) y B. Antes de comprarar las matrices se conviertena enteros con round(). Más...

double	Pds::Matrix::R2 (const Pds::Matrix &Y) const
	Calcula el coeficiente de determinación o . Más...

double	Pds::Matrix::Rf (const Pds::Matrix &Y) const
	Calcula o . Más...

double	Pds::Matrix::Mape (const Pds::Matrix &B) const
	Calcula el error absoluto medio porcentual (Mean Absolute Percentage Error) de una matriz. Más...

Métodos Information theory
Herramientas genéricas
double	Pds::Matrix::InformationGain (const std::vector< Pds::Matrix > &A, double Umbral=0.5) const
	Retorna el Information Gain entre si mismo B y {A[0],A[1],...,A[N-1]}. Antes de comprarar las matrices se binarizan con el umbral Umbral. A[n]>Umbral, B>Umbral. Más...

double	Pds::Matrix::BinaryEntropy (double umbral) const
	Calcula la entropia binaria de la estadistica de y , la probabilidade de unos y ceros en la matriz despues de ubralizar con >=umbral. Más...

double	Pds::Matrix::P1Probability (double umbral) const
	Calcula la probabilidad binaria , la probabilidade en relación a los unos y ceros en la matriz despues de ubralizar con >=umbral. Más...

Pds::Matrix	Pds::Matrix::BalancedBinaryWeight (double umbral) const
	Retorna una matriz de pesos para balancear la cantidad de 1s y 0s en la matriz. Los unos y ceros en la matriz son obtenidos despues de ubralizar con >=umbral. Más...

Métodos Digital Signal Processing
Herramientas genéricas
Pds::Vector	Pds::Matrix::HistogramIntNorm (int min=0, int max=255) const
	Retorna un vector con el histograma de elementos, desde `min` hasta `max` (valores enteros). Elementos con valores `round(val)` menores a min o mayores a max no son computados en el histograma. Más...

Pds::Vector	Pds::Matrix::Histogram (double min, double max, unsigned int L) const
	Retorna un vector con um histograma de elementos espaciados $\delta$ . Elementos con valores menores a $min-\frac{\delta}{2}$ o mayores a $max+\frac{\delta}{2}$ no son computados en el histograma. Más...

Pds::Vector	Pds::Matrix::Histogram (unsigned int L) const
	Retorna un vector con um histograma de elementos espaciados $\delta$ . Elementos con valores menores a o mayores a no son computados en el histograma. Más...

double	Pds::Matrix::Corr (const Pds::Matrix &B) const
	Calcula la correlación de Pearson con la matriz. Más...

double	Pds::Matrix::Cov (const Pds::Matrix &B) const
	Calcula la covarianza con la matriz. Más...

Pds::Matrix	Pds::Matrix::CovMatrix (void) const
	Calcula la matriz de covarianza de la matriz. Más...

Pds::Matrix	Pds::Matrix::CovMatrix (Pds::Matrix &Mean) const
	Calcula la matriz de covarianza de la matriz. Más...

Pds::Matrix	Pds::Matrix::XCorr (const Pds::Matrix &B, bool Same=false) const
	Calcula la correlacion cruzada entre A y B. Más...

Pds::Matrix	Pds::Matrix::Conv (const Pds::Matrix &B, Pds::Ra::Padding Padding=Pds::Ra::Full) const
	Calcula la convolución entre A y B. Más...

static Pds::Size	Pds::Matrix::Conv2DOutputSize (const Pds::Size &A, const Pds::Size &B, const std::vector< unsigned int > &Strides, Pds::Ra::Padding Padding)
	Calcula el tamaño de la matriz resultado de la convolucion de A y B. Más...

Pds::Matrix	Pds::Matrix::Conv2D (const Pds::Matrix &B, const std::vector< unsigned int > &Strides={1, 1}, Pds::Ra::Padding Padding=Pds::Ra::Full) const
	Calcula la convolución entre A y B. Más...

bool	Pds::Matrix::Conv2D (const Pds::Matrix &B, Pds::Matrix &C, const std::vector< unsigned int > &Strides={1, 1}, Pds::Ra::Padding Padding=Pds::Ra::Full) const
	Calcula la convolución entre A y B. Más...

Pds::Matrix	Pds::Matrix::MaxPooling (unsigned int LinPool, unsigned int ColPool) const
	Aplica max pooling de la matriz $\mathbf{A}$ de $L_\mathbf{A}$ lineas y $C_\mathbf{A}$ columnas. Más...

Pds::Matrix	Pds::Matrix::FilterMean (unsigned int r) const
	Procesa la matriz A usando un filtro mean de radio r. Más...

Pds::Matrix	Pds::Matrix::FilterMean3 (void) const
	Procesa la matriz A usando un filtro mean de radio 1. Más...

Pds::Matrix	Pds::Matrix::Resize (double factor) const
	Retorna una matriz B (size: NlinB,NcolB) resultado de aplicar un subsampling de la matriz A (size: Nlin,Ncol) por un factor. Más...

Métodos de álgebra lineal
Herramientas genéricas
bool	Pds::Matrix::QR (Pds::Matrix &Q, Pds::Matrix &R) const
	Calcula la descomposición QR de una matriz $A \in \mathrm{R}^{M \times N}$ . Más...

Pds::Matrix	Pds::Matrix::CholeskyBanachiewicz (void) const
	Dada una matriz simétrica definida positiva $\mathbf{A}$ , este método realiza la descomposición Cholesky, especificamente Cholesky-Banachiewicz. Más...

Pds::Matrix	Pds::Matrix::CholeskyCrout (void) const
	Dada una matriz simétrica definida positiva $\mathbf{A}$ , este método realiza la descomposición Cholesky, especificamente Cholesky-Crout. Más...

Pds::Matrix	Pds::Matrix::HessenbergReduction (void) const
	Dada una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ , este metodo retorna una Matriz de Hessenberg ( $\mathbf{H} \in \mathrm{R}^{N \times N}$ ) semejante a la matriz $\mathbf{A}$ . La matriz $\mathbf{H}$ es calculada siguiendo la Householder transformation. Más...

Pds::Matrix	Pds::Matrix::SubLambdaI (double lambda) const
	Dada una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ , este metodo retorna : Más...

Pds::Matrix	Pds::Matrix::AddLambdaI (double lambda) const
	Dada una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ , este metodo retorna : Más...

double	Pds::Matrix::QuadraticForm (const Pds::Vector &x) const
	Calcula la forma cuadrática $\mathbf{x}^{T} \mathbf{A} \mathbf{x}$ . Más...

Pds::Vector	Pds::Matrix::QuadraticFormWithRows (const Pds::Matrix &X) const
	Calcula la forma cuadrática $\mathbf{x}_{l}^{T} \mathbf{A} \mathbf{x}_{l}$ . Más...

Pds::Vector	Pds::Matrix::QuadraticFormWithRows (const Pds::Matrix &X, const Pds::Vector &Mu) const
	Calcula la forma cuadrática $\mathbf{x}_{l}^{T} \mathbf{A} \mathbf{x}_{l}$ . Más...

Pds::Matrix	Pds::Matrix::QuadraticFormWithSamples (const std::vector< Pds::Matrix > &X, const Pds::Vector &Mu) const
	Calcula la forma cuadrática $\mathbf{x}_{l}^{T} \mathbf{A} \mathbf{x}_{l}$ . Más...

Pds::Vector	Pds::Matrix::QuadraticDotWithRows (const Pds::Vector &Mu) const
	Calcula la forma cuadrática $\mathbf{x}_{l}^{T} \mathbf{x}_{l}$ . Más...

double	Pds::Matrix::MaxAbsOfLowerTriangular (void) const
	Retorna el máximo valor absoluto de los elementos abajo de la diagonal. La matriz no necesita ser cuadrada, lo elementos abajo de la diagonal se revisan hasta donde se pueda. Más...

double	Pds::Matrix::MaxAbsOfDiag (void) const
	Retorna el máximo valor absoluto de la diagonal de una matriz $\mathbf{A}$ . La matriz no necesita ser cuadrada, la diagonal se revisa hasta donde se pueda. Más...

double	Pds::Matrix::MinAbsOfDiag (void) const
	Retorna el mínimo valor absoluto de la diagonal de una matriz $\mathbf{A}$ . La matriz no necesita ser cuadrada, la diagonal se revisa hasta donde se pueda. Más...

double	Pds::Matrix::MinOfDiag (void) const
	Retorna el valor mínimo de la diagonal de una matriz cuadrada $\mathbf{A}$ . Más...

double	Pds::Matrix::Det (void) const
	Calcula la determinante. Más...

double	Pds::Matrix::Dot (const Pds::Matrix &B) const
	Calcula el producto punto entre dos matrices. Más...

double	Pds::Matrix::RMS (void) const
	Calcula valor raiz quadrático medio de una matriz. Más...

double	Pds::Matrix::MeanAbsolute (void) const
	Calcula valor absoluto medio de una matriz. Más...

double	Pds::Matrix::MeanSquare (void) const
	Calcula valor quadrático medio de una matriz. Más...

double	Pds::Matrix::MSE (const Pds::Matrix &B) const
	Calcula valor del error quadrático medio (Mean Square Error) entre las matrices y . Más...

double	Pds::Matrix::RMSE (const Pds::Matrix &B) const
	Calcula valor de la raiz cuadrada del error quadrático medio (Root Mean Square Error) entre las matrices y . Más...

double	Pds::Matrix::PSNR (const Pds::Matrix &B, unsigned int NBITS) const
	Calcula valor del error quadrático medio entre las matrices y . Más...

double	Pds::Matrix::SumSquare (void) const
	Calcula valor de la suma quadrática de una matriz. Más...

Pds::Vector	Pds::Matrix::SumSquareInRows (void) const
	Calcula la suma cuadrada de cada linea de la matriz. Más...

double	Pds::Matrix::NormDiff (const Pds::Matrix &B) const
	Calcula la 2-norm de una matriz (Frobenius norm). Más...

double	Pds::Matrix::NormDiff2 (const Pds::Matrix &B) const
	Calcula la 2-norm al cuadrado de una matriz. Más...

double	Pds::Matrix::Norm (void) const
	Calcula la 2-norm de una matriz (Frobenius norm). Más...

double	Pds::Matrix::PNorm1 (void) const
	Calcula la 1-norm de un vector. Más...

double	Pds::Matrix::PNormInf (void) const
	Calcula la inf-norm de una matriz. Más...

bool	Pds::Matrix::Normalize (void)
	Normaliza la matriz convirtiendolo en una matriz unitaria. Más...

bool	Pds::Matrix::NormalizeRows (void)
	Normaliza cada linea de la matriz convirtiendolo en una linea unitaria. Más...

Pds::Vector	Pds::Matrix::MultiIndex (const Pds::Vector &d) const
	Dada una matriz $\mathbf{X}=\left[\mathbf{x}_1,\quad \mathbf{x}_2,\quad ...,\quad \mathbf{x}_n,\quad ...,\quad \mathbf{x}_N\right]$ es calculado el vector $\mathbf{\overline{X}}^{\mathbf{d}}$ . Más...

Métodos de álgebra lineal - Eigenvalues Eigenvectors
Herramientas genéricas
Pds::Vector	Pds::Matrix::EigenValues (unsigned int MaxIter=2048, double MinFactor=0.00001, bool SortAsc=true) const
	Calcula los valores própios (Eigenvalues) de una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ siguiendo el algoritmo shift QR, El resultado en la diagonal de $\mathbf{A}^{(k+1)}$ es cargado en el vector $\boldsymbol{\lambda} \in \mathrm{R}^{N}$ . Más...

Pds::Matrix	Pds::Matrix::EigenVectors (const Pds::Vector &Lambda, unsigned int MaxIter=20000, bool EmptyWhenError=true) const
	Calcula los vectores própios (Eigenvectors) de una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ , Los vectores propios están colocados en las columnas de la matriz $\mathbf{V} \in \mathrm{R}^{N \times K}$ . Más...

Pds::Vector	Pds::Matrix::EigenVector_RegInvIter (double lambda, const Pds::Vector &v0, unsigned int MaxIter=20000, bool EmptyWhenError=true) const
	Calcula un autovector (Eigenvector) de una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ . Internamente usa version regularizada del algoritmo Inverse iteration Más...

Pds::Vector	Pds::Matrix::EigenDominant (double &lambda, unsigned int MaxIter=20000) const
	Calcula el autovector (Eigenvector) y el autovalor (Eigenvalue) dominante en una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ . Internamente usa el algoritmo Power iteration Más...

Métodos para find
Herramientas genéricas
std::vector< unsigned int >	Pds::Matrix::Find (void) const
	Retorna una lista de indices donde existe un 1 en la matriz A. Más...

std::vector< unsigned int >	Pds::Matrix::FindIdOfKMin (unsigned int K) const
	Retorna un vector de indices de los K menores valores en la matriz A. Más...

std::vector< unsigned int >	Pds::Matrix::FindIdOfKMin (unsigned int K, std::vector< double > &dat) const
	Retorna un vector de indices de los K menores valores en la matriz A. Más...

Pds::Matrix	Pds::Matrix::FindRows (const Pds::Vector &B, double b=0.5) const
	Retorna una nueva matriz con las lineas donde existe un 1 en la matriz B. En verdad B es binarizado internamente con (B>b). La matriz debe tener el mismo número de lineas de B caso contrario se retorna una matriz vacia. Más...

Pds::Matrix	Pds::Matrix::FindVal (double val) const
	Retorna una nueva matriz B (binaria) con unos donde exista en A el valor val, y cero donde no se cumpla esta condición. Más...

bool	Pds::Matrix::FindValAndReplace (double val, double rep)
	Remplaza valores especificos por una matriz por otros. Más...

std::vector< Pds::Matrix >	Pds::Matrix::FindRowsBlock (const Pds::Vector &V) const
	Retorna un vector de matrices con las lineas donde existe un mismo id en el vector . En verdad es convertido a entero usando la función round(). La matriz debe tener el mismo número de lineas de caso contrario se retorna una matriz vacia. Más...

std::vector< Pds::Matrix >	Pds::Matrix::FindRowsBlock (const Pds::Vector &V, std::vector< int > &Label) const
	Retorna un vector de matrices con las lineas donde existe un mismo id en el vector . En verdad es convertido a entero usando la función round(). La matriz debe tener el mismo número de lineas de caso contrario se retorna una matriz vacia. Más...

std::vector< Pds::Matrix >	Pds::Matrix::FindRowsBlock (const Pds::Array< unsigned int > &ID) const
	Retorna un grupo de matrices con las lineas donde existe el mismo indice id en la matriz entera . La matriz debe tener el mismo número de lineas que elementos en caso contrario se retorna una matriz vacia. Más...

Métodos para aplicar operaciones
Herramientas genéricas
bool	Pds::Matrix::Apply (const Pds::Matrix &B)
	Aplica la función func a cada elemento de la matriz. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada. Más...

bool	Pds::Matrix::Apply (double Alpha, const Pds::Matrix &B)
	Aplica la función func a cada elemento de la matriz. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada. Más...

bool	Pds::Matrix::Apply (double(*func)(double))
	Aplica la función func a cada elemento de la matriz. Más...

bool	Pds::Matrix::Apply (double(*func)(double), const Pds::Matrix &B)
	Aplica la función func a cada elemento de la matriz. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada. Más...

bool	Pds::Matrix::Apply (double(*func)(double, double), double var)
	Aplica la función func a cada elemento de la matriz. Más...

bool	Pds::Matrix::Apply (double(*func)(double, const std::vector< double > &), const std::vector< double > &var)
	Aplica la función func a cada elemento de la matriz. Más...

bool	Pds::Matrix::ApplyAdd (double(*func)(double), double alpha, const Pds::Matrix &B, double beta, const Pds::Matrix &C)
	Aplica la función func a cada elemento de la suma ponderada de las matrices. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada. Más...

bool	Pds::Matrix::ApplyAdd (double alpha, const Pds::Matrix &B, double beta, const Pds::Matrix &C)
	Aplica la función func a cada elemento de la suma ponderada de las matrices. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada. Más...

bool	Pds::Matrix::ApplySub (double(*func)(double), const Pds::Matrix &B, const Pds::Matrix &C)
	Aplica la función func a cada elemento de la diferencia de matrices. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada. Más...

bool	Pds::Matrix::ApplySub (const Pds::Matrix &B, const Pds::Matrix &C)
	Aplica a cada elemento de la diferencia de matrices. La matriz que recibe debe tener el mismo tamaño que las matrices de entrada. Más...

bool	Pds::Matrix::ApplyProduct (const Pds::Matrix &B, const Pds::Matrix &C)
	[Elemento a elemento] Aplica a cada elemento de la multiplicación de matrices. La matriz que recibe debe tener el mismo tamaño que las matrices de entrada. Más...

bool	Pds::Matrix::ApplyInCol (unsigned int col, double(*func)(double))
	Aplica la función func a cada elemento de la columna col de la matriz. Más...

bool	Pds::Matrix::ApplyInCol (unsigned int col, double(*func)(double, double), double var)
	Aplica la función func a cada elemento de la columna col de la matriz. Más...

Métodos para operar Pds::Matrix
Herramientas genéricas
Pds::Matrix	Pds::Matrix::OperateRows (double(*func)(const Pds::Matrix &Row)) const
	Opera la función func usando como entrada cada fila de la matriz. Más...

Pds::Matrix	Pds::Matrix::OperateRows (double(*func)(const Pds::Vector &Row)) const
	Opera la función func usando como entrada cada fila de la matriz. Más...

Pds::Matrix	Pds::Matrix::OperateRows (double(*func)(const Pds::Vector &Row, const Pds::Vector &C), const Pds::Vector &C) const
	Opera la función func usando como entrada cada fila de la matriz. Más...

Pds::Matrix	Pds::Matrix::OperateRows (double(*func)(const Pds::Vector &Row, const Pds::Vector &C, const std::vector< double > &var), const Pds::Vector &C, const std::vector< double > &var) const
	Opera la función func usando como entrada cada fila de la matriz. Más...

Pds::Matrix	Pds::Matrix::OperateCols (double(*func)(const Pds::Matrix &Col)) const
	Opera la función func usando como entrada cada columna de la matriz. Más...

Pds::Matrix	Pds::Matrix::OperateCols (double(*func)(const Pds::Vector &Col)) const
	Opera la función func usando como entrada cada columna de la matriz. Más...

Pds::Matrix	Pds::Matrix::OperateCols (double(*func)(const Pds::Vector &Col, const Pds::Vector &C), const Pds::Vector &C) const
	Opera la función func usando como entrada cada columna de la matriz. Más...

Pds::Matrix	Pds::Matrix::TransformRows (Pds::Vector(*func)(const Pds::Vector &Row, const Pds::Vector &C), const Pds::Vector &C) const
	Opera la función func usando como entrada cada fila de la matriz. Más...

Pds::Matrix	Pds::Matrix::Scale (double minval, double maxval) const
	Rescala linearmente los datos desde minval a maxval. Más...

Pds::Matrix	Pds::Matrix::Round (unsigned int decimal=0) const
	Retorna una matriz con los valores redondeados. Más...

Métodos con regiones con Pds::Matrix.
Herramientas genéricas
bool	Pds::Matrix::CopyRegion (const Pds::RegionRect &Rin, const Pds::RegionRect &Rout, Pds::Matrix &Mout) const
	Copia la región Rin de la matriz a la región Rout de la matriz Mout. Más...

bool	Pds::Matrix::InitRegion (Pds::RegionRect R, double val)
	Inicializa la región R de la matriz con el valor val. Más...

Pds::RegionRect	Pds::Matrix::GetRegion (void) const
	Retorna una variable Pds::RegionRect desde la posicion (0,0), con ancho y alto (Mat.Nlin(),Mat.Ncol()). Más...

bool	Pds::Matrix::MeanOfRegion (const Pds::RegionRect &Rin, double *mean) const
	Calcula la media de los elementos en la region, pero para que sea calculado debe existir una interseccion diferente de zero con la matriz. Los valores fuera de la matriz son considerados cero. Más...

double	Pds::Matrix::MeanOfRegion (const Pds::RegionRect &Rin) const
	Calcula la media de los elementos en la region, pero para que sea calculado debe existir una interseccion diferente de zero con la matriz. Los valores fuera de la matriz son considerados cero. Más...

bool	Pds::Matrix::MeanSquareOfRegion (const Pds::RegionRect &Rin, double *mean) const
	Calcula la media del cuadrado de los elementos en la region, pero para que sea calculado debe existir una interseccion diferente de zero con la matriz. Los valores fuera de la matriz son considerados cero. Más...

double	Pds::Matrix::MeanSquareOfRegion (const Pds::RegionRect &Rin) const
	Calcula la media del cuadrado de los elementos en la region, pero para que sea calculado debe existir una interseccion diferente de zero con la matriz. Los valores fuera de la matriz son considerados cero. Más...

bool	Pds::Matrix::StdAndMeanOfRegion (const Pds::RegionRect &Rin, double std, double mean) const
	Calcula el desvío padrón y la media de los elementos de la intersección de la región con la matriz. Más...

bool	Pds::Matrix::CorrNormRegions (const Pds::Matrix &M1, const Pds::RegionRect &R0, const Pds::RegionRect &R1, double *corrn) const
	Calcula correlación normalizada entre los elementos de la intersección de la regiones con sus matrices. Más...

bool	Pds::Matrix::CorrNormRegions (const Pds::Matrix &M1, const Pds::RegionRect &R0, const Pds::RegionRect &R1, double means0, double means1, double *corrn) const
	Calcula correlación normalizada entre los elementos de la intersección de la regiones con sus matrices. Más...

bool	Pds::Matrix::CorrPearsonRegions (const Pds::Matrix &M1, const Pds::RegionRect &R0, const Pds::RegionRect &R1, double *pcc) const
	Calcula el coeficiente de correlación de Pearson (PCC) entre los elementos de la intersección de la regiones con sus matrices. Más...

bool	Pds::Matrix::CorrPearsonRegions (const Pds::Matrix &M1, const Pds::RegionRect &R0, const Pds::RegionRect &R1, double mean0, double mean1, double std0, double std1, double *pcc) const
	Calcula el coeficiente de correlación de Pearson (PCC) entre los elementos de la intersección de la regiones con sus matrices. Más...

Métodos variados con Pds::Matrix.
Herramientas genéricas
std::string	Pds::Matrix::ToString (void) const
	Convierte los datos de la matriz en un std::string. Más...

std::string	Pds::Matrix::ToString (const std::string &EndData) const
	Convierte los datos de la matriz en un std::string. Más...

void	Pds::Matrix::Print (const std::string &str, unsigned int precision) const
	Imprime en pantalla el contenido de la matriz después del texto indicado en str. Más...

void	Pds::Matrix::Print (const std::string &str) const
	Imprime en pantalla el contenido de la matriz después del texto indicado en str. Más...

void	Pds::Matrix::Print (void) const
	Imprime en pantalla el contenido de la matriz. Más...

Métodos para reordenar memoria con Pds::Matrix.
Herramientas genéricas
void	Pds::Matrix::MakeEmpty (void)
	libera los datos internos de la matriz y la convierte en una matriz nula. es decir con lineas y columnas cero. Más...

bool	Pds::Matrix::Reshape (unsigned int Nlin, unsigned int Ncol)
	Remodela los datos internos de la array y la convierte en una array de tamaño diferente, los datos que faltan se rellenan con cero. Más...

Pds::Matrix	Pds::Matrix::Remodel (unsigned int Nlin, unsigned int Ncol)
	Remodela los datos internos de la array y retorna un array de tamaño diferente, los datos que faltan se rellenan con cero. Más...

bool	Pds::Matrix::FusionVer (std::list< Pds::Matrix > &list)
	Concatena verticalmente varias matrices. Si las matrices no tienen el mismo número de columnas se considera um error. Destruye las matrices en list. Este metodo es mas rapido que Pds::MergeVer(list) pues transplanta memoria. Más...

Métodos para exportar e importar TXT con Pds::Matrix.
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
bool	Pds::Matrix::SaveInStream (std::ofstream &myfile) const
	Escribe en un archivo de texto el contenido de la matriz. Más...

bool	Pds::Matrix::LoadFromStream (std::ifstream &ifs, unsigned int Nlin, unsigned int Ncol)
	Lee `Nlin*Ncol` elementos desde un archivo, estos elementos son colocados en una matriz de `Nlin` lineas y `Ncol` columnas. Cada elemento es separado por tabuladores y cada linea por un salto de linea. Más...

bool	Pds::Matrix::LoadLineFromStream (std::ifstream &ifs)
	Lee una linea de un archivo y crea una matriz de Nlin=1 y Ncol columnas. Cada elemento es separado por tabuladores y cada linea por un salto de linea. Más...

bool	Pds::Matrix::Save (const std::string &filepath) const
	Escribe en un archivo de texto el contenido de la matriz. Más...

bool	Pds::Matrix::Load (const std::string &filepath)
	Lee desde un archivo una matriz de Nlin lineas y Ncol columnas. Más...

Métodos para exportar e importar CSV con Pds::Matrix.
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
bool	Pds::Matrix::ExportCsvFile (const std::string &filepath, char delimitador=',') const
	Escribe en un archivo de texto el contenido de la matriz usando un formato Csv (Comma Separated Values). Más...

bool	Pds::Matrix::ExportCsvFile (const std::string &filepath, std::vector< std::string > titles, char delimitador=',') const
	Escribe en un archivo de texto el contenido de la matriz usando un formato Csv (Comma Separated Values). Más...

bool	Pds::Matrix::ImportCsvFile (const std::string &filepath, char delimitador, std::vector< std::string > &titles)
	Lee un archivo de texto el contenido de la matriz usando un formato Csv (Comma Separated Values). Más...

bool	Pds::Matrix::ImportCsvFileWithoutTitles (const std::string &filepath, char delimitador)
	Lee un archivo de texto el contenido de la matriz usando un formato Csv (Comma Separated Values). Más...

Métodos para exportar e importar TEX con Pds::Matrix.
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
bool	Pds::Matrix::ExportTexFile (const std::string &filepath, const std::vector< std::string > &titles, const std::vector< std::string > &rowtitles, const std::string &caption="My caption", const std::string &label="mylabel") const
	Escribe en un archivo de texto el contenido de la matriz usando un formato de tabla de tex. Más...

bool	Pds::Matrix::ExportTexFile (const std::string &filepath, const std::vector< std::string > &titles, const std::string &caption="My caption", const std::string &label="mylabel") const
	Escribe en un archivo de texto el contenido de la matriz usando un formato de tabla de tex. Más...

bool	Pds::Matrix::ExportTexFile (const std::string &filepath, const std::string &caption="My caption", const std::string &label="mylabel") const
	Escribe en un archivo de texto el contenido de la matriz usando un formato de tabla de tex. Más...

Métodos para exportar e importar Json con Pds::Matrix.
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
bool	Pds::Matrix::ExportJsonToStream (std::ofstream &myfile) const
	Escribe en un archivo Json el contenido de la matriz. Más...

bool	Pds::Matrix::ExportJsonToStream (std::ofstream &myfile, unsigned int ntabs) const
	Escribe en un archivo Json el contenido de la matriz. Más...

std::string	Pds::Matrix::ExportJsonToString (unsigned int ntabs) const
	Retorna una cadena de texto en formato Json con el contenido de la matriz. Más...

Pds::Json	Pds::Matrix::ToJson (void) const
	Retorna un objeto Pds::Json con el contenido de la matriz. Más...

bool	Pds::Matrix::FromJson (const Pds::Json &J)
	Lee un objeto Pds::Json busca la etiqueta "Matrix" y lo carga en la matriz. El objeto debe tener al menos los siguientes dados. Más...

Métodos para exportar e importar XML con Pds::Matrix.
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
bool	Pds::Matrix::ExportXmlToStream (std::ofstream &myfile) const
	Escribe en un archivo Xml el contenido de la matriz. Más...

bool	Pds::Matrix::ExportXmlToStringStream (std::stringstream &sstream) const
	Escribe en un `std::stringstream` en formato Xml el contenido de la matriz. Más...

std::string	Pds::Matrix::ExportXmlToString (void) const
	Retorna un `std::string` en formato Xml con el contenido de la matriz. Más...

bool	Pds::Matrix::ImportXmlFromString (const std::string &str)
	Carga el contenido de una matriz desde un `std::string` en formato Xml. Más...

Métodos para exportar en formato Octave/Matlab desde Pds::Matrix.
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
bool	Pds::Matrix::ExportMatFile (const std::string &pname, const std::string &filepath) const
	Escribe en un archivo binario en formato de octave la matriz. Es necesario dar un nombre como identificador de matriz. Más...

std::string	Pds::Matrix::ExportOctaveString (const std::string &pname) const
	Retorna un std:string con los datos de la matriz en el formato de octave. Es necesario dar un nombre como identificador de matriz. Más...

Métodos para exportar e importar BMP con Pds::Matrix.
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
bool	Pds::Matrix::ExportBmpFile (const unsigned char colormap[256][3], const std::string &filepath) const
	Escribe en una matriz en un archivo binario en formato BMP. Losdatos deben ir de 0 a 255, valores superiores o inferiores serán truncados. Más...

bool	Pds::Matrix::ExportBmpFileScale (const unsigned char colormap[256][3], const std::string &filepath) const
	Escribe en una matriz en un archivo binario en formato BMP. Escala los datos de de 0 a 255, si el valor minimo y máximo son iguales la matriz se llena con ceros. Más...

Métodos Static con procesamiento de 3 matrices.
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
static bool	Pds::Matrix::FunctionCh3ToCh3 (void(*func)(double a1, double a2, double a3, double &b1, double &b2, double &b3), const Pds::Matrix &A1, const Pds::Matrix &A2, const Pds::Matrix &A3, Pds::Matrix &B1, Pds::Matrix &B2, Pds::Matrix &B3)
	Convierte elemento a elemento 3 matrices a 3 matrices. Más...

Métodos Static con Matrices SampleBlock.
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
static bool	Pds::Matrix::IsSampleBlock (const std::vector< Pds::Matrix > &Block)
	Verifica que el bloque (std::vector<Pds::Matrix>) sea un vector no vacío de matrices no nulas y similares. Es decir un Hiperrectángulo. Más...

static Pds::Vector	Pds::Matrix::FlattenSampleBlock (const std::vector< Pds::Matrix > &Block)
	Convierte a `Pds::vector` un SampleBlock. Más...

static std::vector< Pds::Matrix >	Pds::Matrix::RandNSampleBlock (unsigned int N, const Pds::Size &Sz)
	Crea un bloque (std::vector<Pds::Matrix>) con matrices no nulas y similares inicializadas con Pds::RandN(). Más...

static std::vector< Pds::Matrix >	Pds::Matrix::ZerosSampleBlock (unsigned int N, const Pds::Size &Sz)
	Crea un bloque (std::vector<Pds::Matrix>) con matrices no nulas y similares inicializadas con Pds::Zeros(). Más...

static std::vector< Pds::Matrix >	Pds::Matrix::MaxPoolingSampleBlock (const std::vector< Pds::Matrix > &A, unsigned int LinPool, unsigned int ColPool)
	Aplica max pooling a cada matriz $\mathbf{A}[n]$ de $L_\mathbf{An}$ lineas y $C_\mathbf{An}$ columnas. Más...

static Pds::Matrix	Pds::Matrix::MeanSampleBlock (const std::vector< Pds::Matrix > &Block)
	Calcula A,la matriz media de un conjunto de N matrizes agrupadas en un std::vector. Más...

static Pds::Matrix	Pds::Matrix::GetSamples (const std::vector< Pds::Matrix > &Block)
	Convierte las muestras de un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos, en una matriz Pds::Matrix(L,N). Lee los datos de la columna actual y pasa a la siguiente, desde la columna 0. Más...

static bool	Pds::Matrix::GetSampleRaw (const std::vector< Pds::Matrix > &Block, unsigned int lin, unsigned int col, Pds::Vector &x)
	Extrae una muestra de un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos, a un vector Pds::Vector(N). Más...

static bool	Pds::Matrix::GetSampleRaw (const std::vector< Pds::Matrix > &Block, unsigned int id, Pds::Vector &x)
	Extrae una muestra de un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos, a un vector Pds::Vector(N). Más...

static Pds::Matrix	Pds::Matrix::GetSamples (const std::vector< Pds::Matrix > &Block, const std::vector< unsigned int > Id)
	Convierte M muestras de un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos, en una matriz Pds::Matrix(M,N). Más...

static std::vector< Pds::Matrix >	Pds::Matrix::ImportBmpFile (const std::string &bmpfilename)
	Lee matrices de un archivo binario en formato BMP. Más...

static Pds::Matrix	Pds::Matrix::ImportBmpFileAsGray (const std::string &bmpfilename)
	Retorna una matriz en escala de grises, de 0 a 255. Más...

static bool	Pds::Matrix::ExportBmpFile (const Pds::Matrix &R, const Pds::Matrix &G, const Pds::Matrix &B, const std::string &bmpfilename)
	Escribe en una matriz en un archivo binario en formato BMP. Losdatos deben ir de 0 a 255, valores superiores o inferiores serán truncados. Más...

static bool	Pds::Matrix::ExportAsGif (const std::vector< Pds::Matrix > &Block, const std::string &filename, unsigned int delay=100, const unsigned char colormap[256][3]=Pds::Colormap::Gray)
	Salva el bloque (std::vector<Pds::Matrix>) en una imagen GIF. Más...

static std::string	Pds::Matrix::ExportSampleBlockXmlToString (const std::vector< Pds::Matrix > &Block)
	Retorna un `std::string` en formato Xml con el contenido del SampleBlock. Más...

static std::vector< Pds::Matrix >	Pds::Matrix::ImportSampleBlockXmlFromString (const std::string &str)
	Carga el contenido de una std::vector<Pds::Matrix> desde un `std::string` en formato Xml. Más...

static bool	Pds::Matrix::ExportSampleBlockXmlToStream (std::ofstream &myfile, const std::vector< Pds::Matrix > &Block)
	Retorna un `std::string` en formato Xml con el contenido del SampleBlock. Más...

Métodos Static con Matrices BatchBlock.
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
static bool	Pds::Matrix::IsBatchBlock (const std::vector< std::vector< Pds::Matrix > > &Tensor)
	Verifica que el tensor (std::vector<std::vector<Pds::Matrix>>) sea un vector de vectores no vacíos de matrices no nulas y similares. Es decir un Hiperrectángulo. Más...

static std::vector< std::vector< Pds::Matrix > >	Pds::Matrix::RandNBatchBlock (unsigned int L, unsigned int N, const Pds::Size &Sz)
	Crea un tensor (std::vector<std::vector<Pds::Matrix>>) con matrices no nulas y similares inicializadas con Pds::RandN(). Más...

static std::vector< std::vector< Pds::Matrix > >	Pds::Matrix::ZerosBatchBlock (unsigned int L, unsigned int N, const Pds::Size &Sz)
	Crea un tensor (std::vector<std::vector<Pds::Matrix>>) con matrices no nulas y similares inicializadas con Pds::Zeros(). Más...

static std::string	Pds::Matrix::ExportBatchBlockXmlToString (const std::vector< std::vector< Pds::Matrix > > &Block)
	Retorna un `std::string` en formato Xml con el contenido del BatchBlock. Más...

static std::vector< std::vector< Pds::Matrix > >	Pds::Matrix::ImportBatchBlockXmlFromString (const std::string &str)
	Carga el contenido de una `std::vector<std::vector<Pds::Matrix>>` desde un `std::string` en formato Xml. Más...

static bool	Pds::Matrix::ExportBatchBlockXmlToStream (std::ofstream &myfile, const std::vector< std::vector< Pds::Matrix > > &Block)
	Escribe en un `std::ofstream` en formato Xml con el contenido del BatchBlock. Más...

Métodos Static con Matrices extras.
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
static Pds::Matrix	Pds::Matrix::FromString (const std::string &str)
	Convierte un sdt::string a una Matriz de Nlin lineas y Ncol columnas. Más...

Operadores unarios y sus métodos equivalentes con Pds::Matrix.
Descripción de algunos operadores habilitados a trabajar con Pds::Matrix.
Pds::Matrix	Pds::Matrix::T (void) const
	Transpuesta de si mismo (A), el resultado es cargado en B. Más...

Pds::Matrix	Pds::Matrix::MtM (void) const
	Retorna A.T()*A cargado en B. Más...

Pds::Matrix	Pds::Matrix::MtM (const Pds::Matrix &B) const
	Retorna A.T()*A cargado en B. Más...

Pds::Matrix	Pds::Matrix::MMt (void) const
	Retorna A*A.T() cargado en B. Más...

Pds::Matrix	Pds::Matrix::MMt (const Pds::Matrix &B) const
	Retorna A*A.T() cargado en B. Más...

Pds::Matrix	Pds::Matrix::Inv (double *rcond=NULL) const
	Retorna la matriz inversa. Más...

Pds::Matrix	Pds::Matrix::PInv (double *rcond=NULL) const
	Procesa esta matriz A y retorna B la matriz pseudo inversa de Moore Penrose. Más...

Pds::Matrix	Pds::Matrix::operator- (void) const
	Cambia de signo a si mismo (A), el resultado es cargado en B. Este operador es similar al método unario Minus. Más...

Pds::Matrix	Pds::Matrix::Minus (void) const
	Cambia de signo a si mismo (A), el resultado es cargado en B. Este método es similar al operador unario -. Más...

Pds::Matrix	Pds::Matrix::operator+ (void) const
	Asigna el signo + a si mismo (A), el resultado es cargado en B. Este operador es similar al método unario Plus. Más...

Pds::Matrix	Pds::Matrix::Plus (void) const
	Asigna el signo + a si mismo (A), el resultado es cargado en B. Este método es similar al operador unario +. Más...

Operadores binarios y sus métodos equivalentes con Pds::Matrix.
Descripción de algunos operadores habilitados a trabajar con Pds::Matrix.
Pds::Matrix	Pds::Matrix::operator* (double b) const
	Multiplica con sigo mismo (A), un valor b y el resultado es cargado en C. Este operador es similar al método Mul() Más...

Pds::Matrix	Pds::Matrix::operator* (const Pds::Matrix &B) const
	Multiplica con sigo mismo (A), una matriz B y el resultado es cargado en C. Este operador es similar al método Mul() Más...

Pds::Matrix	Pds::Matrix::Mul (double b) const
	Multiplica con sigo mismo (A), un valor b y el resultado es cargado en C. Este método es similar al operador *. Más...

Pds::Matrix	Pds::Matrix::Mul (const Pds::Matrix &B) const
	Multiplica con sigo mismo (A), una matriz B y el resultado es cargado en C. Este método es similar al operador *. Más...

bool	Pds::Matrix::Mul (const Pds::Matrix &B, Pds::Matrix &Out) const
	Multiplica con sigo mismo (A), una matriz B y el resultado es cargado en Out. Este método es similar al operador *. Más...

Pds::Matrix	Pds::Matrix::Mul (const Pds::Vector &B) const
	Multiplica con sigo mismo (A), un vector B y el resultado es cargado en C. Este método es similar al operador *. Más...

Pds::Matrix	Pds::Matrix::MulRowMatrix (const Pds::Matrix &B) const
	[Elemento a elemento] Multiplica con sigo mismo (A), una matriz B linea y el resultado es cargado en C. La unica linea de B es Multiplicada a cada linea de A. Más...

Pds::Matrix	Pds::Matrix::MulComp (double b, const Pds::Vector &B) const
	Multiplica con sigo mismo (A), un vector [b;B] y el resultado es cargado en C. Más...

Pds::Matrix	Pds::Matrix::CompMul (double b, const Pds::Matrix &B) const
	Multiplica con sigo mismo (A), previa composición, una matriz B y el resultado es cargado en C. El valor b es colocado en toda una columna. Más...

bool	Pds::Matrix::MulComp (double b, const Pds::Vector &B, Pds::Vector &Out) const
	Multiplica con sigo mismo (A), un vector [b;B] y el resultado es cargado en Out. Este método es similar al operador *. Más...

bool	Pds::Matrix::MulComp (double b, const Pds::Matrix &B, Pds::Matrix &Out) const
	Multiplica con sigo mismo (A), un vector [b;B] y el resultado es cargado en Out. Este método es similar al operador *. Más...

Pds::Matrix	Pds::Matrix::MulT (const Pds::Matrix &B) const
	Multiplica con sigo mismo (A), la transpuesta de una matriz B y el resultado es cargado en C. Este método es similar al operador *. Más...

Pds::Matrix	Pds::Matrix::TMul (const Pds::Matrix &B) const
	Multiplica con la transpuesta de sí mismo (A^T), la matriz B y el resultado es cargado en C. Este método es similar al operador *. Más...

Pds::Matrix	Pds::Matrix::operator+ (double b) const
	[Elemento a elemento] Suma con sigo mismo (A), un valor b y el resultado es cargado en C. Este operador es similar al método Add() Más...

Pds::Matrix	Pds::Matrix::operator+ (const Pds::Matrix &B) const
	[Elemento a elemento] Suma con sigo mismo (A), una matriz B y el resultado es cargado en C. Este operador es similar al método Add() Más...

Pds::Matrix	Pds::Matrix::Add (double b) const
	[Elemento a elemento] Suma con sigo mismo (A), una valor b y el resultado es cargado en C. Este método es similar al operador + Más...

Pds::Matrix	Pds::Matrix::Add (const Pds::Matrix &B) const
	[Elemento a elemento] Suma con sigo mismo (A), una matriz B y el resultado es cargado en C. Este metodo es similar al operador + Más...

Pds::Matrix	Pds::Matrix::operator- (double b) const
	[Elemento a elemento] Resta con sigo mismo (A), un valor b y el resultado es cargado en C. Este operador es similar al método Sub() Más...

Pds::Matrix	Pds::Matrix::operator- (const Pds::Matrix &B) const
	[Elemento a elemento] Resta con sigo mismo (A), una matriz B y el resultado es cargado en C. Este operador es similar al método Sub Más...

Pds::Matrix	Pds::Matrix::Sub (double b) const
	[Elemento a elemento] Resta con sigo mismo (A), una valor b y el resultado es cargado en C. Este método es similar al operador - Más...

Pds::Matrix	Pds::Matrix::Sub (const Pds::Matrix &B) const
	[Elemento a elemento] Resta con sigo mismo (A), una matriz B y el resultado es cargado en C. Este método es similar al operador - Más...

Pds::Matrix	Pds::Matrix::AddRowMatrix (const Pds::Matrix &B) const
	Suma con sigo mismo (A), una matriz B linea y el resultado es cargado en C. La unica linea de B es sumada a cada linea de A. Más...

Pds::Matrix	Pds::Matrix::SubRowMatrix (const Pds::Matrix &B) const
	Resta con sigo mismo (A), una matriz B linea y el resultado es cargado en C. La unica linea de B es restada a cada linea de A. Más...

Pds::Matrix	Pds::Matrix::operator/ (double b) const
	[Elemento a elemento] Divide con sigo mismo (A), un valor b y el resultado es cargado en C. Este operador es similar al método Div() Más...

Pds::Matrix	Pds::Matrix::operator/ (const Pds::Matrix &B) const
	[Elemento a elemento] Divide con sigo mismo (A), elemento a elemento, una matriz B y el resultado es cargado en C. Este método es similar al método .Div() Más...

Pds::Matrix	Pds::Matrix::Div (double b) const
	[Elemento a elemento] Divide con sigo mismo (A), un valor b y el resultado es cargado en C. Este método es similar al operador / Más...

Pds::Matrix	Pds::Matrix::Div (const Pds::Matrix &B) const
	[Elemento a elemento] Divide con sigo mismo (A), elemento a elemento, una matriz B y el resultado es cargado en C. Este método es similar al operador / Más...

Pds::Matrix	Pds::Matrix::DivRowMatrix (const Pds::Matrix &B) const
	[Elemento a elemento] Divide con sigo mismo (A), una matriz B linea y el resultado es cargado en C. La unica linea de B es dividida a cada linea de A. Más...

Pds::Matrix	Pds::Matrix::DivBelow (double b) const
	[Elemento a elemento] Divide con sigo mismo (A), un valor b y el resultado es cargado en C. Este método es similar al operador / Más...

Pds::Matrix	Pds::Matrix::operator& (const Pds::Matrix &B) const
	[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz B y el resultado es cargado en C. Este método es similar al método .Product() Más...

Pds::Matrix	Pds::Matrix::Product (const Pds::Matrix &B) const
	[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz B y el resultado es cargado en C. Este método es similar al operador & Más...

Pds::Matrix	Pds::Matrix::Product (double(*func)(double), const Pds::Matrix &B) const
	[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz func(B) y el resultado es cargado en C. Este método es similar al operador & Más...

Pds::Matrix	Pds::Matrix::Pow (const Pds::Matrix &B) const
	[Elemento a elemento]Potencia asi mismo (A), elemento a elemento, con una matriz B y el resultado es cargado en C. Este método es similar al operador Más...

Pds::Matrix	Pds::Matrix::Pow (double val) const
	[Elemento a elemento] Potencia asi mismo (A), elemento a elemento, con un valor val y el resultado es cargado en C. Este método es similar al operador Más...

Pds::Matrix	Pds::Matrix::GreaterThan (double b) const
	[Elemento a elemento] Calcula con sigo mismo (A), si (A) es mayor que un valor b y el resultado es cargado en C. Este método es similar al operador > Más...

Pds::Matrix	Pds::Matrix::Geq (double b) const
	[Elemento a elemento] Calcula con sigo mismo (A), si (A) es mayor o igual que un valor b y el resultado es cargado en C. Este método es similar al operador >= Más...

Pds::Matrix	Pds::Matrix::Geq (Pds::Matrix B) const
	[Elemento a elemento] Calcula con sigo mismo (A), si (A) es mayor que un valor (B) y el resultado es cargado en C. Este método es similar al operador >= Más...

Pds::Matrix	Pds::Matrix::Leq (double b) const
	[Elemento a elemento] Calcula con sigo mismo (A), si (A) es menor que un valor b y el resultado es cargado en C. Este método es similar al operador <= Más...

Pds::Matrix	Pds::Matrix::Leq (const Pds::Matrix &B) const
	[Elemento a elemento] Calcula con sigo mismo (A), si (A) es menor que un valor B y el resultado es cargado en C. Este método es similar al operador <= Más...

Pds::Matrix	Pds::Matrix::EqualTo (double b) const
	[Elemento a elemento] Calcula con sigo mismo (A), si (A) es identico a un valor b y el resultado es cargado en C. Este método es similar al operador == Más...

Pds::Matrix	Pds::Matrix::EqualTo (const Pds::Matrix &B) const
	[Elemento a elemento] Calcula con sigo mismo (A), si (A) es identico a un valor B y el resultado es cargado en C. Este método es similar al operador == Más...

Pds::Matrix	Pds::Matrix::NotEqualTo (double b) const
	[Elemento a elemento] Calcula con sigo mismo (A), si (A) no es identico a un valor b y el resultado es cargado en C. Este método es similar al operador != Más...

Pds::Matrix	Pds::Matrix::NotEqualTo (const Pds::Matrix &B) const
	[Elemento a elemento] Calcula con sigo mismo (A), si (A) no es identico a un valor B y el resultado es cargado en C. Este método es similar al operador != Más...

Pds::Matrix	Pds::Matrix::EqualToInf (void) const
	Verifica si la matriz tiene elementos con valores infinitos. Más...

Pds::Matrix	Pds::Matrix::EqualToNan (void) const
	Verifica si la matriz tiene elementos con valores NAN (Not A Number). Más...

Pds::Matrix	Pds::Matrix::EqualToFinite (void) const
	Verifica si la matriz tiene elementos con valores finitos (no +inf, no -inf y no NAN). Más...

Pds::Matrix	Pds::Matrix::Xor (const Pds::Matrix &B, double Umbral=0.5) const
	[Elemento a elemento] Xor con sigo mismo (A), una matriz B y el resultado es cargado en C. Más...

Pds::Matrix	Pds::Matrix::And (const Pds::Matrix &B, double Umbral=0.5) const
	[Elemento a elemento] And con sigo mismo (A), una matriz B y el resultado es cargado en C. Más...

Pds::Matrix	Pds::Matrix::Or (const Pds::Matrix &B, double Umbral=0.5) const
	[Elemento a elemento] Or con sigo mismo (A), una matriz B y el resultado es cargado en C. Más...

Operadores binarios acumuladores y sus métodos equivalentes con Pds::Matrix.
Descripción de algunos operadores habilitados a trabajar con Pds::Matrix.
Pds::Matrix &	Pds::Matrix::operator-= (double b)
	Resta y acumula en si mismo (A), un valor b. Este operador es similar al método SubAssig() Más...

Pds::Matrix &	Pds::Matrix::operator-= (const Pds::Matrix &B)
	Resta y acumula en si mismo (A), una matriz B. Este operador es similar al método SubAssig() Más...

bool	Pds::Matrix::SubAssig (double b)
	Resta y acumula en si mismo (A), un valor b. Este es similar al operador -=. Más...

bool	Pds::Matrix::SubAssig (const Pds::Matrix &B)
	Resta y acumula en si mismo (A), una matriz B. Este es similar al operador -=. Más...

bool	Pds::Matrix::SubAssig (double beta, const Pds::Matrix &B)
	Resta y acumula en si mismo (A), una matriz B. Este es similar al operador -=. Más...

Pds::Matrix &	Pds::Matrix::operator+= (double b)
	Suma y acumula en si mismo (A), un valor b. Este operador es similar al método AddAssig() Más...

Pds::Matrix &	Pds::Matrix::operator+= (const Pds::Matrix &B)
	Suma y acumula en si mismo (A), una matriz B. Este operador es similar al método AddAssig() Más...

bool	Pds::Matrix::AddAssig (double b)
	Suma y acumula en si mismo (A), un valor b. Este es similar al perador +=. Más...

bool	Pds::Matrix::AddAssig (const Pds::Matrix &B)
	Suma y acumula en si mismo (A), una matriz B. Este es similar al perador +=. Más...

bool	Pds::Matrix::AddAssigColMatrix (const Pds::Matrix &B)
	Suma y acumula en si mismo (A) e en cada columna, una matriz columna B. Más...

bool	Pds::Matrix::AddAssig (double alpha, const Pds::Matrix &B)
	Suma y acumula en si mismo (A), una matriz B. Más...

bool	Pds::Matrix::AddAssig (double alpha, double beta, const Pds::Matrix &B)
	Suma y acumula en si mismo (A), una matriz B. Más...

bool	Pds::Matrix::AddAssig (double alpha, const Pds::Matrix &B, double beta, const Pds::Matrix &C)
	Suma y acumula en si mismo (A), una matriz B. Más...

bool	Pds::Matrix::AddAssigAt (unsigned int lin, unsigned int col, const Pds::Matrix &B)
	Suma y acumula en si mismo (A), una matriz B desde un punto (lin,col) haciendo una intersección. Más...

bool	Pds::Matrix::AddAssigAt (unsigned int lin, unsigned int col, double b)
	Suma y acumula en si mismo (A), un valor b en un punto (lin,col) Más...

void	Pds::Matrix::AddRawAssigAt (unsigned int lin, unsigned int col, double b)
	Suma y acumula en si mismo (A), un valor b en un punto (lin,col) Más...

bool	Pds::Matrix::XorAssig (const Pds::Matrix &B, double Umbral=0.5)
	Xor y acumula en si mismo (A), una matriz B. Más...

bool	Pds::Matrix::XorAssigAt (unsigned int lin, unsigned int col, const Pds::Matrix &B, double Umbral=0.5)
	Xor y acumula en si mismo (A), una matriz B desde un punto (lin,col) haciendo una intersección. Más...

bool	Pds::Matrix::OrAssigAt (unsigned int lin, unsigned int col, const Pds::Matrix &B, double Umbral=0.5)
	Or y acumula en si mismo (A), una matriz B desde un punto (lin,col) haciendo una intersección. Más...

bool	Pds::Matrix::AndAssigAt (unsigned int lin, unsigned int col, const Pds::Matrix &B, double Umbral=0.5)
	And y acumula en si mismo (A), una matriz B desde un punto (lin,col) haciendo una intersección. Más...

bool	Pds::Matrix::XorAssigVectorAtCol (unsigned int col, const Pds::Vector &B, double Umbral=0.5)
	Xor y acumula en si mismo (A), una matriz B desde un punto (0,col) haciendo una intersección. Más...

bool	Pds::Matrix::ProductAssig (double b)
	Multiplica con sigo mismo (A), un valor b y el resultado es cargado en A. Más...

bool	Pds::Matrix::ProductAssig (const Pds::Matrix &B)
	[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz B y el resultado es cargado en A. Más...

bool	Pds::Matrix::ProductAssig (double(*func)(double), const Pds::Matrix &B)
	[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz func(B) y el resultado es cargado en A. Más...

bool	Pds::Matrix::ProductAssigMinus (double b, const Pds::Matrix &B)
	[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz (b-B) y el resultado es cargado en A. Más...

bool	Pds::Matrix::ProductAssigMinus (const Pds::Matrix &B, double b)
	[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz (B-b) y el resultado es cargado en A. Más...

bool	Pds::Matrix::ProductAssigPlus (double b, const Pds::Matrix &B)
	[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz (b+B) y el resultado es cargado en A. Más...

Pds::Matrix &	Pds::Matrix::operator*= (double b)
	Multiplica y acumula en si mismo (A), un valor b. Este operador es similar al método MulAssig() Más...

Pds::Matrix &	Pds::Matrix::operator*= (const Pds::Matrix &B)
	Multiplica y acumula en si mismo (A), una matriz B. Este operador es similar al método MulAssig() Más...

bool	Pds::Matrix::MulAssig (double b)
	Multiplica y acumula en si mismo (A), un valor b. Este es similar al operador *=. Más...

bool	Pds::Matrix::MulAssig (const Pds::Matrix &B)
	Multiplica y acumula en si mismo (A), una matriz B. Este es similar al operador *=. Más...

Pds::Matrix &	Pds::Matrix::operator/= (const Pds::Matrix &B)
	[Elemento a elemento] Divide y acumula en si mismo (A), una matriz B. Este operador es similar al método DivAssig() Más...

bool	Pds::Matrix::DivAssig (const Pds::Matrix &B)
	Divide y acumula en si mismo (A), una matriz B. Este es similar al operador /=. Más...

bool	Pds::Matrix::DivBelowAssig (double b)
	[Elemento a elemento] Divide y acumula en si mismo (A), un valor b. Más...

Pds::Matrix &	Pds::Matrix::operator= (const Pds::Matrix &B)
	Copia en si mismo (A), una matriz B. Este operador es similar al método Copy(). No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos es reservado. Más...

bool	Pds::Matrix::Copy (const Pds::Matrix &B)
	Copia en si mismo (A), el contenido de una matriz B. Este método es similar a usar el operador = . No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos es reservado. Más...

Pds::Matrix &	Pds::Matrix::operator= (double val)
	Copia en si mismo (A), el valor val. Este operador es similar al método Copy(). No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos de 1x1 es reservado. Más...

bool	Pds::Matrix::Copy (double val)
	Copia en si mismo (A), el valor val. Este método es similar a usar el operador = . No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos de 1x1 es reservado. Más...

template<class Datum >
Pds::Matrix &	Pds::Matrix::operator= (const Pds::Array< Datum > &B)
	Copia en si mismo (A), una array B. Este operador es similar al método Copy(). No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos es reservado. Más...

template<class Datum >
bool	Pds::Matrix::Copy (const Pds::Array< Datum > &B)
	Copia en si mismo (A), el contenido de una Array B. Este método es similar a usar el operador = . No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos es reservado. Más...

Métodos para calculo de kmeans y centroides con Pds::Matrix
Descripción de algunos operadores habilitados a trabajar con Pds::Matrix.
std::vector< unsigned int >	Pds::Matrix::KNearest (unsigned int K, const Pds::Vector &V, std::vector< double > &D2) const
	Calcula que linea de $\mathbf{C}\in \mathbb{R}^{M\times N}$ es mas cercana al vector $\mathbf{v}\in \mathbb{R}^{N}$ . Más...

std::vector< unsigned int >	Pds::Matrix::KNearest (unsigned int K, const Pds::Vector &V) const
	Calcula que linea de $\mathbf{C}\in \mathbb{R}^{M\times N}$ es mas cercana al vector $\mathbf{v}\in \mathbb{R}^{N}$ . Más...

Pds::Array< unsigned int >	Pds::Matrix::IdInMultipleMse (const Pds::Matrix &X) const
	Calcula que linea de $\mathbf{C}$ es mas cercana a cada linea de $\mathbf{X}\in \mathbb{R}^{L\times N}$ . Más...

Pds::Array< unsigned int >	Pds::Matrix::IdInMultipleMse (const std::vector< Pds::Matrix > &Block) const
	Calcula que linea de $\mathbf{C}$ es mas cercana a cada muestra $0 \leq (lin,col)< (Nlin, Ncol)$ en el bloque $\mathbf{Block}\in \mathbb{R}^{N\times Nlin\times Ncol}$ . Más...

Métodos Static con arrays
Herramientas genéricas que pueden ser usadas desde Pds::Matrix
static double **	Pds::Matrix::ArrayAllocate (double(*func)(double), const Pds::Matrix &A)
	crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A). Más...

static double **	Pds::Matrix::ArrayAllocate (double(*func)(double, double), const Pds::Matrix &A, double var)
	crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,var). Más...

static double **	Pds::Matrix::ArrayAllocate (double(*func)(double, double), const Pds::Matrix &A, const Pds::Matrix &B)
	crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,B). Los tamaño de A y B son similares. Más...

static double **	Pds::Matrix::ArrayAllocate (double(*func)(double, double, double), const Pds::Matrix &A, const Pds::Matrix &B, double var)
	crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,B,var). Los tamaño de A y B son similares. Más...

static double **	Pds::Matrix::ArrayAllocate (double(*func)(double, double, double), const Pds::Matrix &A, const Pds::Matrix &B, const Pds::Matrix &C)
	crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,B,C). Los tamaño de A, B y C son similares. Más...

static double **	Pds::Matrix::ArrayAllocate (double(*func)(double, double, double, double), const Pds::Matrix &A, const Pds::Matrix &B, const Pds::Matrix &C, double var)
	crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,B,C,var). Los tamaño de A, B y C son similares. Más...

static double **	Pds::Matrix::ArrayAllocate (double(*func)(double, double, double, double), const Pds::Matrix &A, const Pds::Matrix &B, const Pds::Matrix &C, const Pds::Matrix &D)
	crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,B,C,D). Los tamaño de A, B, C y D son similares. Más...

Operadores no miembros
Descripcion de algunos operadores habilitados a trabajar con Pds::Matrix.
std::ostream &	operator<< (std::ostream &out, const Pds::Matrix &mat)
	Retorna el contenido de la matriz por la salida estándar. Más...

Pds::Matrix	operator+ (double b, const Pds::Matrix &A)
	Suma b con (A), el resultado es cargado en C. Este operador es similar al método Add() Más...

Pds::Matrix	operator- (double b, const Pds::Matrix &A)
	Resta b con (A), el resultado es cargado en C. Este operador es similar al método Add() Más...

Pds::Matrix	operator* (double b, const Pds::Matrix &A)
	Multiplica b con (A), el resultado es cargado en C. Este operador es similar al método Mul() Más...

Pds::Matrix	operator/ (double b, const Pds::Matrix &A)
	Divide b con (A), elemento a elemento y el resultado es cargado en C. Este operador es similar al método DivSelf() Más...

Descripción detallada

Clase que implementa una matriz de valores reales.

#include <Pds/Matrix>

Estas funciones trabajan con una matriz de la forma.

$\mathbf{A}=\left(\begin{matrix} a_{00} & a_{01} & \cdots & a_{0(Ncol-1)}\\ a_{10} & a_{11} & \cdots & a_{1(Ncol-1)}\\ \vdots & \vdots & \vdots & \vdots \\ a_{(Nlin-2)0} & a_{(Nlin-2)1} & \cdots & a_{(Nlin-2)(Ncol-1)}\\ a_{(Nlin-1)0} & a_{(Nlin-1)1} & \cdots & a_{(Nlin-1)(Ncol-1)}\\ \end{matrix}\right)$

$A\equiv [a_{i,j}]$

Nlin es el número de lineas y Ncol es el número de columnas.

Información adicional puede ser encontrada en [5]

Documentación de los 'typedefs'

◆ SampleBlock

typedef std::vector<Pds::Matrix> Pds::SampleBlock

Definición de un tipo de dato Pds::SampleBlock.

Definición en la línea 8147 del archivo Matrix.hpp.

◆ BatchBlock

typedef std::vector<std::vector<Pds::Matrix> > Pds::BatchBlock

Definición de un tipo de dato Pds::BatchBlock.

Definición en la línea 8153 del archivo Matrix.hpp.

Documentación de las funciones

◆ Matrix() [1/23]

Pds::Matrix::Matrix ( void )

Crea un objeto de tipo Pds::Matrix vacio.

$\mathbf{A}\equiv []$

Para crear una matriz vacia:

Pds::Matrix A;
 
if(A.IsEmpty()) std::cout<<"Yes,always\n";

◆ Matrix() [2/23]

Pds::Matrix::Matrix ( unsigned int N )

Crea un objeto de tipo Pds::Matrix de N lineas y N columnas, con elementos inicializados con cero.

$\mathbf{A}=\left(\begin{matrix} 0 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0\\ \end{matrix}\right)$

$A_{N,N}\equiv [0]$

Para crear una matriz A de 4 filas y 4 columnas:

Pds::Matrix A(4);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in] N El número de lineas y columnas de la matriz.

◆ Matrix() [3/23]

Pds::Matrix::Matrix ( const Pds::Size & S )

Crea un objeto de tipo Pds::Matrix con elementos inicializados con cero.

$\mathbf{A}=\left(\begin{matrix} 0 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0\\ \end{matrix}\right)$

$A\equiv [0]$

Para crear una matriz A de 4 filas y 3 columnas:

Pds::Matrix B(4,3);
Pds::Matrix A(B.Size);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in] S El tamaño de la matriz.

◆ Matrix() [4/23]

Pds::Matrix::Matrix	(	const Pds::Size &	S,
		double	val
	)

Crea un objeto de tipo Pds::Matrix con elementos inicializados con val.

$\mathbf{A}=\left(\begin{matrix} val & val & \cdots & val\\ val & val & \cdots & val\\ \vdots & \vdots & \vdots & \vdots \\ val & val & \cdots & val\\ val & val & \cdots & val\\ \end{matrix}\right)$

$A\equiv [0]$

Para crear una matriz A de 4 filas y 3 columnas:

Pds::Matrix B(4,3);
Pds::Matrix A(B.Size,1);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in]	S	El tamaño de la matriz.
[in]	val	El valor de los elementos de la matriz.

◆ Matrix() [5/23]

Pds::Matrix::Matrix ( const Pds::Matrix & B )

Crea un objeto de tipo Pds::Matrix copiando datos desde otra matriz. Este es un Copy assignment constructor.

$B\equiv [b_{i,j}]$

$\mathbf{A} \leftarrow \mathbf{B}$

Para crear una matriz A con copia de datos de una matriz B:

Pds::Matrix B(4,3,-1.0);
Pds::Matrix A(B);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in] B Matriz a copiar.

◆ Matrix() [6/23]

template<class Datum >

Pds::Matrix::Matrix ( const Pds::Array< Datum > & B )

Crea un objeto de tipo Pds::Matrix copiando datos desde un arreglo.

Type en Matrix()
Datum	Descripción
double	Variable real
int	Entero con signo
char	caracter (8bits)

$B\equiv [b_{i,j}]$

$\mathbf{A} \leftarrow \mathbf{B}$

Parámetros

[in] B Array a copiar.

◆ Matrix() [7/23]

Pds::Matrix::Matrix ( const char * str )

Crea un objeto de tipo Pds::Matrix copiando datos desde una cadena.

Para crear una matriz A con los datos de una cadena:

Pds::Matrix A="1 2 3\n4 5 6\n";
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in] str Cadena a leer.

◆ Matrix() [8/23]

Pds::Matrix::Matrix ( const std::string & str )

Crea un objeto de tipo Pds::Matrix copiando datos desde una std::string.

Para crear una matriz A con los datos de una cadena:

std::string str=="1 2 3\n4 5 6\n";
Pds::Matrix A(str);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in] str Cadena a leer.

◆ Matrix() [9/23]

Pds::Matrix::Matrix	(	unsigned int	Nlin,
		unsigned int	Ncol
	)

Crea un objeto de tipo Pds::Matrix con elementos inicializados con cero.

$\mathbf{A}=\left(\begin{matrix} 0 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0\\ \end{matrix}\right)$

$A\equiv [0]$

Para crear una matriz A de 4 filas y 3 columnas:

Pds::Matrix A(4,3);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in]	Nlin	El número de lineas de la matriz.
[in]	Ncol	El número de columnas de la matriz.

◆ Matrix() [10/23]

Pds::Matrix::Matrix	(	unsigned int	Nlin,
		unsigned int	Ncol,
		double	val
	)

Crea un objeto de tipo Pds::Matrix con elementos inicializados con val.

$\mathbf{A}=\left(\begin{matrix} val & val & \cdots & val\\ val & val & \cdots & val\\ \vdots & \vdots & \vdots & \vdots \\ val & val & \cdots & val\\ val & val & \cdots & val\\ \end{matrix}\right)$

$A\equiv [val]$

Para crear una matriz A de 4 filas y 3 columnas inicializado con -1:

Pds::Matrix A(4,3,-1.0);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in]	Nlin	El número de lineas de la matriz.
[in]	Ncol	El número de columnas de la matriz.
[in]	val	El valor a usar.

◆ Matrix() [11/23]

Pds::Matrix::Matrix	(	double(*)(double)	func,
		const Pds::Matrix &	B
	)

Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz.

$B\equiv [b_{i,j}]$

$\mathbf{A} \leftarrow func(\mathbf{B})$

Para crear una matriz A , copia de sin(B):

Pds::Matrix B(4,3,1.0);
Pds::Matrix A(sin,B);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double).
[in]	B	Matriz a evaluar para copiar los resultados.

◆ Matrix() [12/23]

Pds::Matrix::Matrix	(	double(*)(double, double)	func,
		const Pds::Matrix &	B,
		double	var
	)

Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz.

$B\equiv [b_{i,j}]$

$\mathbf{A} \leftarrow func(\mathbf{B},var)$

Para crear una matriz A , copia de pow(B,3):

Pds::Matrix B(4,3,2.0);
Pds::Matrix A(pow,B,3);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double,double).
[in]	B	Matriz a evaluar para copiar los resultados.
[in]	var	Segunda variable de la función.

◆ Matrix() [13/23]

Pds::Matrix::Matrix	(	double(*)(double, double)	func,
		const Pds::Matrix &	B,
		const Pds::Matrix &	C
	)

Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz.

$B\equiv [b_{ij}], \qquad C\equiv [c_{ij}]$

$\mathbf{A} \leftarrow func(\mathbf{B},\mathbf{C})$

$\mathbf{a}_{ij} \leftarrow func(\mathbf{b}_{ij},\mathbf{c}_{ij})$

Para crear una matriz A , copia de pow(B,C):

Pds::Matrix B(2,3,2.0);
Pds::Matrix C(2,3,3.0);
Pds::Matrix A(pow,B,C);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in]	func	Función a aplicar elemento a elemento en las matrices, esta debe tener a forma double func(double,double).
[in]	B	Matriz a evaluar para copiar los resultados.
[in]	C	Matriz a evaluar para copiar los resultados.

◆ Matrix() [14/23]

Pds::Matrix::Matrix	(	double(*)(double, double, double)	func,
		const Pds::Matrix &	B,
		const Pds::Matrix &	C,
		double	var
	)

Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz.

$B\equiv [b_{ij}], \qquad C\equiv [c_{ij}]$

$\mathbf{A} \leftarrow func(\mathbf{B},\mathbf{C},var)$

$\mathbf{a}_{ij} \leftarrow func(\mathbf{b}_{ij},\mathbf{c}_{ij},var)$

Para crear una matriz A , copia de func(B,C,var):

Pds::Matrix B(2,3,2.0);
Pds::Matrix C(2,3,3.0);
double var=2;
Pds::Matrix A(func,B,C,var);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in]	func	Función a aplicar elemento a elemento en las matrices, esta debe tener a forma double func(double,double,double).
[in]	B	Matriz a evaluar para copiar los resultados.
[in]	C	Matriz a evaluar para copiar los resultados.
[in]	var	Tercera variable de la función.

◆ Matrix() [15/23]

Pds::Matrix::Matrix	(	double(*)(double, double, double)	func,
		const Pds::Matrix &	X,
		const Pds::Matrix &	Y,
		const Pds::Matrix &	Z
	)

Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz.

$X\equiv [x_{ij}], \qquad Y\equiv [y_{ij}], \qquad Z\equiv [z_{ij}]$

$\mathbf{A} \leftarrow func(\mathbf{X},\mathbf{Y},\mathbf{Z})$

$\mathbf{a}_{ij} \leftarrow func(\mathbf{x}_{ij},\mathbf{y}_{ij},\mathbf{z}_{ij})$

Para crear una matriz A , copia de func(X,Y,Z):

Pds::Matrix X(2,3,2.0);
Pds::Matrix Y(2,3,3.0);
Pds::Matrix Z(2,3,1.0);
Pds::Matrix A(func,X,Y,Z);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in]	func	Función a aplicar elemento a elemento en las matrices, esta debe tener a forma double func(double,double,double).
[in]	X	Matriz a evaluar para copiar los resultados.
[in]	Y	Matriz a evaluar para copiar los resultados.
[in]	Z	Matriz a evaluar para copiar los resultados.

◆ Matrix() [16/23]

Pds::Matrix::Matrix	(	double(*)(double, double, double, double)	func,
		const Pds::Matrix &	X,
		const Pds::Matrix &	Y,
		const Pds::Matrix &	Z,
		double	var
	)

Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz.

$X\equiv [x_{ij}], \qquad Y\equiv [y_{ij}], \qquad Z\equiv [z_{ij}]$

$\mathbf{A} \leftarrow func(\mathbf{X},\mathbf{Y},\mathbf{Z},var)$

$\mathbf{a}_{ij} \leftarrow func(\mathbf{x}_{ij},\mathbf{y}_{ij},\mathbf{z}_{ij},var)$

Para crear una matriz A , copia de func(X,Y,Z,var):

Pds::Matrix X(2,3,2.0);
Pds::Matrix Y(2,3,3.0);
Pds::Matrix Z(2,3,1.0);
double var=2;
Pds::Matrix A(func,X,Y,Z,var);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in]	func	Función a aplicar elemento a elemento en las matrices, esta debe tener a forma double func(double,double,double,double).
[in]	X	Matriz a evaluar para copiar los resultados.
[in]	Y	Matriz a evaluar para copiar los resultados.
[in]	Z	Matriz a evaluar para copiar los resultados.
[in]	var	Cuarto valor a evaluar.

◆ Matrix() [17/23]

Pds::Matrix::Matrix	(	double(*)(double, double, double, double)	func,
		const Pds::Matrix &	X,
		const Pds::Matrix &	Y,
		const Pds::Matrix &	Z,
		const Pds::Matrix &	W
	)

Crea un objeto de tipo Pds::Matrix, evaluando mediante una función, los datos de otra matriz.

$X\equiv [x_{ij}], \qquad Y\equiv [y_{ij}], \qquad Z\equiv [z_{ij}], \qquad W\equiv [w_{ij}]$

$\mathbf{A} \leftarrow func(\mathbf{X},\mathbf{Y},\mathbf{Z},\mathbf{W})$

$\mathbf{a}_{ij} \leftarrow func(\mathbf{x}_{ij},\mathbf{y}_{ij},\mathbf{z}_{ij},\mathbf{w}_{ij})$

Para crear una matriz A , copia de func(X,Y,Z,W):

Pds::Matrix X(2,3,2.0);
Pds::Matrix Y(2,3,3.0);
Pds::Matrix Z(2,3,1.0);
Pds::Matrix W(2,3,1.0);
Pds::Matrix A(func,X,Y,Z,W);
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in]	func	Función a aplicar elemento a elemento en las matrices, esta debe tener a forma double func(double,double,double,double).
[in]	X	Matriz a evaluar para copiar los resultados.
[in]	Y	Matriz a evaluar para copiar los resultados.
[in]	Z	Matriz a evaluar para copiar los resultados.
[in]	W	Matriz a evaluar para copiar los resultados.

◆ Matrix() [18/23]

Pds::Matrix::Matrix	(	Pds::Ra::FormatType	Type,
		std::string	filepath
	)

Crea un objeto de tipo Pds::Matrix copiando datos desde un archivo.

Pds::Matrix A(Pds::Ra::TextFormat,"textfile.txt");
 
if(A.IsEmpty()) std::cout<<"Yes,possible memory allocation problem\n";
else            std::cout<<"No,all fine\n";

Parámetros

[in]

Type

Tipo de archivo de fuente de datos. Los tipos aceptados son:

Pds::Ra::TextFormat

Lee en formato de texto.

[in] filepath Path del archivo cargado.

◆ Matrix() [19/23]

Pds::Matrix::Matrix ( const std::vector< Pds::Point2D > & P )

Crea una matriz de dos columnas, en la primera columna estan los elementos X y en la segunda columna los elelentos Y.

$\mathbf{A} \leftarrow \begin{bmatrix} P[0].X & P[0].Y\\ P[1].X & P[1].Y\\ \vdots&\vdots\\ P[n].X & P[n].Y\\ \vdots&\vdots\\ P[N-1].X & P[N-1].Y\\ \end{bmatrix}$

Parámetros

[in] P Vector de Pds::Point2D a copiar.

◆ Matrix() [20/23]

Pds::Matrix::Matrix ( const std::vector< Pds::Position > & P )

Crea una matriz de dos columnas, en la primera columna estan los elementos Lin y en la segunda columna los elelentos Col.

$\mathbf{A} \leftarrow \begin{bmatrix} P[0].Lin & P[0].Col\\ P[1].Lin & P[1].Col\\ \vdots&\vdots\\ P[n].Lin & P[n].Col\\ \vdots&\vdots\\ P[N-1].Lin & P[N-1].Col\\ \end{bmatrix}$

Parámetros

[in] P Vector de Pds::Position a copiar.

◆ Matrix() [21/23]

template<class Datum >

Pds::Matrix::Matrix ( const std::vector< Datum > & P )

Crea una matriz de una columna, en esa columna estan los elementos del vector.

Type en Matrix()
Datum	Descripción
double	Variable real
int	Entero con signo
unsigned int	Entero sin signo
bool	Booleano

Por exemplo

$\mathbf{A} \leftarrow \begin{bmatrix} P[0]\\ P[1]\\ \vdots&\vdots\\ P[n]\\ \vdots\\ P[N-1]\\ \end{bmatrix}$

Atención: Datum está habilitado para {bool,int,unsigned int,double}

Parámetros

[in] P Vector de datos a copiar.

◆ Matrix() [22/23]

template<class Datum >

Pds::Matrix::Matrix	(	unsigned int	Nlin,
		unsigned int	Ncol,
		const std::vector< Datum > &	P
	)

Crea una matriz Nlin lineas y Ncol columnas usando los elementos del vector.

Type en Matrix()
Datum	Descripción
double	Variable real
int	Entero con signo
unsigned int	Entero sin signo
bool	Booleano

Por exemplo

$\mathbf{A} \leftarrow \begin{bmatrix} P[0]&P[Nlin]&\hdots&P[(Ncol-1)Nlin]\\ P[1]&P[Nlin+1]&\hdots&P[(Ncol-1)Nlin+1]\\ \vdots&\vdots&\hdots&\vdots\\ P[n]&P[Nlin+n]&\hdots&P[(Ncol-1)Nlin+n]\\ \vdots&\vdots&\hdots&\vdots\\ P[Nlin-1]&P[2*Nlin-1]&\hdots&P[Ncol*Nlin-1]\\ \end{bmatrix}$

Atención: Si el tamanho de P es menor a Nlin*Ncol se completa con zeros, si es mayor se descartan los sobrantes.

Parámetros

[in]	Nlin	Número de lineas.
[in]	Ncol	Número de columnas.
[in]	P	Vector de datos a copiar, puede ser incluso uno vacio.

◆ Matrix() [23/23]

template<class Datum >

Pds::Matrix::Matrix ( const std::initializer_list< Datum > & list )

Crea una matriz de una columna, en esa columna estan los elementos del vector.

Type en Matrix()
Datum	Descripción
double	Variable real
int	Entero con signo
bool	Booleano

Por exemplo

$\mathbf{A} \leftarrow \begin{bmatrix} list[0]\\ list[1]\\ \vdots&\vdots\\ list[n]\\ \vdots\\ list[N-1]\\ \end{bmatrix}$

Atención: Datum está habilitado para {bool,int,double}

Parámetros

[in] list Lista de datos a copiar.

◆ IsEmpty()

bool Pds::Matrix::IsEmpty ( void ) const

Verifica si la matriz es nula es decir con lineas o columnas cero o arreglo NULL.

Una matriz $\mathbf{A}$ está vacía si $\mathbf{A}=[]$ .

Devuelve: Retorna true si es nula e false si no.

Ejemplos: example_matrix_operaterows.cpp y example_regression_fitting.cpp.

◆ IsNotEmpty()

bool Pds::Matrix::IsNotEmpty ( void ) const

Verifica si la matriz NO es nula, es decir con lineas y columnas diferentes cero y arreglo diferente de NULL.

Una matriz $\mathbf{A}$ está vacía si $\mathbf{A}=[]$ .

Devuelve: Retorna true si NO es nula e false si lo es.

Ejemplos: example_matrix_save_load.cpp.

◆ IsSimilarTo()

bool Pds::Matrix::IsSimilarTo ( const Pds::Matrix & B ) const

Verifica si las matrices son similares en tamaño.

Una matriz $A_{M,N}$ es similar a $B_{P,Q}$ si y .

Parámetros

[in] B Matriz en consulta.

Devuelve: Retorna true si son similares y false si no.

◆ IsNotSimilarTo()

bool Pds::Matrix::IsNotSimilarTo ( const Pds::Matrix & B ) const

Verifica si las matrices son similares en tamaño.

Una matriz $A_{M,N}$ es similar a $B_{P,Q}$ si y .

Parámetros

[in] B Matriz en consulta.

Devuelve: Retorna false si son similares y true si no.

◆ IsMulBy()

bool Pds::Matrix::IsMulBy ( const Pds::Matrix & B ) const

Verifica si las matrices son multiplicables.

Una matriz $A_{M,N}$ es multiplicable por $B_{P,Q}$ si y ambas son no vacías.

Parámetros

[in] B Matriz en consulta.

Devuelve: Retorna true si son multiplicables y false si no.

◆ IsNotMulBy()

bool Pds::Matrix::IsNotMulBy ( const Pds::Matrix & B ) const

Verifica si las matrices son multiplicables.

Una matriz $A_{M,N}$ es multiplicable por $B_{P,Q}$ si y ambas son no vacías.

Parámetros

[in] B Matriz en consulta.

Devuelve: Retorna false si son multiplicables y true si no.

◆ IsInRange()

bool Pds::Matrix::IsInRange	(	unsigned int	lin,
		unsigned int	col
	)		const

Verifica si la posición pertenece a la matriz.

Dada una matriz $A_{M,N}$ ; la posición está en rango de $\mathbf{A}$ si cualquier valor entero de $0\leq lin \leq M-1$ y cualquier valor entero de $0\leq col \leq N-1$ .

Parámetros

[in]	lin	Linea en consulta.
[in]	col	columna en consulta.

Devuelve: Retorna true si pertenece y false si no.

◆ IsNotInRange()

bool Pds::Matrix::IsNotInRange	(	unsigned int	lin,
		unsigned int	col
	)		const

Verifica si la posición NO pertenece a la matriz.

Dada una matriz $A_{M,N}$ ; la posición está en rango de $\mathbf{A}$ si cualquier valor entero de $0\leq lin \leq M-1$ y cualquier valor entero de $0\leq col \leq N-1$ .

Parámetros

[in]	lin	Linea en consulta.
[in]	col	columna en consulta.

Devuelve: Retorna false si pertenece y true si no.

◆ IsInSizeRange()

bool Pds::Matrix::IsInSizeRange	(	double	lin,
		double	col
	)		const

Verifica si la posición (lin,col) pertenece al rango de la matriz.

Dada una matriz $A_{M,N}$ ; la posición está en rango de $\mathbf{A}$ si cualquier valor real de $0\leq lin \leq M-1$ y cualquier valor real de $0\leq col \leq N-1$ .

Parámetros

[in]	lin	Linea en consulta.
[in]	col	columna en consulta.

Devuelve: Retorna true si pertenece y false si no.

◆ IsRowMatrix()

bool Pds::Matrix::IsRowMatrix ( void ) const

Verifica si la matriz tiene solo una linea.

Devuelve: Retorna true si la matriz tiene solo una linea o false si no. Si la matriz está vacia se retorna false.

◆ IsColMatrix()

bool Pds::Matrix::IsColMatrix ( void ) const

Verifica si la matriz tiene solo una columna.

Devuelve: Retorna true si la matriz tiene solo una columna o false si no. Si la matriz está vacia se retorna false.

◆ IsZero()

bool Pds::Matrix::IsZero ( void ) const

Verifica si la matriz está llena de zeros.

$true \overleftarrow{IsZero} \left(\begin{matrix} 0 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0\\ \end{matrix}\right)$

Devuelve: Retorna true si la matriz está llena de zeros o false si no. Si la matriz está vacia se retorna false.

◆ IsLeq() [1/2]

bool Pds::Matrix::IsLeq ( double val ) const

Verifica si cada elemento de la matriz es menor a el valor val.

$\mathbf{A}~<=~val$

Parámetros

[in] val El valor a comparar.

Devuelve: Retorna true si todos los elementos son menores que val y false si no.

◆ IsLeq() [2/2]

bool Pds::Matrix::IsLeq ( const Pds::Matrix & B ) const

Verifica si cada elemento de la matriz es menor igual a cada elemento de la matriz B.

$\mathbf{A}~<=~\mathbf{B}$

Parámetros

[in] B Matriz a comparar.

Devuelve: Retorna true si todos los elementos son menores y false si no.

◆ IsGeq() [1/2]

bool Pds::Matrix::IsGeq ( double val ) const

Verifica si cada elemento de la matriz es mayor a el valor val.

$\mathbf{A}~>=~val$

Parámetros

[in] val El valor a comparar.

Devuelve: Retorna true si todos los elementos son mayores que val y false si no.

◆ IsGeq() [2/2]

bool Pds::Matrix::IsGeq ( const Pds::Matrix & B ) const

Verifica si cada elemento de la matriz es mayor igual a cada elemento de la matriz B.

$\mathbf{A}~>=~\mathbf{B}$

Parámetros

[in] B Matriz a comparar.

Devuelve: Retorna true si todos los elementos son mayores y false si no.

◆ IsEqualTo() [1/2]

bool Pds::Matrix::IsEqualTo ( double val ) const

Verifica si cada elemento de la matriz es igual a el valor val.

$\mathbf{A}~==~val$

Parámetros

[in] val El valor a comparar.

Devuelve: Retorna true si todos los elementos son iguale a val y false si no.

◆ IsEqualTo() [2/2]

bool Pds::Matrix::IsEqualTo ( const Pds::Matrix & B ) const

Verifica si cada elemento de la matriz es igual a cada elemento de la matriz B.

$\mathbf{A}~==~\mathbf{B}$

Parámetros

[in] B Matriz a comparar.

Devuelve: Retorna true si todos los elementos son iguales y false si no.

◆ HasLeq()

bool Pds::Matrix::HasLeq ( double val ) const

Verifica si existe al menos un elemento de la matriz menor o igual a el valor val.

$\mathbf{A}~<=~val?$

Parámetros

[in] val El valor a comparar.

Devuelve: Retorna true si existe al menos un elemento menor o igual que val y false si no.

◆ HasGeq()

bool Pds::Matrix::HasGeq ( double val ) const

Verifica si existe al menos un elemento de la matriz mayor o igual a el valor val.

$\mathbf{A}~>=~val?$

Parámetros

[in] val El valor a comparar.

Devuelve: Retorna true si existe al menos un elemento mayor o igual que val y false si no.

◆ HasInf()

bool Pds::Matrix::HasInf ( void ) const

Verifica si la matriz tiene algun valor infinito.

Los valores infinitos pueden producirse con $+\frac{1}{0},-\frac{1}{0} y \frac{1}{0}$ .

$true\qquad \overleftarrow{HasInf()}\qquad \left(\begin{matrix} 1 & NaN & NaN\\ 0 & 2 & -\infty\\ \infty & 0 & 0\\ 3 & -\infty & NaN\\ \end{matrix}\right)$

Devuelve: Retorna true si tiene algun elemento infinito y false si no lo tiene.

◆ HasNan()

bool Pds::Matrix::HasNan ( void ) const

Verifica si la matriz tiene algun valor NAN (Not A Number).

Los valores NAN pueden producirse con $\frac{0}{0}$ .

$true\qquad \overleftarrow{EqualToNan()}\qquad \left(\begin{matrix} 1 & NaN & NaN\\ 0 & 2 & -\infty\\ \infty & 0 & 0\\ 3 & -\infty & NaN\\ \end{matrix}\right)$

Devuelve: Retorna true si tiene NAN y false si no lo tiene.

◆ HasNotFinite()

bool Pds::Matrix::HasNotFinite ( void ) const

Verifica si la matriz tiene elementos no finitos (+inf, -inf y NAN).

$true\qquad \overleftarrow{EqualToFinite()}\qquad \left(\begin{matrix} 1 & NaN & NaN\\ 0 & 2 & -\infty\\ \infty & 0 & 0\\ 3 & -\infty & NaN\\ \end{matrix}\right)$

Devuelve: Retorna true si tiene un valor no finito y false si no lo tiene.

◆ FillRandC()

bool Pds::Matrix::FillRandC ( double p1 )

Inicializa la matriz con números aleatórios unos y ceros, la probabilidad de 1 es p1.

Atención: La función usa internamente la función rand(), si se desea esta puede ser aleatoriamente inicializada usando la funcíón Pds::Ra::Randomize(), de lo contrario los números pseudo aleatórios siempre seguirán la misma secuencia.

Parámetros

[in] p1 Probabilidad de acontecer un 1.

Devuelve: Retorna true si todo fue bien o false si no.

Ejemplos: example_matrix_assignment_bin.cpp, example_matrix_json.cpp, example_matrix_operators_binary.cpp, example_matrix_operators_binary2.cpp, example_matrixmath.cpp y example_vector_json.cpp.

◆ FillRandN() [1/2]

bool Pds::Matrix::FillRandN ( void )

Inicializa la matriz con números aleatórios, distribuidos usando una distribución Gaussiana normalizada con media 0 y desvío padrón 1.0.

Atención: La función usa internamente la función rand(), si se desea esta puede ser aleatoriamente inicializada usando la funcíón Pds::Ra::Randomize(), de lo contrario los números pseudo aleatórios siempre seguirán la misma secuencia.

$f_{X}(x)=\frac {1}{\sqrt {2\pi }} e^{-{\frac {1}{2}}x^{2}},~~x \in R$

$\mathbf{A}\equiv [a_{i,j}]_{M,N}$

$a_{i,j}\leftarrow X_{l} \in X$

Devuelve: Retorna true si todo fue bien o false si no.

Ejemplos: example_matrix_algebra_cholesky.cpp, example_matrixmath.cpp y example_optadam_create.cpp.

◆ FillRandN() [2/2]

bool Pds::Matrix::FillRandN	(	double	U,
		double	Sigma
	)

Inicializa la matriz con números aleatórios, distribuidos usando una distribución Gaussiana con media U y desvío padrón Sigma.

Atención: La función usa internamente la función rand(), si se desea esta puede ser aleatoriamente inicializada usando la funcíón Pds::Ra::Randomize(), de lo contrario los números pseudo aleatórios siempre seguirán la misma secuencia.

$f_{X}(x)=\frac {1}{\sigma \sqrt {2\pi }} e^{-{\frac {(x-\mu)^{2}}{2\sigma^2}}},~~x \in R$

$\mathbf{A}\equiv [a_{i,j}]_{M,N}$

$a_{i,j}\leftarrow X_{l} \in X$

Parámetros

[in]	U	Valor da media $\mu$ .
[in]	Sigma	Valor do desvio padron $\sigma$ .

Devuelve: Retorna true si todo fue bien o false si no.

◆ FillRandU() [1/3]

bool Pds::Matrix::FillRandU ( void )

Inicializa la matriz con números aleatórios, distribuidos uniformemente, desde 0 a 1.0, incluyendo 0 y excluyendo 1.0.

Atención: La función usa internamente la función rand(), si se desea esta puede ser aleatoriamente inicializada usando la funcíón Pds::Ra::Randomize(), de lo contrario los números pseudo aleatórios siempre seguirán la misma secuencia.

$f_{X}(x)= 1,~~0\leq x<1, x \in R$

$\mathbf{A}\equiv [a_{i,j}]_{M,N}$

$a_{i,j}\leftarrow X_{l} \in X$

Devuelve: Retorna true si todo fue bien o false si no.

Ejemplos: example_matrix_algebra3.cpp, example_matrix_fill.cpp, example_matrix_save_load.cpp, example_matrixmath.cpp, example_octave_show.cpp, example_triangle_evalsamples.cpp y example_vector_sorting.cpp.

◆ FillRandU() [2/3]

bool Pds::Matrix::FillRandU	(	int	a,
		int	b
	)

Inicializa la matriz con números aleatórios, distribuidos uniformemente, desde a a b, incluyendo a y b.

Atención: La función usa internamente la función rand(), si se desea esta puede ser aleatoriamente inicializada usando la funcíón Pds::Ra::Randomize(), de lo contrario los números pseudo aleatórios siempre seguirán la misma secuencia.

$f_{X}(x)= 1,~~min(a,b)\leq x\leq max(a,b), x \in R$

$\mathbf{A}\equiv [a_{i,j}]_{M,N}$

$a_{i,j}\leftarrow X_{l} \in X$

Parámetros

[in]	a	Valor mínimo posible.
[in]	b	Valor máximo posible.

Devuelve: Retorna true si todo fue bien o false si no.

◆ FillRandU() [3/3]

bool Pds::Matrix::FillRandU	(	double	a,
		double	b
	)

Inicializa la matriz con números aleatórios, distribuidos uniformemente, desde a a b, incluyendo a y b.

Atención: La función usa internamente la función rand(), si se desea esta puede ser aleatoriamente inicializada usando la funcíón Pds::Ra::Randomize(), de lo contrario los números pseudo aleatórios siempre seguirán la misma secuencia.

$f_{X}(x)= 1,~~min(a,b)\leq x\leq max(a,b), x \in R$

$\mathbf{A}\equiv [a_{i,j}]_{M,N}$

$a_{i,j}\leftarrow X_{l} \in X$

Parámetros

[in]	a	Valor mínimo posible.
[in]	b	Valor máximo posible.

Devuelve: Retorna true si todo fue bien o false si no.

◆ FillId()

bool Pds::Matrix::FillId ( void )

Inicializa la matriz con el valor de la posición de cada elemento.

En el caso de una matriz A de 4 lineas y 3 columnas:

$\mathbf{A} \leftarrow \left(\begin{matrix} 0 & 4 & 8\\ 1 & 5 & 9\\ 2 & 6 & 10\\ 3 & 7 & 11\\ \end{matrix}\right)$

Devuelve: Retorna true si todo fue bien o false si no.

Ejemplos: example_array_create.cpp, example_array_dsp.cpp, example_matrix_algebra3.cpp, example_matrix_algebra4.cpp, example_matrix_algebra_cholesky.cpp, example_matrix_export.cpp, example_matrix_export_json.cpp, example_matrix_fill.cpp, example_matrix_getset.cpp, example_matrix_operators_binary2.cpp, example_matrix_sampleblock.cpp, example_matrix_static_matrix.cpp, example_ra_indices.cpp, example_vector_export_json.cpp, example_vector_operator_unit.cpp y example_vector_sorting.cpp.

◆ FillBcd()

bool Pds::Matrix::FillBcd ( unsigned int n )

Escribe un número en digital codificado en binário (BCD), escribe primero en una columna entera y luego pasa a la siguiente.

Parámetros

[in] n Número a escribir en BCD.

Devuelve: Retorna true si todo fue bien o false si no.

Ejemplos: example_matrix_fill.cpp.

◆ Fill() [1/3]

bool Pds::Matrix::Fill ( Pds::AbstractRV & RV )

Inicializa la matriz con un valor aleatório.

Parámetros

[in] RV La rv.

Devuelve: Retorna true si todo fue bien o false si no.

Ejemplos: example_matrix_fill.cpp, example_matrix_fill_rv.cpp, example_matrix_getset_extras.cpp, example_matrix_operators_binary.cpp, example_matrix_operators_binary2.cpp, example_matrixmath.cpp y example_ra_indices.cpp.

◆ Fill() [2/3]

bool Pds::Matrix::Fill ( double val )

Inicializa la matriz con un valor constante.

$\mathbf{A} \leftarrow \left(\begin{matrix} val & val & \cdots & val\\ val & val & \cdots & val\\ \vdots & \vdots & \vdots & \vdots \\ val & val & \cdots & val\\ val & val & \cdots & val\\ \end{matrix}\right)$

Parámetros

[in] val El valor a ser usado.

Devuelve: Retorna true si todo fue bien o false si no.

◆ Fill() [3/3]

template<class Datum >

bool Pds::Matrix::Fill ( const std::vector< Datum > & P )

Inicializa la matriz con un valor constante.

Type en Fill()
Datum	Descripción
double	Variable real
int	Entero con signo
bool	Booleano

Por exemplo

$\mathbf{A} \leftarrow \begin{bmatrix} P[0]&P[Nlin]&\hdots&P[(Ncol-1)Nlin]\\ P[1]&P[Nlin+1]&\hdots&P[(Ncol-1)Nlin+1]\\ \vdots&\vdots&\hdots&\vdots\\ P[n]&P[Nlin+n]&\hdots&P[(Ncol-1)Nlin+n]\\ \vdots&\vdots&\hdots&\vdots\\ P[Nlin-1]&P[2*Nlin-1]&\hdots&P[Ncol*Nlin-1]\\ \end{bmatrix}$

Atención: Si el tamanho de P es menor a Nlin*Ncol se completa con zeros, si es mayor se descartan los sobrantes.

Parámetros

[in] P El vector a ser usado.

Devuelve: Retorna true si todo fue bien o false si no.

◆ FillLinSpace()

bool Pds::Matrix::FillLinSpace	(	double	a,
		double	b
	)

Inicializa la matriz con un espacio linear entre begin y end. Se inicializa primero una columna ante de pasar ala siguiente.

En el caso de una matriz A de Nlin=4 lineas y Ncol=3 columnas:

$\alpha= \frac{b-a}{Nlin~Ncol- 1}$

$\mathbf{A} \leftarrow \left(\begin{matrix} a & 4\alpha+a & 8\alpha+a\\ \alpha+a & 5\alpha+a & 9\alpha+a\\ 2\alpha+a & 6\alpha+a & 10\alpha+a\\ 3\alpha+a & 7\alpha+a & 11\alpha+a\\ \end{matrix}\right)$

Parámetros

[in]	a	El valor inicial.
[in]	b	El valor final.

Devuelve: Retorna true si todo fue bien o false si no.

Ejemplos: example_matrix_fill.cpp.

◆ Nlin()

unsigned int Pds::Matrix::Nlin ( void ) const

Retorna el número de lineas de la matriz.

Devuelve: Retorna el número de lineas de la matriz.

Ejemplos: example_ellipse_getellipse.cpp, example_line2d_create.cpp y example_vector_dsp.cpp.

◆ Ncol()

unsigned int Pds::Matrix::Ncol ( void ) const

Retorna el número de columnas de la matriz.

Devuelve: Retorna el número de columnas de la matriz.

◆ Nel()

unsigned int Pds::Matrix::Nel ( void ) const

Retorna el número de elementos de la matriz (Nlin x Ncol).

Devuelve: Retorna el número de elementos de la matriz.

Ejemplos: example_binarytreenode.cpp, example_matrix_dsp2.cpp, example_matrix_dsp_hist.cpp y example_regression_fitting.cpp.

◆ Size()

Pds::Size Pds::Matrix::Size ( void ) const

Retorna un objeto de tipo Pds::Size con el número de lineas y columans.

Devuelve: Retorna el tamano de la matriz.

Ejemplos: example_matrix_dsp.cpp, example_matrix_kernel_gabor.cpp, example_matrix_kernel_gaussian.cpp, example_octave_pairwisescatterxy.cpp, example_optadam_create.cpp, example_vector_create.cpp y example_vector_poly.cpp.

◆ LinEnd()

unsigned int Pds::Matrix::LinEnd ( void ) const

Retorna el identificador de la ultima linea de la matriz.

Devuelve: Retorna Nlin-1.

Ejemplos: example_matrix_getset.cpp.

◆ ColEnd()

unsigned int Pds::Matrix::ColEnd ( void ) const

Retorna el identificador de la ultima columna de la matriz.

Devuelve: Retorna Ncol-1.

Ejemplos: example_matrix_getset.cpp.

◆ End()

unsigned int Pds::Matrix::End ( void ) const

Retorna el identificador del ultimo elemento de la matriz.

Devuelve: Retorna ((Nlin x Ncol)-1).

◆ Get() [1/4]

double Pds::Matrix::Get ( unsigned int id ) const

Retorna el valor en la posición del índice id, hace una verificación si la posición existe.

Parámetros

[in] id índice de un elemento de la matriz.

Devuelve: Retorna el valor en la posición (id%Nlin,id/Nlin) o cero si la posición no existe.

Ejemplos: example_matrix_algebra.cpp y example_matrix_getset.cpp.

◆ Get() [2/4]

double Pds::Matrix::Get	(	unsigned int	lin,
		unsigned int	col
	)		const

Retorna el valor en la posición (lin,col), hace una verificación si la posición existe.

Parámetros

[in]	lin	La linea en consulta.
[in]	col	La columna en consulta.

Devuelve: Retorna el valor en la posición (lin,col) o cero si la posición no existe.

◆ Get() [3/4]

Pds::Vector Pds::Matrix::Get ( const std::vector< Pds::Position > & P ) const

Retorna el valor en las posiciones P[n]. Hace una verificación si la posiciones existen.

Parámetros

[in] P Posiciones en consulta.

Devuelve: Retorna un vector con los valores de las posiciones P[n] o cero si la posición no existe.

◆ Get() [4/4]

double Pds::Matrix::Get ( const Pds::Position & P ) const

Retorna el valor en la posición (lin,col), hace una verificación si la posición existe.

Parámetros

[in] P Posicion P=(lin,col) del elemento en consulta.

Devuelve: Retorna el valor en la posición P=(lin,col) o cero si la posición no existe.

◆ GetRaw()

const double & Pds::Matrix::GetRaw	(	unsigned int	lin,
		unsigned int	col
	)		const

inline

Retorna una variable double en la posición (lin,col) de la array.

Atención: NO hace una verificación para evitar leer fuera de la memoria, por lo que dará errores de acceso si pedimos una posición inexistente.

Parámetros

[in]	lin	La linea en consulta.
[in]	col	La columna en consulta.

Devuelve: Retorna una variable double en la posición (lin,col).

Definición en la línea 1305 del archivo Matrix.hpp.

    {
        return this->array[lin][col];
    }

◆ SetRaw()

void Pds::Matrix::SetRaw	(	unsigned int	lin,
		unsigned int	col,
		const double &	val
	)

inline

Establece una variable double en la posición (lin,col) de la array.

Atención: NO hace una verificación para evitar leer fuera de la memoria, por lo que dará errores de acceso si pedimos una posición inexistente.

Parámetros

[in]	lin	La linea en consulta.
[in]	col	La columna en consulta.
[in]	val	valor a escribir.

Definición en la línea 1319 del archivo Matrix.hpp.

    {
        this->array[lin][col]=val;
    }

◆ Set() [1/2]

bool Pds::Matrix::Set	(	unsigned int	id,
		double	val
	)

Escribe el valor en la posición del índice id, hace una verificación si la posición existe.

Parámetros

[in]	val	valor a escribir.
[in]	id	índice de un elemento de la matriz.

Devuelve: Retorna true si consiguió escribir el valor en la posición (id%Nlin,id/Nlin) o false si no.

◆ Set() [2/2]

bool Pds::Matrix::Set	(	unsigned int	lin,
		unsigned int	col,
		double	val
	)

Escribe el valor en la posición (lin,col), hace una verificación si la posición existe.

Parámetros

[in]	val	valor a escribir.
[in]	lin	La linea en consulta.
[in]	col	La columna en consulta.

Devuelve: Retorna true si consiguió escribir el valor en la posicion (lin,col) o false si no.

◆ In() [1/2]

double & Pds::Matrix::In	(	unsigned int	lin,
		unsigned int	col
	)

Retorna una variable double en la posición (lin,col) de la matriz. Hace una verificación para evitar leer o escribir fuera de la memoria, con este fin hace lin=linNlin y col=colNcol.

Parámetros

[in]	lin	La linea en consulta.
[in]	col	La columna en consulta.

Devuelve: Retorna una variable double en la posición (lin,col).

Ejemplos: example_matrix_getset.cpp.

◆ In() [2/2]

double & Pds::Matrix::In ( unsigned int id )

Retorna una variable double en la posición (id) de la matriz. Hace una verificación para evitar leer o escribir fuera de la memoria, con este fin hace id=id%(Nlin*Ncol).

Parámetros

[in] id La posicion en consulta.

Devuelve: Retorna una variable double en la posición (id).

◆ Bilinear()

double Pds::Matrix::Bilinear	(	double	lin,
		double	col
	)		const

Retorna el valor en la posición (lin,col), usando una interpolación bilinear, valores fuera del rango de la matriz retornan cero.

Matrix A

$A(P) \leftarrow (1-\beta)(1-\alpha)A(P_1)+(1-\beta)\alpha A(P_2)+\beta(1-\alpha)A(P_3)+ \beta \alpha A(P_4)$

Parámetros

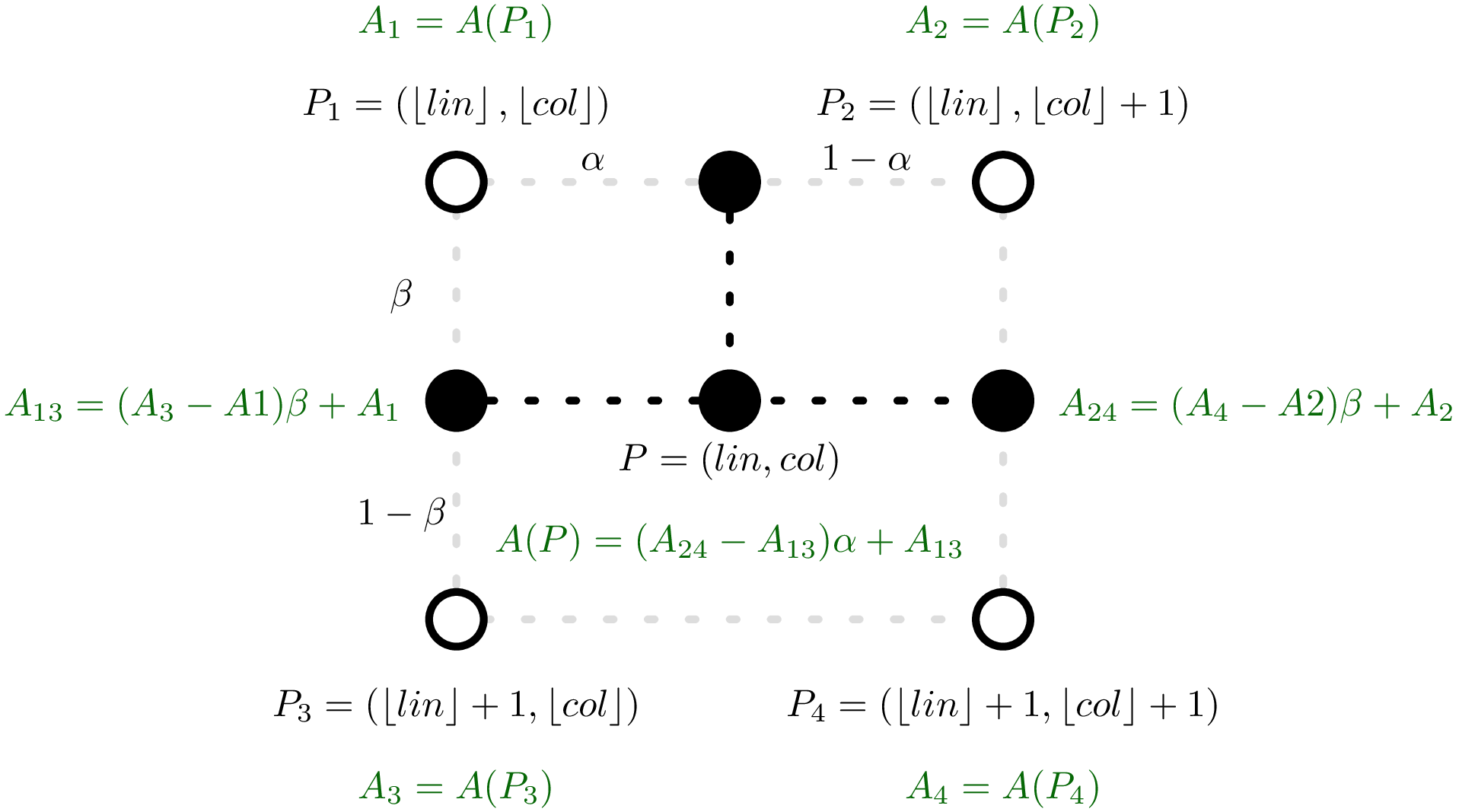
[in]	lin	La linea en consulta.
[in]	col	La columna en consulta.

Devuelve: Retorna el valor en la posición P=(lin,col) o cero si lin<0 o col<0 o lin>(Nlin-1) o col>(Ncol-1).

Ejemplos: example_matrix_getset.cpp.

◆ GetDiagonal()

Pds::Vector Pds::Matrix::GetDiagonal ( void ) const

Retorna un vector columna copia de los valores de la diagonal de la matriz.

Devuelve: Retorna el vector columna en la posición (col) o un vector vacío en caso de error.

Ejemplos: example_matrix_getset_extras.cpp.

◆ SetDiagonal() [1/2]

bool Pds::Matrix::SetDiagonal ( const Pds::Vector V )

Copia un vector columna en una diagonal de la matriz. Si los tamaños son diferentes, se interceptan las matrices y se copia solamente en la intersección.

Parámetros

[in] V El vector a copiar.

Devuelve: Retorna true si la copia fue hecha o false si hubo algún problema. En caso de retornar false no se modifica la matriz.

Ejemplos: example_matrix_getset_extras.cpp.

◆ SetDiagonal() [2/2]

bool Pds::Matrix::SetDiagonal ( double val )

Copia un valor en una diagonal de la matriz. Copia hasta donde exista la diagonal.

Parámetros

[in] val El valor a copiar.

Devuelve: Retorna true si la copia fue hecha o false si hubo algún problema. En caso de retornar false no se modifica la matriz.

◆ GetMatrix() [1/2]

Pds::Matrix Pds::Matrix::GetMatrix	(	unsigned int	lin_init,
		unsigned int	col_init,
		unsigned int	lin_end,
		unsigned int	col_end
	)		const

Retorna una sub matriz desde la posición (lin_init,col_init) hasta (lin_end,col_end), inclusive. Hace una verificación si la posición existe, si no existe llena con ceros.

Parámetros

[in]	lin_init	La linea inicial en consulta.
[in]	col_init	La columna inicial en consulta.
[in]	lin_end	La linea final en consulta.
[in]	col_end	La columna final en consulta.

Devuelve: Retorna una sub matriz. Si no existe interseccion entre la matriz y las cordenadas pedidas, entonces se retorna una matriz vacia.

Ejemplos: example_matrix_getset.cpp.

◆ GetMatrix() [2/2]

Pds::Matrix Pds::Matrix::GetMatrix	(	unsigned int	lin_init,
		unsigned int	col_init,
		Pds::Size	size
	)		const

Retorna una sub matriz desde la posición (lin_init,col_init) hasta (lin_end,col_end), inclusive. Hace una verificación si la posición existe, si no existe llena con ceros.

Parámetros

[in]	lin_init	La linea inicial en consulta.
[in]	col_init	La columna inicial en consulta.
[in]	size	Tamaño de la matriz a recibir.

Devuelve: Retorna una sub matriz. Si no existe interseccion entre la matriz y las cordenadas pedidas, entonces se retorna una matriz vacia.

◆ SetMatrix()

bool Pds::Matrix::SetMatrix	(	unsigned int	lin,
		unsigned int	col,
		const Pds::Matrix &	B
	)

Copia en si mismo (A) en la posicion (lin,col), el contenido de una matriz B. Si a matriz B no cabe em A se retorna false.

Parámetros

[in]	lin	Linea donde se inicia a copia.
[in]	col	Columna donde se inicia a copia.
[in]	B	la matriz a copiar

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false no se copia nada. Si IsEmpty() iguala true retorna false.

◆ GetRow() [1/2]

Pds::Matrix Pds::Matrix::GetRow ( unsigned int lin ) const

Retorna una matriz linea escojida en la linea lin. Hace una verificación si la linea existe, si no existe devuelve una matriz vacia.

Parámetros

[in] lin La linea en consulta.

Devuelve: Retorna una matriz linea. Si no existe la linea, entonces se retorna una matriz vacia.

Ejemplos: example_matrix_knearest.cpp.

◆ GetRow() [2/2]

bool Pds::Matrix::GetRow	(	unsigned int	lin,
		Pds::Matrix &	Row
	)		const

Retorna una matriz linea escojida en la linea lin de X. Hace una verificación si la linea existe y si Row es linea, si no existe devuelve false.

Parámetros

[in]	lin	La linea en consulta.
[out]	Row	Una matriz linea. Si la matriz no es linea con columnas igual X.Ncol(), entonces se retorna false.

Devuelve: Retorna true si todo fue bien o false si no (y no modifica nada).

◆ GetRowAsColVector() [1/2]

Pds::Vector Pds::Matrix::GetRowAsColVector ( unsigned int lin ) const

Retorna un vector columna copia de una linea de la matriz.

Parámetros

[in] lin La linea en consulta.

Devuelve: Retorna un vector columna correspondiente a la linea (lin) o un vector vacío si la posición no existe.

Ejemplos: example_mathmatrix_crossentropy.cpp, example_mathmatrix_kldivergence.cpp y example_matrix_getset_extras.cpp.

◆ GetRowAsColVector() [2/2]

bool Pds::Matrix::GetRowAsColVector	(	unsigned int	lin,
		Pds::Vector &	V
	)		const

Retorna un vector columna copia de una linea de la matriz.

Parámetros

[in]	lin	La linea en consulta.
[out]	V	Vector donde se copian los datos de la linea.

Devuelve: Retorna true si la linea existe y el tamañp de V corresponde a número de columnas de la matriz o false en caso contrario.

◆ GetRows() [1/4]

bool Pds::Matrix::GetRows	(	unsigned int	lin_init,
		unsigned int	lin_end,
		Pds::Matrix &	B
	)		const

Retorna una sub matriz escojida desde la linea lin_init hasta lin_end, inclusive. Hace una verificación si la linea existe, si no existe llena esta con ceros.

Parámetros

[in]	lin_init	La linea inicial en consulta.
[in]	lin_end	La linea final en consulta.
[out]	B	Matriz donde se copiarán los datos.

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false no se modifica B. Si no existe interseccion entre la matriz y las lineas pedidas, entonces se retorna false.

Ejemplos: example_matrix_algebra_eig.cpp y example_ra_indices.cpp.

◆ GetRows() [2/4]

Pds::Matrix Pds::Matrix::GetRows	(	unsigned int	lin_init,
		unsigned int	lin_end
	)		const

Retorna una sub matriz escojida desde la linea lin_init hasta lin_end, inclusive. Hace una verificación si la linea existe, si no existe llena esta con ceros.

Parámetros

[in]	lin_init	La linea inicial en consulta.
[in]	lin_end	La linea final en consulta.

Devuelve: Retorna una sub matriz. Si no existe interseccion entre la matriz y las lineas pedidas, entonces se retorna una matriz vacia.

◆ GetRows() [3/4]

Pds::Matrix Pds::Matrix::GetRows ( std::list< unsigned int > List ) const

Retorna una sub matriz escojida desde una lista de indices de lineas. Hace una verificación si los indices existen, si alguno no existe devuelve una matriz vacia.

Parámetros

[in] List La lista de indices de lineas.

Devuelve: Retorna una sub matriz. Si no existe algun elemento en la lista se devuelve una matriz vacia.

◆ GetRows() [4/4]

Pds::Matrix Pds::Matrix::GetRows ( std::vector< unsigned int > Vec ) const

Retorna una sub matriz escojida desde una lista de indices de lineas. Hace una verificación si los indices existen, si alguno no existe devuelve una matriz vacia.

Parámetros

[in] Vec El vector de indices de lineas.

Devuelve: Retorna una sub matriz. Si no existe algun elemento en la lista se devuelve una matriz vacia.

◆ GetRowsRand()

Pds::Matrix Pds::Matrix::GetRowsRand ( unsigned int N ) const

Retorna una sub matriz escojiendo N lineas aleatoriamente (sin repetición).

Atención: La función usa internamente la función rand(), si se desea esta puede ser aleatoriamente inicializada usando la funcíón Pds::Ra::Randomize(), de lo contrario los números pseudo aleatórios siempre seguirán la misma secuencia.

Parámetros

[in] N El número de lineas a escojer.

Devuelve: Retorna una sub matriz. Si N=0 o N>Nlin entonces se retorna una matriz vacia.

◆ GetCol() [1/2]

Pds::Matrix Pds::Matrix::GetCol ( unsigned int col ) const

Retorna una matriz columna escojida en la columna col. Hace una verificación si la columna existe, si no existe devuelve una matriz vacia.

Parámetros

[in] col La columna en consulta.

Devuelve: Retorna una matriz columna. Si no existe la columna, entonces se retorna una matriz vacia.

◆ GetCol() [2/2]

bool Pds::Matrix::GetCol	(	unsigned int	col,
		Pds::Matrix &	MatCol
	)		const

Retorna una matriz columna escojida en la columna col. Hace una verificación si la columna existe y tiene el tamanho de MatCol, si no existe devuelve false.

Parámetros

[in]	col	La columna en consulta.
[out]	MatCol	La columna de la matriz.

Devuelve: Retorna true si todo fue bien o false si no (y no modifica nada).

◆ GetColVector() [1/2]

Pds::Vector Pds::Matrix::GetColVector ( unsigned int col ) const

Retorna un vector columna copia de una columna de la matriz.

Parámetros

[in] col La columna en consulta.

Devuelve: Retorna el vector columna en la posición (col) o un vector vacío si la posición no existe.

Ejemplos: example_matrix_getset_extras.cpp.

◆ GetColVector() [2/2]

bool Pds::Matrix::GetColVector	(	unsigned int	col,
		Pds::Vector &	U
	)		const

Copia a un vector columna el contenido de una columna de la matriz.

Parámetros

[in]	col	La columna en consulta.
[out]	U	Vector donde se copiaran los datos.

Devuelve: Retorna true si todo fue bien o false si no.

◆ GetCols() [1/4]

Pds::Matrix Pds::Matrix::GetCols	(	unsigned int	col_init,
		unsigned int	col_end
	)		const

Retorna una sub matriz escojida desde la columna col_init hasta col_end, inclusive. Hace una verificación si la columna existe, si no existe llena esta con ceros.

Parámetros

[in]	col_init	La columna inicial en consulta.
[in]	col_end	La columna final en consulta.

Devuelve: Retorna una sub matriz. Si no existe interseccion entre la matriz y las columnas pedidas, entonces se retorna una matriz vacia.

Ejemplos: example_ra_indices.cpp.

◆ GetCols() [2/4]

Pds::Matrix Pds::Matrix::GetCols ( std::list< unsigned int > List ) const

Retorna una sub matriz escojida desde una lista de indices de columnas. Hace una verificación si los indices existen, si alguno no existe devuelve una matriz vacia.

Parámetros

[in] List La lista de indices de columnas.

Devuelve: Retorna una sub matriz. Si no existe algun elemento en la lista se devuelve una matriz vacia.

◆ GetCols() [3/4]

Pds::Matrix Pds::Matrix::GetCols ( const std::initializer_list< unsigned int > List ) const

Retorna una sub matriz escojida desde una lista de indices de columnas. Hace una verificación si los indices existen, si alguno no existe devuelve una matriz vacia.

Parámetros

[in] List La lista de indices de columnas.

Devuelve: Retorna una sub matriz. Si no existe algun elemento en la lista se devuelve una matriz vacia.

◆ GetCols() [4/4]

Pds::Matrix Pds::Matrix::GetCols ( std::vector< unsigned int > Vec ) const

Retorna una sub matriz escojida desde una lista de indices de columnas. Hace una verificación si los indices existen, si alguno no existe devuelve una matriz vacia.

Parámetros

[in] Vec El vector de indices de columnas.

Devuelve: Retorna una sub matriz. Si no existe algun elemento en la lista se devuelve una matriz vacia.

◆ GetColsRand()

Pds::Matrix Pds::Matrix::GetColsRand ( unsigned int N ) const

Retorna una sub matriz escojiendo N columnas aleatoriamente (sin repetición).

Atención: La función usa internamente la función rand(), si se desea esta puede ser aleatoriamente inicializada usando la funcíón Pds::Ra::Randomize(), de lo contrario los números pseudo aleatórios siempre seguirán la misma secuencia.

Parámetros

[in] N El número de columnas a escojer.

Devuelve: Retorna una sub matriz. Si N=0 o N>Ncol entonces se retorna una matriz vacia.

◆ SetRowValue()

bool Pds::Matrix::SetRowValue	(	unsigned int	lin,
		double	value
	)

Copia un valor en una linea de la matriz.

Parámetros

[in]	value	El valor a copiar.
[in]	lin	La linea en consulta.

Devuelve: Retorna true si la copia fue hecha y la posición (lin) existe o false si hubo algún problema. En caso de retornar false no se modifica la matriz.

◆ SetRowVector()

bool Pds::Matrix::SetRowVector	(	unsigned int	lin,
		const Pds::Vector &	X
	)

Copia un vector en una linea de la matriz.

Parámetros

[in]	lin	La linea en consulta.
[in]	X	El vector a copiar.

Devuelve: Retorna true si la copia fue hecha y la posición (lin) existe o false si hubo algún problema. En caso de retornar false no se modifica la matriz.

◆ SetColValue()

bool Pds::Matrix::SetColValue	(	unsigned int	col,
		double	value
	)

Copia un valor en una columna de la matriz.

Parámetros

[in]	value	El valor a copiar.
[in]	col	La columna en consulta.

Devuelve: Retorna true si la copia fue hecha y la posición (col) existe o false si hubo algún problema. En caso de retornar false no se modifica la matriz.

◆ SetColVector() [1/3]

bool Pds::Matrix::SetColVector	(	unsigned int	col,
		const Pds::Vector &	V
	)

Copia un vector columna en una columna de la matriz. Si los tamaños son diferentes, se interceptan las matrices y se copia solamente en la intersección.

Parámetros

[in]	V	El vector a copiar.
[in]	col	La columna en consulta.

Devuelve: Retorna true si la copia fue hecha y la posición (col) existe o false si hubo algún problema. En caso de retornar false no se modifica la matriz.

Ejemplos: example_matrix_getset_extras.cpp.

◆ SetColVector() [2/3]

bool Pds::Matrix::SetColVector	(	unsigned int	col,
		double(*)(double)	func,
		const Pds::Vector &	V
	)

Copia un vector columna en una columna de la matriz, despues de evaluar el vector en una funcion. Si los tamaños son diferentes, se interceptan las matrices y se copia solamente en la intersección.

Parámetros

[in]	func	funcion a evaluar.
[in]	V	El vector a evaluar y copiar.
[in]	col	La columna en consulta.

Devuelve: Retorna true si la copia fue hecha y la posición (col) existe o false si hubo algún problema. En caso de retornar false no se modifica la matriz.

◆ SetColVector() [3/3]

bool Pds::Matrix::SetColVector	(	unsigned int	col,
		double(*)(double, double)	func,
		const Pds::Vector &	V,
		double	var
	)

Copia un vector columna en una columna de la matriz, despues de evaluar el vector en una funcion. Si los tamaños son diferentes, se interceptan las matrices y se copia solamente en la intersección.

Parámetros

[in]	func	funcion a evaluar.
[in]	V	El vector a evaluar y copiar.
[in]	var	Segunda variable a evaluar.
[in]	col	La columna en consulta.

Devuelve: Retorna true si la copia fue hecha y la posición (col) existe o false si hubo algún problema. En caso de retornar false no se modifica la matriz.

◆ GetPoint2DsFromCols()

std::vector< Pds::Point2D > Pds::Matrix::GetPoint2DsFromCols	(	unsigned int	colx,
		unsigned int	coly
	)		const

Copia un par de columnas de la matriz para convertirlas en un vector de Pds::Point2D.

Parámetros

[in]	colx	Columna para la coordenada X.
[in]	coly	Columna para la coordenada Y.

Devuelve: Retorna un vector de Pds::Point2D con las coordenadas X e Y.

◆ ToStdVector()

std::vector< double > Pds::Matrix::ToStdVector ( void ) const

Retorna un std::vector con los elelentos de la matriz, lee columna a columna.

Devuelve: Retorna un std::vector con los elelentos de la matriz, lee columna a columna.

◆ RowAddAssig()

bool Pds::Matrix::RowAddAssig	(	unsigned int	lin1,
		unsigned int	lin2,
		double	alpha
	)

Multiplica los valores de la linea lin2 por alfa y el resultado es sumado a los valores de la linea lin1.

$row[lin1] \leftarrow row[lin1]+\alpha ~ row[lin2]$

Parámetros

[in]	lin1	Lineas a intercambiar.
[in]	lin2	Lineas a intercambiar.
[in]	alpha	Factor multiplicador.

Devuelve: Retorna true si todo fue bien o false si no.

◆ RowMulAssig()

bool Pds::Matrix::RowMulAssig	(	unsigned int	lin,
		double	alpha
	)

Multiplica la linea lin por alpha.

$row[lin] \leftarrow \alpha ~ row[lin]$

Parámetros

[in]	lin	Linea a multiplicar.
[in]	alpha	Factor multiplicador.

Devuelve: Retorna true si todo fue bien o false si no.

◆ RowDivAssig()

bool Pds::Matrix::RowDivAssig	(	unsigned int	lin,
		double	alpha
	)

Divide la linea lin por alpha.

$row[lin] \leftarrow row[lin]/\alpha$

Parámetros

[in]	lin	Linea a dividir.
[in]	alpha	Factor multiplicador.

Devuelve: Retorna true si todo fue bien o false si no.

◆ RowSwap()

bool Pds::Matrix::RowSwap	(	unsigned int	lin1,
		unsigned int	lin2
	)

Intercambia los valores de las lineas de una matriz.

Parámetros

[in]	lin1	Lineas a intercambiar.
[in]	lin2	Lineas a intercambiar.

Devuelve: Retorna true si todo fue bien o false si no.

◆ RowSwapBelow()

int Pds::Matrix::RowSwapBelow ( unsigned int n )

Si el n-avo elemento de la diagonal es cero entonces intercambia la linea n de la matriz con cualquier linea inferior con elemento diferente de cero en la columna n.

Parámetros

[in] n Linea a intercambiar.

Devuelve: Retorna el número de la fila con quien intercambio o -1 en caso de error. Si el n-avo elemento de la diagonal ja es diferente de cero no se hace nada y se retorna n.

◆ RowReduction()

bool Pds::Matrix::RowReduction ( void )

Convierte la matriz en una matriz reducida.

Devuelve: Retorna true si todo fue bien o false si no. Si retorna false la matriz es modificada hasta donde consiguió avanzar el proceso de reducción.

◆ RowDivByAbsMax()

bool Pds::Matrix::RowDivByAbsMax ( void )

Normaliza cada linea de la matriz dividiendola por el máximo valor absoluto de la linea. Si la linea tiene solo ceros esta no es modificada.

Devuelve: Retorna true si todo fue bien o false si no. Retorna false quando a matriz esta vazia.

◆ IntegerCount()

std::map< int, unsigned int > Pds::Matrix::IntegerCount ( void ) const

Cuenta la cantidad de elementos enteros.

Devuelve: Cuenta la cantidad de elementos enteros.

Ejemplos: example_matrix_set_map.cpp.

◆ IntegerSet()

std::set< int > Pds::Matrix::IntegerSet ( void ) const

Set de elementos enteros.

Devuelve: Set de elementos enteros.

Ejemplos: example_matrix_set_map.cpp.

◆ MultiplyValues()

double Pds::Matrix::MultiplyValues ( void ) const

Calcula el valor de la multiplicación de elementos en la matriz.

Devuelve: Retorna el valor de la multiplicación de elementos en la matriz. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ Sum()

double Pds::Matrix::Sum ( void ) const

Calcula el valor de la suma de elementos de la matriz.

Devuelve: Retorna el valor de la suma de elementos de la matriz. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_coin_create.cpp, example_exponential_create.cpp, example_normal_create.cpp, example_rayleigh_create.cpp y example_uniform_create.cpp.

◆ Mean()

double Pds::Matrix::Mean ( void ) const

Calcula el valor medio de la matriz.

Devuelve: Retorna el valor medio de la matriz. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_kernel_gaussian.cpp.

◆ MeanInCols()

Pds::Matrix Pds::Matrix::MeanInCols ( void ) const

Calcula el valor medio de las columnas de la matriz.

Devuelve: Retorna una matriz linea con el valor medio de cada columna de la matriz. En caso de que la matriz sea vacía se retorna Pds::Matrix().

◆ MeanInRows()

Pds::Vector Pds::Matrix::MeanInRows ( void ) const

Calcula la media de cada linea de la matriz.

Devuelve: Retorna un vector con la media de cada linea de la matriz.

◆ Std()

double Pds::Matrix::Std ( double * mean = NULL ) const

Calcula el valor del desvío padrón de la matriz.

Devuelve: Retorna el valor del desvío padrón de la matriz. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ StdInRows()

Pds::Vector Pds::Matrix::StdInRows ( void ) const

Calcula el standard deviation de cada linea de la matriz.

Devuelve: Retorna un vector con el standard deviation de cada linea de la matriz.

◆ StdInCols()

Pds::Matrix Pds::Matrix::StdInCols ( void ) const

Calcula el standard deviation de cada columna de la matriz.

Devuelve: Retorna un vector con el standard deviation de cada columna de la matriz.

◆ MeanStdInRows()

bool Pds::Matrix::MeanStdInRows	(	Pds::Vector &	Mean,
		Pds::Vector &	Std
	)		const

Calcula la media y el standard deviation de cada linea de la matriz.

Parámetros

[out]	Mean	Vector con la media de cada linea. El vector debe tener el mismo número de lineas que la matriz caso contrario se retorna false.
[out]	Std	Vector con es standard deviation de cada linea. El vector debe tener el mismo número de lineas que la matriz caso contrario se retorna false.

Devuelve: Retorna tue si todo fue bien o false si no. si se rtorna false, tambien se libera la memoria de Std y Mean.

◆ MeanStdInCols()

bool Pds::Matrix::MeanStdInCols	(	Pds::Matrix &	Mean,
		Pds::Matrix &	Std
	)		const

Calcula la media y el standard deviation de cada linea de la matriz.

Parámetros

[out]	Mean	Vector con la media de cada columna. El vector debe tener el mismo número de lineas que la matriz caso contrario se retorna false.
[out]	Std	Vector con es standard deviation de cada columna. El vector debe tener el mismo número de lineas que la matriz caso contrario se retorna false.

Devuelve: Retorna tue si todo fue bien o false si no. si se rtorna false, tambien se libera la memoria de Std y Mean.

◆ Var()

double Pds::Matrix::Var ( double * mean = NULL ) const

Calcula el valor de la varianza de la matriz.

Devuelve: Retorna el valor de la varianza de la matriz. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ Max()

double Pds::Matrix::Max ( unsigned int * id = NULL ) const

Calcula el máximo valor de la matriz.

Parámetros

[in] id Se retorna el id do valor máximo.

Devuelve: Retorna el máximo valor de la matriz. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_coin_create.cpp, example_exponential_create.cpp, example_rayleigh_create.cpp, example_triangle_evalsamples.cpp y example_triangle_getsamples.cpp.

◆ Min()

double Pds::Matrix::Min ( unsigned int * id = NULL ) const

Calcula el mínimo valor de la matriz.

Parámetros

[in] id Se retorna el id do valor mínimo.

Devuelve: Retorna el mínimo valor de la matriz. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_coin_create.cpp, example_exponential_create.cpp, example_rayleigh_create.cpp, example_triangle_evalsamples.cpp y example_triangle_getsamples.cpp.

◆ MaxAbs()

double Pds::Matrix::MaxAbs ( unsigned int * id = NULL ) const

Calcula el máximo valor del valor absoluto de la matriz.

Parámetros

[in] id Se retorna el id do valor máximo.

Devuelve: Retorna el máximo valor del valor absoluto de la matriz. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ MinAbs()

double Pds::Matrix::MinAbs ( unsigned int * id = NULL ) const

Calcula el mínimo valor del valor absoluto de la matriz.

Parámetros

[in] id Se retorna el id do valor mínimo.

Devuelve: Retorna el mínimo valor del valor absoluto de la matriz. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ MaxInCols() [1/3]

Pds::Matrix Pds::Matrix::MaxInCols ( void ) const

Calcula el máximo en cada columna de la matriz.

Devuelve: Retorna el máximo valor en cada columna de la matriz. En caso de que la matriz sea vacía se retorna Pds::Matrix().

◆ MinInCols() [1/3]

Pds::Matrix Pds::Matrix::MinInCols ( void ) const

Calcula el mínimo en cada columna de la matriz.

Devuelve: Retorna el mínimo valor en cada columna de la matriz. En caso de que la matriz sea vacía se retorna Pds::Matrix().

◆ MaxInCols() [2/3]

Pds::Matrix Pds::Matrix::MaxInCols ( std::vector< unsigned int > & Lin ) const

Calcula el máximo en cada columna de la matriz.

Parámetros

[in] Lin La linea del valor máximo en cada columna.

Devuelve: Retorna el máximo valor en cada columna de la matriz. En caso de que la matriz sea vacía se retorna Pds::Matrix() y Lin tiene tamaño cero.

◆ MinInCols() [2/3]

Pds::Matrix Pds::Matrix::MinInCols ( std::vector< unsigned int > & Lin ) const

Calcula el mínimo en cada columna de la matriz.

Parámetros

[in] Lin La linea del valor mínimo en cada columna.

Devuelve: Retorna el mínimo valor en cada columna de la matriz. En caso de que la matriz sea vacía se retorna Pds::Matrix() y Lin tiene tamaño cero.

◆ MaxInCols() [3/3]

Pds::Matrix Pds::Matrix::MaxInCols ( Pds::Array< unsigned int > & Lin ) const

Calcula el máximo en cada columna de la matriz.

Parámetros

[in] Lin La linea del valor máximo en cada columna.

Devuelve: Retorna el máximo valor en cada columna de la matriz. En caso de que la matriz sea vacía se retorna Pds::Matrix() y Lin tiene tamaño cero.

◆ MinInCols() [3/3]

Pds::Matrix Pds::Matrix::MinInCols ( Pds::Array< unsigned int > & Lin ) const

Calcula el mínimo en cada columna de la matriz.

Parámetros

[in] Lin La linea del valor mínimo en cada columna.

Devuelve: Retorna el mínimo valor en cada columna de la matriz. En caso de que la matriz sea vacía se retorna Pds::Matrix() y Lin tiene tamaño cero.

◆ MaxAbsInCols()

Pds::Matrix Pds::Matrix::MaxAbsInCols ( void ) const

Retorna una matriz con el máximo valor absoluto de cada columna.

Devuelve: Retorna una matriz con el máximo valor absoluto de cada columna.

◆ MaxAbsInRows()

Pds::Vector Pds::Matrix::MaxAbsInRows ( void ) const

Retorna un vector con el máximo valor absoluto de cada linea.

Devuelve: Retorna un vector con el máximo valor absoluto de cada linea.

◆ MinAbsInRows()

Pds::Vector Pds::Matrix::MinAbsInRows ( void ) const

Retorna un vector con el mínimo valor absoluto de cada linea.

Devuelve: Retorna un vector con el mínimo valor absoluto de cada linea.

◆ MaxInRows()

Pds::Vector Pds::Matrix::MaxInRows ( void ) const

Retorna un vector con el máximo valor de cada linea.

Devuelve: Retorna un vector con el máximo valor de cada linea.

◆ MinInRows()

Pds::Vector Pds::Matrix::MinInRows ( void ) const

Retorna un vector con el mínimo valor de cada linea.

Devuelve: Retorna un vector con el mínimo valor de cada linea.

◆ ArgMaxInRows()

Pds::Vector Pds::Matrix::ArgMaxInRows ( void ) const

Retorna un vector con el ID del máximo valor de cada linea.

Devuelve: Retorna un vector con el ID del máximo valor de cada linea. En cado de haber varios máximos, retorna el ID del primero.

◆ ArgMinInRows()

Pds::Vector Pds::Matrix::ArgMinInRows ( void ) const

Retorna un vector con el ID del mínimo valor de cada linea.

Devuelve: Retorna un vector con el ID del mínimo valor de cada linea. En cado de haber varios mínimos, retorna el ID del primero.

◆ ScalingColsAnalysis()

bool Pds::Matrix::ScalingColsAnalysis	(	Pds::Vector &	Mean,
		Pds::Vector &	Std
	)

Calcula la media y el standard deviation de cada columna de la matriz. Si el std de la columna es cero esta no es normalizada.

$Col[i] \leftarrow \frac{Col[i]-Mean[i]}{Std[i]}$

Parámetros

[out]	Mean	Vector con la media de cada columna. El vector debe tener el mismo número de lineas que la matriz caso contrario se retorna false.
[out]	Std	Vector con es standard deviation de cada columna. El vector debe tener el mismo número de lineas que la matriz caso contrario se retorna false.

Devuelve: Retorna tue si todo fue bien o false si no. si se retorna false (incompatibilidad de tamaños), también se libera la memoria de Std, Mean y de la propia matriz.

◆ ScalingColsWith()

bool Pds::Matrix::ScalingColsWith	(	const Pds::Vector &	Mean,
		const Pds::Vector &	Std
	)

Escala cada columna de la matriz usando la media y el standard deviation de cada columna de la matriz. Si el std de la columna es cero esta no es normalizada.

$Col[i] \leftarrow \frac{Col[i]-Mean[i]}{Std[i]}$

Parámetros

[out]	Mean	Vector con la media de cada columna. El vector debe tener el mismo número de lineas que la matriz caso contrario se retorna false.
[out]	Std	Vector con es standard deviation de cada columna. El vector debe tener el mismo número de lineas que la matriz caso contrario se retorna false.

Devuelve: Retorna tue si todo fue bien o false si no. si se retorna false (incompatibilidad de tamaños), también se libera la memoria de Std, Mean y de la propia matriz.

◆ CountRoundEqualIn()

long int Pds::Matrix::CountRoundEqualIn ( const Pds::Matrix & B ) const

Calcula el número de elementos enteros iguales entre las matrices A y B.

$S=Sum(round(A)==round(B));$

Parámetros

[in] B Matriz a procesar.

Devuelve: Retorna S el numero de elementos enteros iguales o -1 en caso de error.

Ejemplos: example_matrixmath.cpp.

◆ Accuracy()

double Pds::Matrix::Accuracy	(	const Pds::Matrix &	B,
		double	Umbral
	)		const

Calcula el valor de la Accuracy entre los elementos de las matrices A (Self) y B. Antes de comprarar las matrices se binarizan con el umbral Umbral. A>Umbral, B>Umbral.

$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}=\frac{Number~of~A==B}{Number~of~elements~in~A}$

TP=True positive TN=True negative FP=False positive FN=False negative

Parámetros

[in]	B	Matriz a procesar.
[in]	Umbral	Umbral de binarización.

Devuelve: Retorna el valor de la Accuracy entre los elementos de las matrices A y B. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan. En caso de que las matrizes no tengan el mismo tamaño se retorna Pds::Ra::Nan.

Ejemplos: example_matrixmath.cpp.

◆ NAccuracy()

double Pds::Matrix::NAccuracy ( const Pds::Matrix & B ) const

Calcula el valor de la Accuracy entre los elementos de las matrices A (Self) y B. Antes de comprarar las matrices se conviertena enteros con round().

$Accuracy=\frac{Number~of~A==B}{Number~of~elements~in~A}$

Parámetros

[in] B Matriz a procesar.

Devuelve: Retorna el valor de la Accuracy entre los elementos de las matrices A y B. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan. En caso de que las matrizes no tengan el mismo tamaño se retorna Pds::Ra::Nan.

Ejemplos: example_matrixmath.cpp.

◆ R2()

double Pds::Matrix::R2 ( const Pds::Matrix & Y ) const

Calcula el coeficiente de determinación o .

$R^2\equiv A.R2(Y)\quad =\quad 1-\frac{\sigma_r^2}{\sigma^2}\quad =\quad 1-\frac{\frac{1}{L}|| \mathbf{A}_{ij}-\mathbf{Y}_{ij}||^2}{Var(\mathbf{A})}$

$-\infty < R^2 < 1$

Varianza $\sigma^2$ , varianza residual $\sigma_r^2$ .

Parámetros

[in] Y Matriz a procesar.

Devuelve: Retorna el coeficiente de determinación entre A e Y. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_algebra_eig2.cpp.

◆ Rf()

double Pds::Matrix::Rf ( const Pds::Matrix & Y ) const

Calcula o .

$Rf\equiv A.Rf(Y)\quad =\quad \frac{\sigma_r}{\sigma}$

$Rf\equiv A.Rf(Y)\quad =\quad \frac{\sqrt{\frac{1}{L}|| \mathbf{A}-\mathbf{Y}||^2}}{Std(\mathbf{A})}$

$0 < Rf < \infty$

Varianza $\sigma^2$ , varianza residual $\sigma_r^2$ .

Parámetros

[in] Y Matriz a procesar.

Devuelve: RetornaRF entre A e Y. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ Mape()

double Pds::Matrix::Mape ( const Pds::Matrix & B ) const

Calcula el error absoluto medio porcentual (Mean Absolute Percentage Error) de una matriz.

$A.Mape()=\frac{100}{N_{total}}\sum \limits_{i} \sum \limits_{j} \left|\frac{a_{ij}-b_{ij}}{a_{ij}}\right|$

$N_{total}$ es el número de elementos no cero en $\mathbf{A}$ . Solo son sumados elementos no cero en $\mathbf{A}$ .

Parámetros

[in] B Matriz a procesar.

Devuelve: Retorna el error absoluto medio porcentual. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ InformationGain()

double Pds::Matrix::InformationGain	(	const std::vector< Pds::Matrix > &	A,
		double	Umbral = `0.5`
	)		const

Retorna el Information Gain entre si mismo B y {A[0],A[1],...,A[N-1]}. Antes de comprarar las matrices se binarizan con el umbral Umbral. A[n]>Umbral, B>Umbral.

$h_b(p)=- p log_2(p)- (1-p) log_2(1-p)$

$IG=h_b(p_{\mathbf{B}})-\sum_{n=0}^{N-1} \frac{N_{\mathbf{A[n]}}}{N_{\mathbf{B}}}h_b(p_{\mathbf{A[n]}})$

Parámetros

[in]	A	vector de matrices. Estas seran binarizadas con Umbral.
[in]	Umbral	Umbral de binarización. A>Umbral.

Devuelve: Retorna el Information Gain entre si mismo B y {A[0],A[1],...,A[N-1]}. En caso de que la matriz sea vacía o algun otro problema se retorna Pds::Ra::Nan.

◆ BinaryEntropy()

double Pds::Matrix::BinaryEntropy ( double umbral ) const

Calcula la entropia binaria de la estadistica de y , la probabilidade de unos y ceros en la matriz despues de ubralizar con >=umbral.

$p_1=\frac{A.Geq(umbral).Sum()}{A.Nel()};\qquad p_0=1-p_1;$

$E=- p_0~log_2(p_0)- p_1~log_2(p_1)$

Parámetros

[in] umbral Umbral de binarización (mayor igual).

Devuelve: Retorna el valor de la entropia binaria. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ P1Probability()

double Pds::Matrix::P1Probability ( double umbral ) const

Calcula la probabilidad binaria , la probabilidade en relación a los unos y ceros en la matriz despues de ubralizar con >=umbral.

$p_1=\frac{A.Geq(umbral).Sum()}{A.Nel()};$

Parámetros

[in] umbral Umbral de binarización (mayor igual).

Devuelve: Retorna el valor de la probabilidad p1. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ BalancedBinaryWeight()

Pds::Matrix Pds::Matrix::BalancedBinaryWeight ( double umbral ) const

Retorna una matriz de pesos para balancear la cantidad de 1s y 0s en la matriz. Los unos y ceros en la matriz son obtenidos despues de ubralizar con >=umbral.

Parámetros

[in] umbral Umbral de binarización (mayor igual).

Devuelve: Retorna una matriz de pesos para balancear la cantidad de 1s y 0s en la matriz.

◆ HistogramIntNorm()

Pds::Vector Pds::Matrix::HistogramIntNorm	(	int	min = `0`,
		int	max = `255`
	)		const

Retorna un vector con el histograma de elementos, desde min hasta max (valores enteros). Elementos con valores round(val) menores a min o mayores a max no son computados en el histograma.

HistogramIntNorm()

Atención: El histograma és normalizado para que la suma sea igual a 1 de modo que pueda ser usada como una relación de probabilidades.

Parámetros

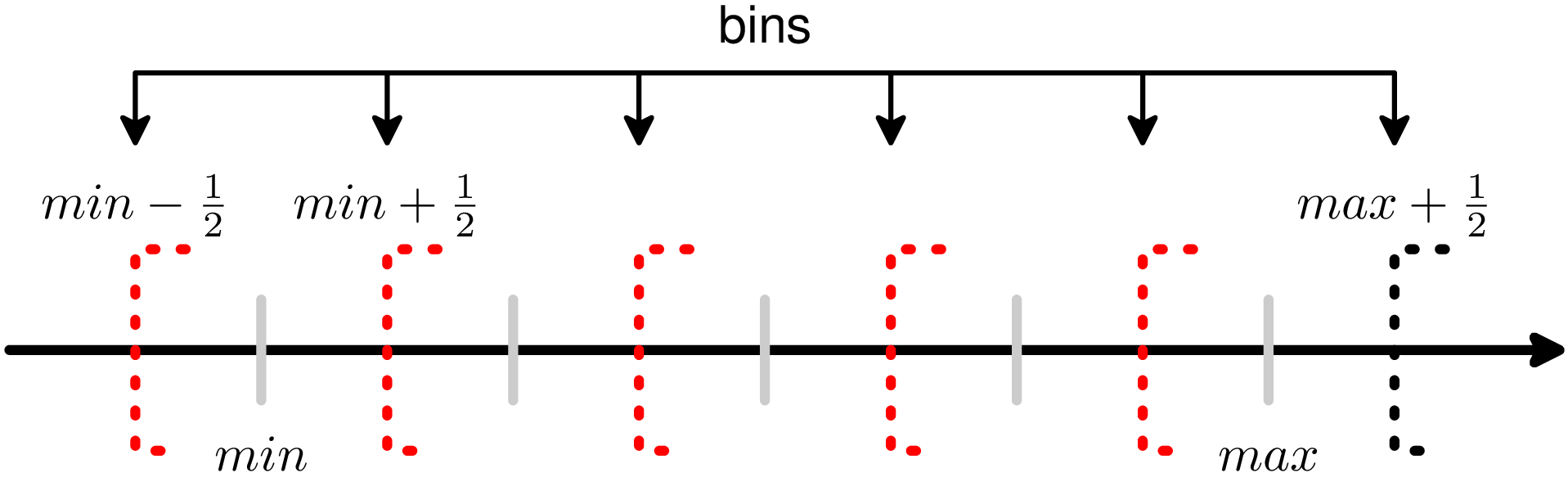
[in]	min	Valor mínimo a ser tomado en cuenta en el histograma. Es obligatorio que .
[in]	max	Valor máximo a ser tomado en cuenta en el histograma. Es obligatorio que .

Devuelve: Retorna una vector con un histograma de .

Ejemplos: example_matrix_dsp2.cpp y example_matrix_dsp_hist.cpp.

◆ Histogram() [1/2]

Pds::Vector Pds::Matrix::Histogram	(	double	min,
		double	max,
		unsigned int	L
	)		const

Retorna un vector con um histograma de elementos espaciados $\delta$ . Elementos con valores menores a $min-\frac{\delta}{2}$ o mayores a $max+\frac{\delta}{2}$ no son computados en el histograma.

$\delta=\frac{max-min}{L-1}$

Histogram(min,max,L)

Parámetros

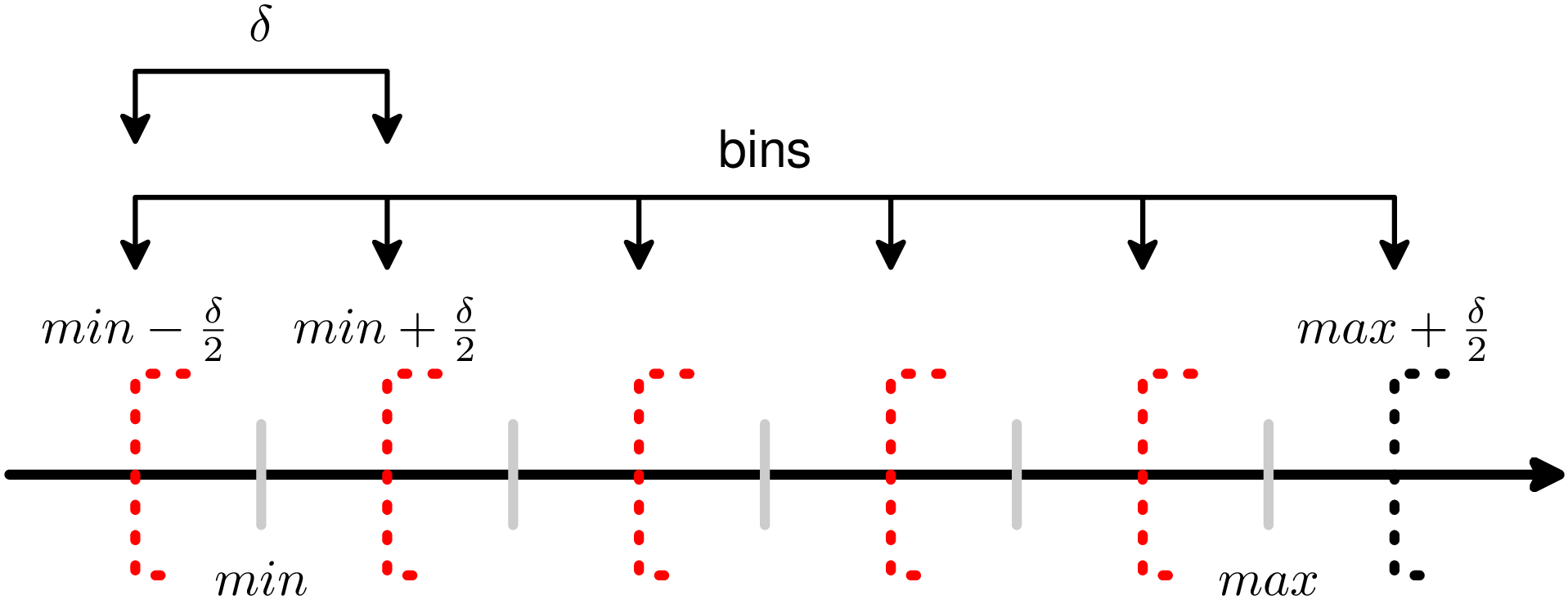
[in]	min	Valor central mínimo a ser tomado en cuenta en el histograma. Es obligatorio que . Si entonces , caso contrario se considera um error.
[in]	max	Valor central máximo a ser tomado en cuenta en el histograma. Es obligatorio que . Si entonces , caso contrario se considera um error.
[in]	L	Número de elementos en el histograma. Es obligatorio que . Para obtener el rango podemos usar $\mathbf{v}=Pds::LinSpace(min,max,L);$ el ambito de $\mathbf{v}[l]$ corresponde a $[\mathbf{v}[l]-\frac{\delta}{2}, \mathbf{v}[l]+\frac{\delta}{2}>$ , donde $\delta=\frac{max-min}{L-1}$

Devuelve: Retorna una vector con un histograma o un vector vacio en caso de error.

Ejemplos: example_coin_create.cpp, example_exponential_create.cpp, example_matrix_dsp_hist.cpp, example_normal_create.cpp, example_rayleigh_create.cpp y example_uniform_create.cpp.

◆ Histogram() [2/2]

Pds::Vector Pds::Matrix::Histogram ( unsigned int L ) const

Retorna un vector con um histograma de elementos espaciados $\delta$ . Elementos con valores menores a o mayores a no son computados en el histograma.

$\delta=\frac{V.Max()-V.Min()}{L}$

Histogram()

Parámetros

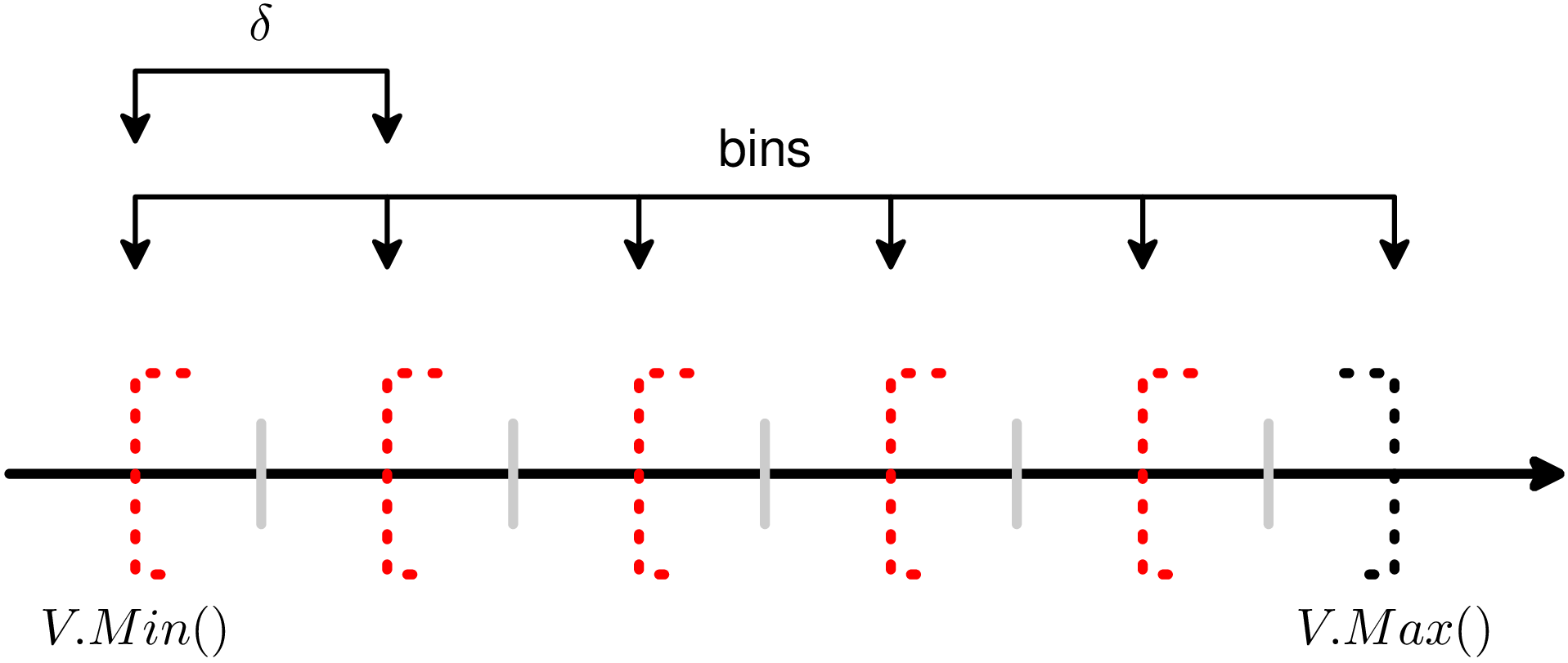
[in] L Número de elementos en el histograma. Es obligatorio que .

Devuelve: Retorna una vector con un histograma o un vector vacio en caso de error.

◆ Corr()

double Pds::Matrix::Corr ( const Pds::Matrix & B ) const

Calcula la correlación de Pearson con la matriz.

$\rho_{A,B}=\frac{cov(A,B)}{\sigma_{A}\sigma_{B}} =\frac{ E[(A-\mu_{A})(B-\mu_{B})] }{ \sigma_{A}\sigma_{B} }$

Parámetros

[in] B Matriz a correlacionar.

Devuelve: Retorna el valor de la correlación. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ Cov()

double Pds::Matrix::Cov ( const Pds::Matrix & B ) const

Calcula la covarianza con la matriz.

$A.Cov(B) \equiv Cov(A,B) = E [ (A-\mu_{A})(B-\mu_{B}) ] = \frac{\sum\limits_i^{Nel} (a_i-\mu_{A})(b_i-\mu_{B})}{Nel-1}$

Parámetros

[in] B Matriz a aplicar covarianza.

Devuelve: Retorna el valor de la covarianza. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ CovMatrix() [1/2]

Pds::Matrix Pds::Matrix::CovMatrix ( void ) const

Calcula la matriz de covarianza de la matriz.

$A \equiv \left( \begin{matrix} \mathbf{a}_{0} ~|~ \mathbf{a}_{1} ~|~... ~|~ \mathbf{a}_{N-1} \end{matrix} \right) \equiv \left( \begin{matrix} \mathbf{r}_{0}\\ \mathbf{r}_{1}\\ \vdots\\ \mathbf{r}_{L-1} \end{matrix} \right)$

$A.CovMatrix()\equiv \left( \begin{matrix} Cov(\mathbf{a}_{0},\mathbf{a}_{0}) & Cov(\mathbf{a}_{0},\mathbf{a}_{1}) & ... & Cov(\mathbf{a}_{0},\mathbf{a}_{N-1})\\ Cov(\mathbf{a}_{1},\mathbf{a}_{0}) & Cov(\mathbf{a}_{1},\mathbf{a}_{1}) & ... & Cov(\mathbf{a}_{1},\mathbf{a}_{N-1})\\ \hdots & \hdots & \hdots & \hdots \\ Cov(\mathbf{a}_{N-1},\mathbf{a}_{0}) & Cov(\mathbf{a}_{N-1},\mathbf{a}_{1}) & ... & Cov(\mathbf{a}_{N-1},\mathbf{a}_{N-1}) \end{matrix} \right) \equiv \frac{1}{L-1}\sum_{l}^{L} (\mathbf{r}_{l}-\mu_{\mathbf{r}})^{T}(\mathbf{r}_{l}-\mu_{\mathbf{r}})$

Devuelve: Retorna el valor de la covarianza. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_algebra_cholesky.cpp y example_matrix_dsp2.cpp.

◆ CovMatrix() [2/2]

Pds::Matrix Pds::Matrix::CovMatrix ( Pds::Matrix & Mean ) const

Calcula la matriz de covarianza de la matriz.

$A \equiv \left( \begin{matrix} \mathbf{a}_{0} ~|~ \mathbf{a}_{1} ~|~... ~|~ \mathbf{a}_{N-1} \end{matrix} \right) \equiv \left( \begin{matrix} \mathbf{r}_{0}\\ \mathbf{r}_{1}\\ \vdots\\ \mathbf{r}_{L-1} \end{matrix} \right)$

$\mu_{\mathbf{r}} \leftarrow \left( \begin{matrix} \mu_{\mathbf{a}_{0}} ~~ \mu_{\mathbf{a}_{1}} ~~... ~~ \mu_{\mathbf{a}_{N-1}} \end{matrix} \right) \equiv \frac{1}{L}\sum_{l}^{L} \mathbf{r}_{l}$

$Cov(\mathbf{a}_i,\mathbf{a}_j) \equiv E [ (\mathbf{a}_i-\mu_{\mathbf{a}_i})(\mathbf{a}_j-\mu_{\mathbf{a}_j}) ]$

$A.CovMatrix()\equiv \left( \begin{matrix} Cov(\mathbf{a}_{0},\mathbf{a}_{0}) & Cov(\mathbf{a}_{0},\mathbf{a}_{1}) & ... & Cov(\mathbf{a}_{0},\mathbf{a}_{N-1})\\ Cov(\mathbf{a}_{1},\mathbf{a}_{0}) & Cov(\mathbf{a}_{1},\mathbf{a}_{1}) & ... & Cov(\mathbf{a}_{1},\mathbf{a}_{N-1})\\ \hdots & \hdots & \hdots & \hdots \\ Cov(\mathbf{a}_{N-1},\mathbf{a}_{0}) & Cov(\mathbf{a}_{N-1},\mathbf{a}_{1}) & ... & Cov(\mathbf{a}_{N-1},\mathbf{a}_{N-1}) \end{matrix} \right) \equiv \frac{1}{L-1}\sum_{l}^{L} (\mathbf{r}_{l}-\mu_{\mathbf{r}})^{T}(\mathbf{r}_{l}-\mu_{\mathbf{r}})$

Parámetros

[out] Mean Matriz $\mu_{\mathbf{r}}$ con las medias de cada columna, también pode ser entendido como la media de todas las filas.

Devuelve: Retorna el valor de la covarianza. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ XCorr()

Pds::Matrix Pds::Matrix::XCorr	(	const Pds::Matrix &	B,
		bool	Same = `false`
	)		const

Calcula la correlacion cruzada entre A y B.

$\mathbf{A}\equiv [a(i,j)] ,\qquad \mathbf{A}.Size()\equiv \{L_A,C_A\}$

$\mathbf{B}\equiv [b(i,j)] ,\qquad \mathbf{B}.Size()\equiv \{L_B,C_B\}$

$\mathbf{D}\equiv [d(i-(L_B-1),j-(C_B-1))] ,\qquad \mathbf{D}.Size()\equiv \{L_B+L_A-1,C_B+C_A-1\}$

XCorr
Image	Formulation
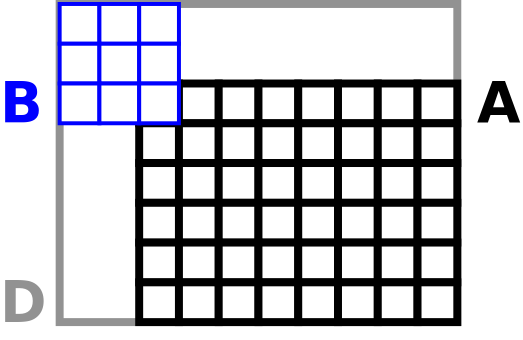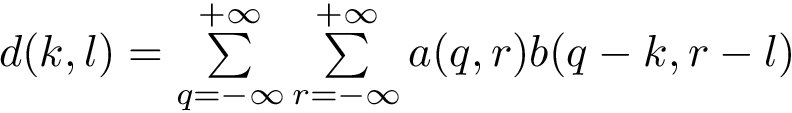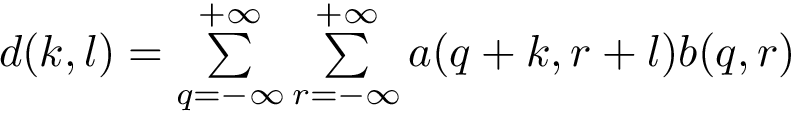	$d(k,l)=\sum \limits_{q=-\infty}^{+\infty} \sum \limits_{r=-\infty}^{+\infty} a(q,r) b(q-k,r-l)$ $d(k,l)=\sum \limits_{q=-\infty}^{+\infty} \sum \limits_{r=-\infty}^{+\infty} a(q+k,r+l) b(q,r)$

Exemplo:

$\mathbf{A}.Size()\equiv \{6,6\} \quad \mathbf{B}.Size()\equiv \{3,3\}$

$\mathbf{D}=\left(\begin{array}{cc|cccccc} d(-2,-2) & d(-2,-1) & d(-2,0) & d(-2,1) & d(-2,2) & d(-2,3) & d(-2,4) & d(-2,5) \\ d(-1,-2) & d(-1,-1) & d(-1,0) & d(-1,1) & d(-1,2) & d(-1,3) & d(-1,4) & d(-1,5) \\ \hline d(0,-2) & d(0,-1) & d(0,0) & d(0,1) & d(0,2) & d(0,3) & d(0,4) & d(0,5) \\ d(1,-2) & d(1,-1) & d(1,0) & d(1,1) & d(1,2) & d(1,3) & d(1,4) & d(1,5) \\ d(2,-2) & d(2,-1) & d(2,0) & d(2,1) & d(2,2) & d(2,3) & d(2,4) & d(2,5) \\ d(3,-2) & d(3,-1) & d(3,0) & d(3,1) & d(3,2) & d(3,3) & d(3,4) & d(3,5) \\ d(4,-2) & d(4,-1) & d(4,0) & d(4,1) & d(4,2) & d(4,3) & d(4,4) & d(4,5) \\ d(5,-2) & d(5,-1) & d(5,0) & d(5,1) & d(5,2) & d(5,3) & d(5,4) & d(5,5) \\ \end{array}\right)$

Atención: Esta funcion no usa FFT para economizar el tiempo.

Parámetros

[in]	B	Matriz a aplicar la correlacion cruzada.
[in]	Same	indica si la correlación cruzada tendrá el mismo tamaño que A, si Same es igual a true entonces, $\mathbf{D}.Size()\equiv \{Nlin,Ncol\}$ . Por defecto Same es igual a false.

Devuelve: retorna la correlacion cruzada.

Ejemplos: example_matrix_dsp2.cpp.

◆ Conv()

Pds::Matrix Pds::Matrix::Conv	(	const Pds::Matrix &	B,
		Pds::Ra::Padding	Padding = `Pds::Ra::Full`
	)		const

Calcula la convolución entre A y B.

$\mathbf{A}\equiv [a(i,j)] ,\qquad \mathbf{A}.Size()\equiv \{L_A,C_A\}$

$\mathbf{B}\equiv [b(i,j)] ,\qquad \mathbf{B}.Size()\equiv \{L_B,C_B\}$

$\mathbf{D}\equiv [d(k,l)]$

$d(k,l)=\sum \limits_{q=-\infty}^{+\infty} \sum \limits_{r=-\infty}^{+\infty} a(k-q,l-r) b(q,r)$

Conv
Padding	Formulation	ID
Pds::Ra::Valid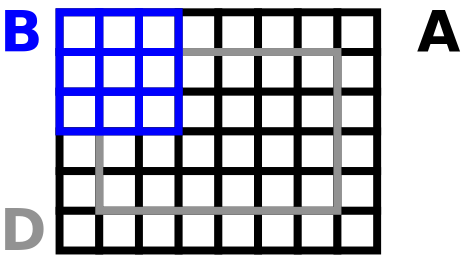	$\mathbf{D}.Size() \equiv \left\{ L_A-L_B+1 , C_A-C_B+1 \right\}$	$\begin{matrix} \textbf{for}~k: L_B-1~\rightarrow~L_A-1\\ \textbf{for}~l: C_B-1~\rightarrow~C_A-1 \end{matrix}$
Pds::Ra::Same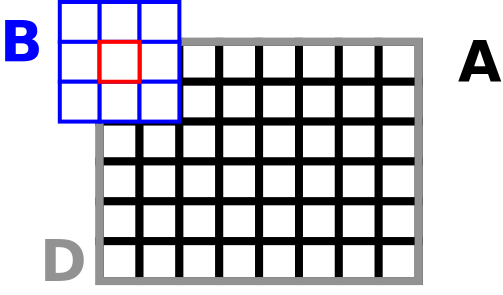	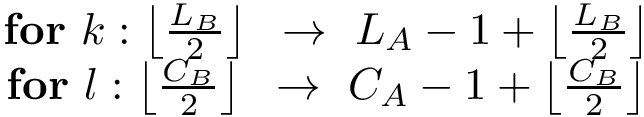$\mathbf{D}.Size() \equiv \left\{ L_A, C_A \right\}$	$\begin{matrix} \textbf{for}~k: \left\lfloor \frac{L_B}{2} \right\rfloor ~\rightarrow~L_A-1+\left\lfloor \frac{L_B}{2} \right\rfloor\\ \textbf{for}~l: \left\lfloor \frac{C_B}{2} \right\rfloor ~\rightarrow~C_A-1+\left\lfloor \frac{C_B}{2} \right\rfloor \end{matrix}$
Pds::Ra::Full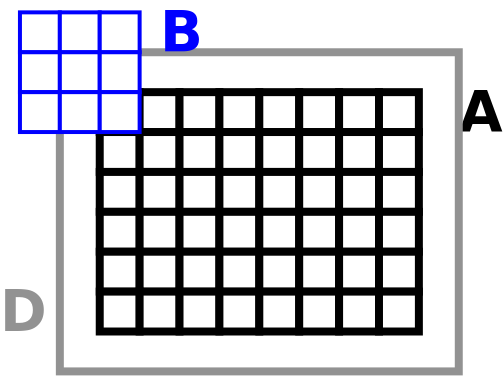	$\mathbf{D}.Size() \equiv \left\{ L_A+L_B -1 , C_A+C_B -1 \right\}$	$\begin{matrix} \textbf{for}~k: 0 ~\rightarrow~L_A+L_B-2\\ \textbf{for}~l: 0 ~\rightarrow~C_A+C_B-2 \end{matrix}$

Atención: Esta funcion NO usa FFT.

Parámetros

[in]	B	Matriz a aplicar la convolución.
[in]	Padding	indica el tipo de pading de la convolución lo cual afecta al tamaño de la matriz de salida.

Devuelve: retorna la convolución.

Ejemplos: example_matrix_dsp_conv.cpp.

◆ Conv2DOutputSize()

static Pds::Size Pds::Matrix::Conv2DOutputSize	(	const Pds::Size &	A,
		const Pds::Size &	B,
		const std::vector< unsigned int > &	Strides,
		Pds::Ra::Padding	Padding
	)

static

Calcula el tamaño de la matriz resultado de la convolucion de A y B.

$Strides \equiv \{S_L,S_C\}$

$\mathbf{A}\equiv [a(i,j)] ,\qquad \mathbf{A}.Size()\equiv \{L_A,C_A\}$

$\mathbf{B}\equiv [b(i,j)] ,\qquad \mathbf{B}.Size()\equiv \{L_B,C_B\}$

$\mathbf{D}\equiv [d(k,l)]$

$d(k,l)=\sum \limits_{q=-\infty}^{+\infty} \sum \limits_{r=-\infty}^{+\infty} a(k-q,l-r) b(q,r)$

Conv2D
Padding	Size	ID
Pds::Ra::Valid	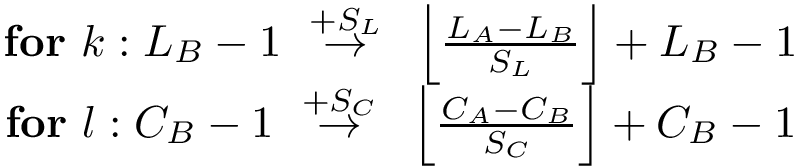$\mathbf{D}.Size() \equiv \left\{ \left\lfloor\frac{L_A-L_B+S_L}{S_L}\right\rfloor, \left\lfloor\frac{C_A-C_B+S_C}{S_C}\right\rfloor \right\}$	$\begin{matrix} \textbf{for}~k: L_B-1~\overset{+S_L}{\rightarrow}~\left\lfloor\frac{L_A-L_B}{S_L}\right\rfloor + L_B-1\\ \textbf{for}~l: C_B-1~\overset{+S_C}{\rightarrow}~\left\lfloor\frac{C_A-C_B}{S_C}\right\rfloor + C_B-1 \end{matrix}$
Pds::Ra::Same	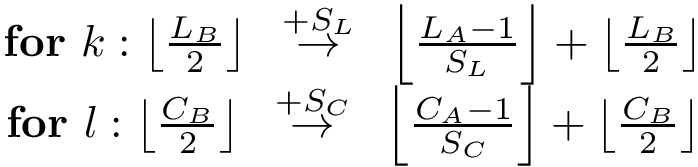$\mathbf{D}.Size() \equiv \left\{ \left\lfloor\frac{L_A-1+S_L}{S_L}\right\rfloor, \left\lfloor\frac{C_A-1+S_C}{S_C}\right\rfloor \right\}$	$\begin{matrix} \textbf{for}~k: \left\lfloor \frac{L_B}{2} \right\rfloor ~\overset{+S_L}{\rightarrow}~ \left\lfloor\frac{L_A-1}{S_L}\right\rfloor+\left\lfloor \frac{L_B}{2} \right\rfloor\\ \textbf{for}~l: \left\lfloor \frac{C_B}{2} \right\rfloor ~\overset{+S_C}{\rightarrow}~ \left\lfloor\frac{C_A-1}{S_C}\right\rfloor+\left\lfloor \frac{C_B}{2} \right\rfloor \end{matrix}$
Pds::Ra::Full	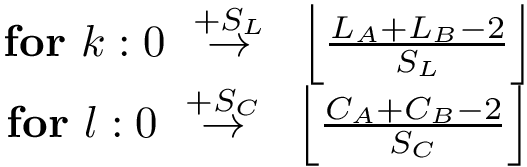$\mathbf{D}.Size() \equiv \left\{ \left\lfloor\frac{L_A + L_B -2 +S_L}{S_L}\right\rfloor, \left\lfloor\frac{C_A + C_B -2 +S_C}{S_C}\right\rfloor \right\}$	$\begin{matrix} \textbf{for}~k: 0 ~\overset{+S_L}{\rightarrow}~\left\lfloor\frac{L_A+L_B-2}{S_L}\right\rfloor \\ \textbf{for}~l: 0 ~\overset{+S_C}{\rightarrow}~\left\lfloor\frac{C_A+C_B-2}{S_C}\right\rfloor \end{matrix}$

Parámetros

[in]	A	Tamaño de la matriz a aplicar la convolución.
[in]	B	Tamaño de la matriz kernel a aplicar la convolución.
[in]	Strides	Paso del convolucionador.
[in]	Padding	indica el tipo de pading de la convolución lo cual afecta al tamaño de la matriz de salida.

Devuelve: retorna el tamaño de la convolución.

Ejemplos: example_matrix_dsp.cpp.

◆ Conv2D() [1/2]

Pds::Matrix Pds::Matrix::Conv2D	(	const Pds::Matrix &	B,
		const std::vector< unsigned int > &	Strides = `{1, 1}`,
		Pds::Ra::Padding	Padding = `Pds::Ra::Full`
	)		const

Calcula la convolución entre A y B.

$Strides \equiv \{S_L,S_C\}$

$\mathbf{A}\equiv [a(i,j)] ,\qquad \mathbf{A}.Size()\equiv \{L_A,C_A\}$

$\mathbf{B}\equiv [b(i,j)] ,\qquad \mathbf{B}.Size()\equiv \{L_B,C_B\}$

$\mathbf{D}\equiv [d(k,l)]$

$d(k,l)=\sum \limits_{q=-\infty}^{+\infty} \sum \limits_{r=-\infty}^{+\infty} a(k-q,l-r) b(q,r)$

Conv2D
Padding	Size	ID
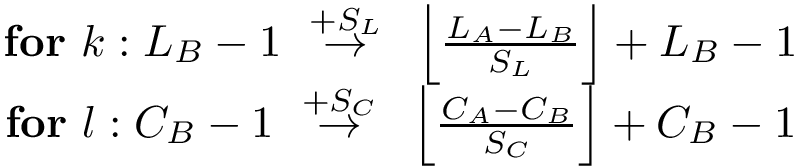Pds::Ra::Valid	$\mathbf{D}.Size() \equiv \left\{ \left\lfloor\frac{L_A-L_B+S_L}{S_L}\right\rfloor, \left\lfloor\frac{C_A-C_B+S_C}{S_C}\right\rfloor \right\}$	$\begin{matrix} \textbf{for}~k: L_B-1~\overset{+S_L}{\rightarrow}~\left\lfloor\frac{L_A-L_B}{S_L}\right\rfloor + L_B-1\\ \textbf{for}~l: C_B-1~\overset{+S_C}{\rightarrow}~\left\lfloor\frac{C_A-C_B}{S_C}\right\rfloor + C_B-1 \end{matrix}$
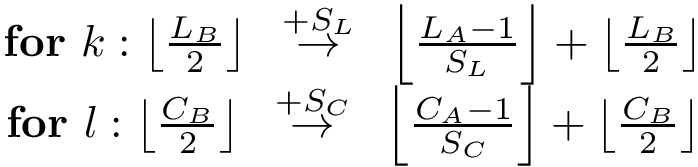Pds::Ra::Same	$\mathbf{D}.Size() \equiv \left\{ \left\lfloor\frac{L_A-1+S_L}{S_L}\right\rfloor, \left\lfloor\frac{C_A-1+S_C}{S_C}\right\rfloor \right\}$	$\begin{matrix} \textbf{for}~k: \left\lfloor \frac{L_B}{2} \right\rfloor ~\overset{+S_L}{\rightarrow}~ \left\lfloor\frac{L_A-1}{S_L}\right\rfloor+\left\lfloor \frac{L_B}{2} \right\rfloor\\ \textbf{for}~l: \left\lfloor \frac{C_B}{2} \right\rfloor ~\overset{+S_C}{\rightarrow}~ \left\lfloor\frac{C_A-1}{S_C}\right\rfloor+\left\lfloor \frac{C_B}{2} \right\rfloor \end{matrix}$
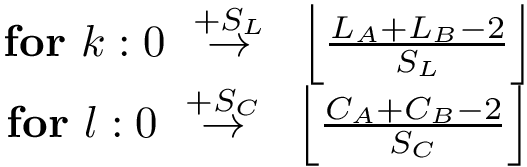Pds::Ra::Full	$\mathbf{D}.Size() \equiv \left\{ \left\lfloor\frac{L_A + L_B -2 +S_L}{S_L}\right\rfloor, \left\lfloor\frac{C_A + C_B -2 +S_C}{S_C}\right\rfloor \right\}$	$\begin{matrix} \textbf{for}~k: 0 ~\overset{+S_L}{\rightarrow}~\left\lfloor\frac{L_A+L_B-2}{S_L}\right\rfloor \\ \textbf{for}~l: 0 ~\overset{+S_C}{\rightarrow}~\left\lfloor\frac{C_A+C_B-2}{S_C}\right\rfloor \end{matrix}$

Atención: Esta funcion NO usa FFT.

Parámetros

[in]	B	Matriz a aplicar la convolución.
[in]	Strides	Paso del convolucionador.
[in]	Padding	indica el tipo de pading de la convolución lo cual afecta al tamaño de la matriz de salida.

Devuelve: retorna la convolución.

Ejemplos: example_matrix_dsp.cpp y example_matrix_dsp_conv2d.cpp.

◆ Conv2D() [2/2]

bool Pds::Matrix::Conv2D	(	const Pds::Matrix &	B,
		Pds::Matrix &	C,
		const std::vector< unsigned int > &	Strides = `{1, 1}`,
		Pds::Ra::Padding	Padding = `Pds::Ra::Full`
	)		const

Calcula la convolución entre A y B.

$Strides \equiv \{S_L,S_C\}$

$\mathbf{A}\equiv [a(i,j)] ,\qquad \mathbf{A}.Size()\equiv \{L_A,C_A\}$

$\mathbf{B}\equiv [b(i,j)] ,\qquad \mathbf{B}.Size()\equiv \{L_B,C_B\}$

$\mathbf{D}\equiv [d(k,l)]$

$d(k,l)=\sum \limits_{q=-\infty}^{+\infty} \sum \limits_{r=-\infty}^{+\infty} a(k-q,l-r) b(q,r)$

Conv2D
Padding	Size	ID
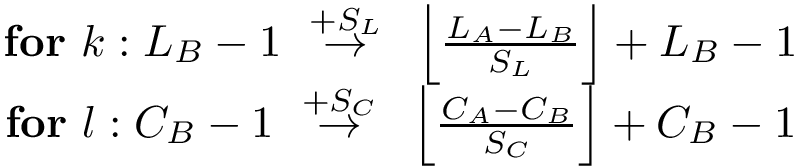Pds::Ra::Valid	$\mathbf{D}.Size() \equiv \left\{ \left\lfloor\frac{L_A-L_B+S_L}{S_L}\right\rfloor, \left\lfloor\frac{C_A-C_B+S_C}{S_C}\right\rfloor \right\}$	$\begin{matrix} \textbf{for}~k: L_B-1~\overset{+S_L}{\rightarrow}~\left\lfloor\frac{L_A-L_B}{S_L}\right\rfloor + L_B-1\\ \textbf{for}~l: C_B-1~\overset{+S_C}{\rightarrow}~\left\lfloor\frac{C_A-C_B}{S_C}\right\rfloor + C_B-1 \end{matrix}$
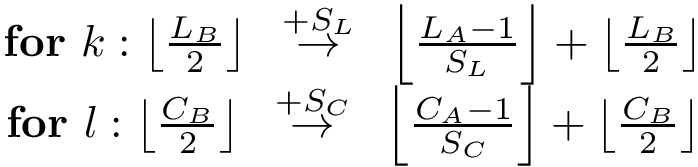Pds::Ra::Same	$\mathbf{D}.Size() \equiv \left\{ \left\lfloor\frac{L_A-1+S_L}{S_L}\right\rfloor, \left\lfloor\frac{C_A-1+S_C}{S_C}\right\rfloor \right\}$	$\begin{matrix} \textbf{for}~k: \left\lfloor \frac{L_B}{2} \right\rfloor ~\overset{+S_L}{\rightarrow}~ \left\lfloor\frac{L_A-1}{S_L}\right\rfloor+\left\lfloor \frac{L_B}{2} \right\rfloor\\ \textbf{for}~l: \left\lfloor \frac{C_B}{2} \right\rfloor ~\overset{+S_C}{\rightarrow}~ \left\lfloor\frac{C_A-1}{S_C}\right\rfloor+\left\lfloor \frac{C_B}{2} \right\rfloor \end{matrix}$
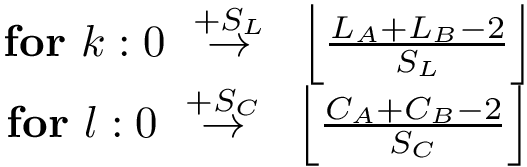Pds::Ra::Full	$\mathbf{D}.Size() \equiv \left\{ \left\lfloor\frac{L_A + L_B -2 +S_L}{S_L}\right\rfloor, \left\lfloor\frac{C_A + C_B -2 +S_C}{S_C}\right\rfloor \right\}$	$\begin{matrix} \textbf{for}~k: 0 ~\overset{+S_L}{\rightarrow}~\left\lfloor\frac{L_A+L_B-2}{S_L}\right\rfloor \\ \textbf{for}~l: 0 ~\overset{+S_C}{\rightarrow}~\left\lfloor\frac{C_A+C_B-2}{S_C}\right\rfloor \end{matrix}$

Atención: Esta funcion NO usa FFT.

Parámetros

[in]	B	Matriz a aplicar la convolución.
[out]	C	Matriz de salida con la convolución. Esta debe tener el tamaño adecuado o se retornará false.
[in]	Strides	Paso del convolucionador.
[in]	Padding	indica el tipo de pading de la convolución lo cual afecta al tamaño de la matriz de salida.

Devuelve: retorna true si todo fue bien o false si no.

◆ MaxPooling()

Pds::Matrix Pds::Matrix::MaxPooling	(	unsigned int	LinPool,
		unsigned int	ColPool
	)		const

Aplica max pooling de la matriz $\mathbf{A}$ de $L_\mathbf{A}$ lineas y $C_\mathbf{A}$ columnas.

La matriz resultante $\mathbf{B}$ tendrá $L_\mathbf{B}=ceil(L_\mathbf{A}/LinPool)$ lineas y $C_\mathbf{B}=ceil(C_\mathbf{A}/ColPool)$ columnas.

Parámetros

[in]	LinPool	Pooling entre lineas.
[in]	ColPool	Pooling entre columnas.

Devuelve: Retorna la matriz B resultado de aplicar maxpooling.

Ejemplos: example_matrix_dsp.cpp.

◆ FilterMean()

Pds::Matrix Pds::Matrix::FilterMean ( unsigned int r ) const

Procesa la matriz A usando un filtro mean de radio r.

$B[i,j]=\frac{1}{(2 r+1)^2} \left( \begin{matrix} 1 & 1 & ... & 1 & 1\\ 1 & 1 & ... & 1 & 1\\ \vdots & \vdots & ... & \vdots & \vdots \\ 1 & 1 & ... & 1 & 1\\ 1 & 1 & ... & 1 & 1 \end{matrix} \right)$

Atención: Este filtro tambien es llamado: Mean filtering, Smoothing, Averaging, Box filtering

Parámetros

[in] r Radio de accion de la media, es decir kernel de tamaño (2r+1)x(2r+1).

Devuelve: Retorna la matriz B resultado de procesar la matriz A con un filtro mean de radio 1.

◆ FilterMean3()

Pds::Matrix Pds::Matrix::FilterMean3 ( void ) const

Procesa la matriz A usando un filtro mean de radio 1.

$B[i,j]=\frac{1}{9} \left( \begin{matrix} A[i-1,j-1]&+&A[i-1,j]&+&A[i-1,j+1]&+\\ A[i ,j-1]&+&A[i ,j]&+&A[i ,j+1]&+\\ A[i+1,j-1]&+&A[i+1,j]&+&A[i+1,j+1]&~ \end{matrix} \right)$

Atención: Este filtro tambien es llamado: Mean filtering, Smoothing, Averaging, Box filtering

Devuelve: Retorna la matriz B resultado de procesar la matriz A con un filtro mean de radio 1.

◆ Resize()

Pds::Matrix Pds::Matrix::Resize ( double factor ) const

Retorna una matriz B (size: NlinB,NcolB) resultado de aplicar un subsampling de la matriz A (size: Nlin,Ncol) por un factor.

$1 \leq factor \leq 2$

$NlinB=\left\lfloor\frac{Nlin}{factor}\right\rfloor,\qquad NcolB=\left\lfloor\frac{Ncol}{factor}\right\rfloor.$

Es aplicado el método de bilinear y luego linear entre la aproximacion espacial y la version reduzida por 2.

Parámetros

[in] factor Este factor debe estar entre 1 y 2 inclusive, de lo contrario da error.

Devuelve: Retorna la matriz B resultado de procesar la matriz A. o una vacia en caso de error.

◆ QR()

bool Pds::Matrix::QR	(	Pds::Matrix &	Q,
		Pds::Matrix &	R
	)		const

Calcula la descomposición QR de una matriz $A \in \mathrm{R}^{M \times N}$ .

$\mathbf{A}= \left( \begin{matrix} \mathbf{a_1} ~|~ \mathbf{a_2} ~|~ ...~|~ \mathbf{a_N}\\ \end{matrix} \right) =\mathbf{Q}\mathbf{R}$

donde

$\mathbf{Q}= \left( \begin{matrix} \mathbf{q_1} ~|~ \mathbf{q_2} ~|~ ... ~|~ \mathbf{q_N}\\ \end{matrix} \right) \in \mathrm{R}^{M \times N}, \qquad \mathbf{q_i}^T \mathbf{q_j}=0, \quad \forall i\neq j$

$\mathbf{R}= \left( \begin{matrix} ||\mathbf{u_1}|| & <\mathbf{q_1},\mathbf{a_2}> & <\mathbf{q_1},\mathbf{a_3}> & ... & <\mathbf{q_1},\mathbf{a_N}>\\ 0 & ||\mathbf{u_2}|| & <\mathbf{q_2},\mathbf{a_3}> & ... & <\mathbf{q_2},\mathbf{a_N}>\\ 0 & 0 & ||\mathbf{u_3}|| & ... & <\mathbf{q_3},\mathbf{a_N}>\\ \vdots & \vdots & \vdots & ... & \vdots\\ 0 & 0 & 0 & ... & ||\mathbf{u_N}||\\ \end{matrix} \right) \in \mathrm{R}^{N \times N}$

mediante el siguiente algoritmo:

$\mathbf{u_k} = \mathbf{a_k} - \sum_{j=1}^{k-1} <\mathbf{q_j},\mathbf{a_k}> \mathbf{q_j}, \qquad \mathbf{q_k}= \frac{\mathbf{u_k}}{||\mathbf{u_k}||}, \qquad k \in \{1,~2,~3,~...,~N\}$

Parámetros

[out]	Q	Una matriz con columnas ortogonales.
[out]	R	Una matriz triangular superior.

Devuelve: Retorna true si la descomposición QR fue existosa y false si nó.

◆ CholeskyBanachiewicz()

Pds::Matrix Pds::Matrix::CholeskyBanachiewicz ( void ) const

Dada una matriz simétrica definida positiva $\mathbf{A}$ , este método realiza la descomposición Cholesky, especificamente Cholesky-Banachiewicz.

$\mathbf{A}\equiv \mathbf{L} \mathbf{L}^{T}$

Devuelve: Retorna la matriz triangular inferior $\mathbf{L}$ con elementos positivos en la diagonal.

Ejemplos: example_matrix_algebra_cholesky.cpp.

◆ CholeskyCrout()

Pds::Matrix Pds::Matrix::CholeskyCrout ( void ) const

Dada una matriz simétrica definida positiva $\mathbf{A}$ , este método realiza la descomposición Cholesky, especificamente Cholesky-Crout.

$\mathbf{A}\equiv \mathbf{L} \mathbf{L}^{T}$

Devuelve: Retorna la matriz triangular inferior $\mathbf{L}$ con elementos positivos en la diagonal.

Ejemplos: example_matrix_algebra_cholesky.cpp.

◆ HessenbergReduction()

Pds::Matrix Pds::Matrix::HessenbergReduction ( void ) const

Dada una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ , este metodo retorna una Matriz de Hessenberg ( $\mathbf{H} \in \mathrm{R}^{N \times N}$ ) semejante a la matriz $\mathbf{A}$ . La matriz $\mathbf{H}$ es calculada siguiendo la Householder transformation.

$\mathbf{A}= \begin{bmatrix} a_{11} & a_{12} & a_{13} & ... & a_{1N} \\ a_{21} & a_{22} & a_{23} & ... & a_{2N} \\ a_{31} & a_{32} & a_{33} & ... & a_{3N} \\ a_{41} & a_{42} & a_{43} & ... & a_{4N} \\ a_{51} & a_{52} & a_{53} & ... & a_{5N} \\ \dots & \dots & \dots & ... & \dots \\ a_{N1} & a_{N2} & a_{N3} & ... & a_{NN} \\ \end{bmatrix} \rightarrow \mathbf{P}^{-1}\mathbf{A}\mathbf{P}= \mathbf{H}= \begin{bmatrix} h_{11} & h_{12} & h_{13} & ... & h_{1N} \\ h_{21} & h_{22} & h_{23} & ... & h_{2N} \\ 0 & h_{32} & h_{33} & ... & h_{3N} \\ 0 & 0 & h_{43} & ... & h_{4N} \\ 0 & 0 & 0 & ... & h_{5N} \\ \dots & \dots & \dots & ... & \dots \\ 0 & 0 & 0 & ... & h_{NN} \\ \end{bmatrix}$

$\begin{array}{l} \mathbf{H}\leftarrow \mathbf{A}\\ for~k=~0,~1,~..,~N-3\\ \qquad\begin{aligned} \alpha &=-\operatorname {sgn} \left(h_{k+1,k}\right){\sqrt {\sum _{j=k+1}^{N-1}h_{jk}^{2}}};\\ r &=\sqrt{ \frac{1}{2}\left(\alpha^{2}-h_{k+1,k}~\alpha \right) };\\ v_0 & =v_1=...=v_k=0;\\ v_{k+1} & = \frac{h_{k+1,k}-\alpha}{2r}\\ v_{j} & = \frac{h_{jk}}{2r}, \quad for~j=k+2,k+3,...,N-1\\ \mathbf{P} & = \mathbf{I} - 2 \mathbf{v}~\mathbf{v}^T\\ \mathbf{A} & \leftarrow \mathbf{P} \mathbf{A} \mathbf{P} \end{aligned}\\ endfor \end{array}$

Devuelve: Retorna una Matriz de Hessenberg ( $\mathbf{H}$ ) semelhante a la matriz $\mathbf{A}$ .

◆ SubLambdaI()

Pds::Matrix Pds::Matrix::SubLambdaI ( double lambda ) const

Dada una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ , este metodo retorna :

$\mathbf{B} \leftarrow \mathbf{A} - \lambda \mathbf{I}$

Devuelve: Retorna la matriz $\mathbf{B}$ .

◆ AddLambdaI()

Pds::Matrix Pds::Matrix::AddLambdaI ( double lambda ) const

Dada una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ , este metodo retorna :

$\mathbf{B} \leftarrow \mathbf{A} + \lambda \mathbf{I}$

Devuelve: Retorna la matriz $\mathbf{B}$ .

◆ QuadraticForm()

double Pds::Matrix::QuadraticForm ( const Pds::Vector & x ) const

Calcula la forma cuadrática $\mathbf{x}^{T} \mathbf{A} \mathbf{x}$ .

$r\leftarrow \mathbf{x}^{T} \mathbf{A} \mathbf{x}$

Parámetros

[in] x El vector a multiplicar.

Devuelve: Retorna el valor . En caso de que la matriz esté vacía, o no sea cuadrada, se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_algebra3.cpp.

◆ QuadraticFormWithRows() [1/2]

Pds::Vector Pds::Matrix::QuadraticFormWithRows ( const Pds::Matrix & X ) const

Calcula la forma cuadrática $\mathbf{x}_{l}^{T} \mathbf{A} \mathbf{x}_{l}$ .

$y_l \leftarrow \mathbf{x}_{l}^{T} \mathbf{A} \mathbf{x}_{l}$

$\mathbf{X} \equiv \left[ \begin{array}{l} \mathbf{x}_{0}^{T}\\ \mathbf{x}_{1}^{T}\\ \mathbf{x}_{2}^{T}\\ \vdots\\ \mathbf{x}_{l}^{T}\\ \vdots\\ \mathbf{x}_{L-1}^{T}\\ \end{array} \right] \qquad \mathbf{Y} \equiv \left[ \begin{array}{l} y_{0}\\ y_{1}\\ y_{2}\\ \vdots\\ y_{l}\\ \vdots\\ y_{L-1}\\ \end{array} \right]$

Parámetros

[in] X La matriz $\mathbf{X}$ con los vectores a multiplicar.

Devuelve: Retorna el valor . En caso de que la matriz esté vacía, o no sea cuadrada, se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_algebra3.cpp y example_matrix_algebra4.cpp.

◆ QuadraticFormWithRows() [2/2]

Pds::Vector Pds::Matrix::QuadraticFormWithRows	(	const Pds::Matrix &	X,
		const Pds::Vector &	Mu
	)		const

Calcula la forma cuadrática $\mathbf{x}_{l}^{T} \mathbf{A} \mathbf{x}_{l}$ .

$y_l \leftarrow (\mathbf{x}_{l}-\mathbf{\mu})^{T} \mathbf{A} (\mathbf{x}_{l}-\mathbf{\mu})$

$\mathbf{X} \equiv \left[ \begin{array}{l} \mathbf{x}_{0}^{T}\\ \mathbf{x}_{1}^{T}\\ \mathbf{x}_{2}^{T}\\ \vdots\\ \mathbf{x}_{l}^{T}\\ \vdots\\ \mathbf{x}_{L-1}^{T}\\ \end{array} \right] \qquad \mathbf{Y} \equiv \left[ \begin{array}{l} y_{0}\\ y_{1}\\ y_{2}\\ \vdots\\ y_{l}\\ \vdots\\ y_{L-1}\\ \end{array} \right]$

Parámetros

[in]	X	La matriz $\mathbf{X}$ con los vectores a multiplicar.
[in]	Mu	El vector media $\mathbf{\mu}$ .

Devuelve: Retorna un vector $\mathbf{Y}$ .

◆ QuadraticFormWithSamples()

Pds::Matrix Pds::Matrix::QuadraticFormWithSamples	(	const std::vector< Pds::Matrix > &	X,
		const Pds::Vector &	Mu
	)		const

Calcula la forma cuadrática $\mathbf{x}_{l}^{T} \mathbf{A} \mathbf{x}_{l}$ .

$y_l \leftarrow (\mathbf{x}_{l}-\mathbf{\mu})^{T} \mathbf{A} (\mathbf{x}_{l}-\mathbf{\mu})$

$[Pds::Vector(\mathbf{X}[0]),~...,~Pds::Vector(\mathbf{X}[N-1])] \equiv \left[ \begin{array}{l} \mathbf{x}_{0}^{T}\\ \mathbf{x}_{1}^{T}\\ \mathbf{x}_{2}^{T}\\ \vdots\\ \mathbf{x}_{l}^{T}\\ \vdots\\ \mathbf{x}_{L-1}^{T}\\ \end{array} \right] \qquad \mathbf{Y} \equiv \left[ \begin{array}{l} y_{0}\\ y_{1}\\ y_{2}\\ \vdots\\ y_{l}\\ \vdots\\ y_{L-1}\\ \end{array} \right].Reshape(Nlin,Ncol);$

Parámetros

[in]	X	Las matrices $\mathbf{X}$ con los vectores a multiplicar.
[in]	Mu	El vector media $\mathbf{\mu}$ .

Devuelve: Retorna la matriz $\mathbf{Y}$ . En caso de que la matriz esté vacía, o no sea cuadrada, se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_algebra4.cpp.

◆ QuadraticDotWithRows()

Pds::Vector Pds::Matrix::QuadraticDotWithRows ( const Pds::Vector & Mu ) const

Calcula la forma cuadrática $\mathbf{x}_{l}^{T} \mathbf{x}_{l}$ .

$y_l \leftarrow (\mathbf{x}_{l}-\mathbf{\mu})^{T} (\mathbf{x}_{l}-\mathbf{\mu})$

$\mathbf{X} \equiv \left[ \begin{array}{l} \mathbf{x}_{0}^{T}\\ \mathbf{x}_{1}^{T}\\ \mathbf{x}_{2}^{T}\\ \vdots\\ \mathbf{x}_{l}^{T}\\ \vdots\\ \mathbf{x}_{L-1}^{T}\\ \end{array} \right] \qquad \mathbf{Y} \equiv \left[ \begin{array}{l} y_{0}\\ y_{1}\\ y_{2}\\ \vdots\\ y_{l}\\ \vdots\\ y_{L-1}\\ \end{array} \right]$

Parámetros

[in] Mu El vector media $\mathbf{\mu}$ .

Devuelve: Retorna el valor . En caso de que la matriz esté vacía, o no sea cuadrada, se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_algebra3.cpp.

◆ MaxAbsOfLowerTriangular()

double Pds::Matrix::MaxAbsOfLowerTriangular ( void ) const

Retorna el máximo valor absoluto de los elementos abajo de la diagonal. La matriz no necesita ser cuadrada, lo elementos abajo de la diagonal se revisan hasta donde se pueda.

Devuelve: Retorna el máximo valor absoluto de los elementos abajo de la diagonal. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_algebra3.cpp.

◆ MaxAbsOfDiag()

double Pds::Matrix::MaxAbsOfDiag ( void ) const

Retorna el máximo valor absoluto de la diagonal de una matriz $\mathbf{A}$ . La matriz no necesita ser cuadrada, la diagonal se revisa hasta donde se pueda.

$r = max(diag(|\mathbf{A}|))$

Devuelve: Retorna el máximo valor absoluto de la diagonal de $\mathbf{A}$ . En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_algebra3.cpp.

◆ MinAbsOfDiag()

double Pds::Matrix::MinAbsOfDiag ( void ) const

Retorna el mínimo valor absoluto de la diagonal de una matriz $\mathbf{A}$ . La matriz no necesita ser cuadrada, la diagonal se revisa hasta donde se pueda.

$r = min(diag(|\mathbf{A}|))$

Devuelve: Retorna el mínimo valor absoluto de la diagonal de $\mathbf{A}$ . En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_algebra3.cpp.

◆ MinOfDiag()

double Pds::Matrix::MinOfDiag ( void ) const

Retorna el valor mínimo de la diagonal de una matriz cuadrada $\mathbf{A}$ .

$r = min(diag(\mathbf{A}))$

Devuelve: Retorna el valor mínimo de la diagonal de $\mathbf{A}$ . En caso de que la matriz sea vacía o no sea cuadrada se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_algebra3.cpp.

◆ Det()

double Pds::Matrix::Det ( void ) const

Calcula la determinante.

$A.Det() = |A|$

Devuelve: Retorna la determinante de un vector. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_algebra.cpp.

◆ Dot()

double Pds::Matrix::Dot ( const Pds::Matrix & B ) const

Calcula el producto punto entre dos matrices.

$A.Dot(B) = \sum \limits_{i,j} a_{i,j}b_{i,j}$

Parámetros

[in] B Matriz a multiplicar.

Devuelve: Retorna el producto punto. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_matrix_operaterows.cpp.

◆ RMS()

double Pds::Matrix::RMS ( void ) const

Calcula valor raiz quadrático medio de una matriz.

$A.RMS()=\sqrt{\frac{1}{Nlin~Ncol}\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}|}^2}$

Devuelve: Retorna el valor raiz cuadrático medio. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ MeanAbsolute()

double Pds::Matrix::MeanAbsolute ( void ) const

Calcula valor absoluto medio de una matriz.

$A.MeanAbsolute()=\frac{1}{Nlin~Ncol}\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}|}$

Devuelve: Retorna el valor absoluto medio. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ MeanSquare()

double Pds::Matrix::MeanSquare ( void ) const

Calcula valor quadrático medio de una matriz.

$A.MeanSquare()=\frac{1}{Nlin~Ncol}\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}|}^2$

Devuelve: Retorna el valor cuadrático medio. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ MSE()

double Pds::Matrix::MSE ( const Pds::Matrix & B ) const

Calcula valor del error quadrático medio (Mean Square Error) entre las matrices y .

$MSE= A.MSE(B)= \frac{1}{Nlin~Ncol}\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}-b_{ij}|}^2$

Parámetros

[in] B Matriz a comparar con el padrón A.

Devuelve: Retorna el valor del error cuadrático medio. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

Ejemplos: example_optadam_create.cpp.

◆ RMSE()

double Pds::Matrix::RMSE ( const Pds::Matrix & B ) const

Calcula valor de la raiz cuadrada del error quadrático medio (Root Mean Square Error) entre las matrices y .

$RMSE= A.RMSE(B)= \sqrt{\frac{1}{Nlin~Ncol}\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}-b_{ij}|}^2 }$

Parámetros

[in] B Matriz a comparar con el padrón A.

Devuelve: Retorna el valor de la raiz cuadrada del error cuadrático medio. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ PSNR()

double Pds::Matrix::PSNR	(	const Pds::Matrix &	B,
		unsigned int	NBITS
	)		const

Calcula valor del error quadrático medio entre las matrices y .

$MSE= A.MeanSquareError(B)= \frac{1}{Nlin~Ncol}\sum \limits_{i}^{Nlin} \sum \limits_{j}^{Ncol} {|a_{ij}-b_{ij}|}^2$

$PSNR= 20~log_{10}\left(\frac{2^{NBITS}-1}{\sqrt{MSE}}\right)$

Parámetros

[in]	B	Matriz a comparar con el padrón A.
[in]	NBITS	Número de bits en que la matriz tiene su escala. ex. si A va de 0 a 255, entonces NBITS=8.

Devuelve: Retorna el valor del error cuadrático medio. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ SumSquare()

double Pds::Matrix::SumSquare ( void ) const

Calcula valor de la suma quadrática de una matriz.

$A.SumSquare()=\sum \limits_{i} \sum \limits_{j} {|a_{ij}|}^2$

Devuelve: Retorna la suma cuadrática. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ SumSquareInRows()

Pds::Vector Pds::Matrix::SumSquareInRows ( void ) const

Calcula la suma cuadrada de cada linea de la matriz.

Devuelve: Retorna un vector con la suma cuadrada de cada linea de la matriz.

◆ NormDiff()

double Pds::Matrix::NormDiff ( const Pds::Matrix & B ) const

Calcula la 2-norm de una matriz (Frobenius norm).

$||A-B||_2=\sqrt{\sum \limits_{i} \sum \limits_{j} {|a_{ij}-b_{ij}|}^2}$

]

Parámetros

[in] B Una matriz del mismo tamaño que la que invoca el método.

Devuelve: Retorna la norma de la diferencia de dos matrices. En caso de error se retorna Pds::Ra::Nan.

◆ NormDiff2()

double Pds::Matrix::NormDiff2 ( const Pds::Matrix & B ) const

Calcula la 2-norm al cuadrado de una matriz.

$||A-B||_2^2={\sum \limits_{i} \sum \limits_{j} {|a_{ij}-b_{ij}|}^2}$

Parámetros

[in] B Una matriz del mismo tamaño que la que invoca el método.

Devuelve: Retorna la norma de la diferencia de dos matrices. En caso de error se retorna Pds::Ra::Nan.

◆ Norm()

double Pds::Matrix::Norm ( void ) const

Calcula la 2-norm de una matriz (Frobenius norm).

$||A||_2=\sqrt{\sum \limits_{i} \sum \limits_{j} {|a_{ij}|}^2}$

Devuelve: Retorna la norma de un vector. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ PNorm1()

double Pds::Matrix::PNorm1 ( void ) const

Calcula la 1-norm de un vector.

$||A||_1=\max \limits_{j} \sum \limits_{i} {|a_{ij}|}$

Devuelve: Retorna la norma de un vector. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ PNormInf()

double Pds::Matrix::PNormInf ( void ) const

Calcula la inf-norm de una matriz.

$||A||_{\infty}=\max \limits_{i} \sum \limits_{j} {|a_{ij}|}$

Devuelve: Retorna la norma de un vector. En caso de que la matriz sea vacía se retorna Pds::Ra::Nan.

◆ Normalize()

bool Pds::Matrix::Normalize ( void )

Normaliza la matriz convirtiendolo en una matriz unitaria.

$\mathbf{A}\leftarrow \frac{\mathbf{A}}{||\mathbf{A}||}$

Devuelve: retorna true si todo fue bien o false si no.

◆ NormalizeRows()

bool Pds::Matrix::NormalizeRows ( void )

Normaliza cada linea de la matriz convirtiendolo en una linea unitaria.

$\mathbf{row}\leftarrow \frac{\mathbf{row}}{||\mathbf{A}||}$

Devuelve: retorna true si todo fue bien o false si no.

Ejemplos: example_matrix_algebra.cpp.

◆ MultiIndex()

Pds::Vector Pds::Matrix::MultiIndex ( const Pds::Vector & d ) const

Dada una matriz $\mathbf{X}=\left[\mathbf{x}_1,\quad \mathbf{x}_2,\quad ...,\quad \mathbf{x}_n,\quad ...,\quad \mathbf{x}_N\right]$ es calculado el vector $\mathbf{\overline{X}}^{\mathbf{d}}$ .

$\mathbf{\overline{X}}^{\mathbf{d}}\equiv \mathbf{x}_1^{d_1} \mathbf{x}_2^{d_2} \mathbf{x}_3^{d_3} ... \mathbf{x}_N^{d_N}$

Parámetros

[in] d Vector de indices $\mathbf{d}=\left[d_1,\quad d_2,\quad ...,\quad d_n,\quad ...,\quad d_N\right]$ .

Devuelve: Retorna el vector $\mathbf{\overline{X}}^{\mathbf{d}}$ . En caso de error se retorna una matriz vazia.

Ejemplos: example_matrix_algebra.cpp.

◆ EigenValues()

Pds::Vector Pds::Matrix::EigenValues	(	unsigned int	MaxIter = `2048`,
		double	MinFactor = `0.00001`,
		bool	SortAsc = `true`
	)		const

Calcula los valores própios (Eigenvalues) de una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ siguiendo el algoritmo shift QR, El resultado en la diagonal de $\mathbf{A}^{(k+1)}$ es cargado en el vector $\boldsymbol{\lambda} \in \mathrm{R}^{N}$ .

Atención: Este método solo funciona si los valores própios son reales.

$\begin{array}{l} \mathbf{A}^{(0)} \leftarrow HessenbergReduction(\mathbf{A})\\ ~\\ k=0\\ \mathbf{do:}\\ \qquad\begin{aligned} \mu & \leftarrow \mathbf{q_{N-1}}^T \mathbf{A}^{(k)} \mathbf{q_{N-1}}\\ \{\mathbf{Q},\mathbf{R}\} & \leftarrow \mathbf{A}^{(k)}-\mu \mathbf{I}\\ \mathbf{A}^{(k+1)} & \leftarrow \mathbf{R}\mathbf{Q}+ \mu \mathbf{I}\\ ~ & ~\\ MAX & \leftarrow max~lowtri(|\mathbf{A}^{(k+1)}|)\\ MIN & \leftarrow min~diag(|\mathbf{A}^{(k+1)}|) \end{aligned}\\ \qquad if (MAX==0)\quad \mathbf{break};\\ \mathbf{while}(MAX>MIN\times MinFactor~\mathbf{and}~k< MaxIter)\\ ~\\ \boldsymbol{\lambda} \leftarrow diag\left(\mathbf{A}^{(k+1)}\right) \end{array}$

Parámetros

[in]	MaxIter	Máximo número de iteraciones en el bucle.
[in]	MinFactor	Mínimo factor para salir del bucle.
[in]	SortAsc	Ordena los eigenvalores de forma ascendente si true.

Devuelve: Retorna un vector $\boldsymbol{\lambda}$ . o un vector vacio en caso de error. Es error si la matriz de entrada está vacia o no es quadrada. Los elementos en el vector son retornados en orden ascendente.

Ejemplos: example_matrix_algebra_cholesky.cpp, example_matrix_algebra_eig.cpp y example_matrix_algebra_eig2.cpp.

◆ EigenVectors()

Pds::Matrix Pds::Matrix::EigenVectors	(	const Pds::Vector &	Lambda,
		unsigned int	MaxIter = `20000`,
		bool	EmptyWhenError = `true`
	)		const

Calcula los vectores própios (Eigenvectors) de una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ , Los vectores propios están colocados en las columnas de la matriz $\mathbf{V} \in \mathrm{R}^{N \times K}$ .

$\qquad\begin{aligned} MaxIter & \leftarrow 1000\\ \mathbf{v}_{k} & \leftarrow rand(-1,1);\\ \mathbf{v}_{k} & \leftarrow A.EigenVector_RegInvIter(\lambda_{k},\mathbf{v}_{k},MaxIter);\\ \mathbf{v} & \leftarrow [],~if(\mathbf{v}_{k}.IsEmpty()) \end{aligned}$

Atención: El algoritmo usa internamente Pds::Matrix::EigenVector_RegInvIter();

Parámetros

[in]	Lambda	Un vector con auto valores, $0<K\leq N$ .
[in]	MaxIter	Máximo número de iteraciones.
[in]	EmptyWhenError	Si true retorna vacio cuando hay errores en el cáculo, si false retorna un vector como esté.

Devuelve: Retorna una matriz $\mathbf{V}\in \mathbb{R}^{N\times K}$ con vectores propios en las columnas. o una matriz vacia en caso de error. Es error si la matriz de entrada está vacia o no es quadrada.

Ejemplos: example_matrix_algebra_eig.cpp.

◆ EigenVector_RegInvIter()

Pds::Vector Pds::Matrix::EigenVector_RegInvIter	(	double	lambda,
		const Pds::Vector &	v0,
		unsigned int	MaxIter = `20000`,
		bool	EmptyWhenError = `true`
	)		const

Calcula un autovector (Eigenvector) de una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ . Internamente usa version regularizada del algoritmo Inverse iteration

Atención: El algoritmo puede dar problemas si lambda tiene mutiplicidad, debido a que el algoritmo puede convergir a un mismo autovector, para evitar esto debe intentarse partir desde distintos hasta encontrar dos autovectores que no sean linearmente independientes.

$\begin{array}{l} \alpha \leftarrow 0.001\\ \mathbf{BtB} \leftarrow (\mathbf{A}-\lambda \mathbf{I})^T(\mathbf{A}-\lambda \mathbf{I})\\ do\{\\ \qquad\begin{aligned} \mathbf{M} & \leftarrow \mathbf{BtB} +\alpha \mathbf{I}\\ \alpha & \leftarrow 4 ~\alpha \end{aligned}\\ \}while(\mathbf{M}.DontHaveInv());\\ ~\\ \mathbf{v} \leftarrow \mathbf{v}_{0}\\ Iter \leftarrow 0\\ do\{\\ \qquad\begin{aligned} \mathbf{v}_{last} & \leftarrow \mathbf{v} \\ \mathbf{v} & \leftarrow \mathbf{M}^{-1} \mathbf{v} \\ \mathbf{v} & \leftarrow \frac{\mathbf{v}}{||\mathbf{v}||} \\ ~&~\\ \mathbf{v} & \leftarrow rand(-1,1),~while(\mathbf{v}\equiv \mathbf{0})\\ Iter&++ \\ Rf & \leftarrow \frac{\sqrt{\frac{1}{L}|| \mathbf{v}-\mathbf{v}_{last}||^2}}{\sqrt{\frac{1}{L}|| \mathbf{v}||^2}}\\ \end{aligned}\\ ~\\ \}while \left( ~ \left( Rf >0.0001 \right) and \left( Iter<MaxIter \right) ~\right) ;\\ ~ \\ if\left( Rf \leq 0.00001 \right) \qquad return \quad \mathbf{v};\\ else \qquad \qquad return \quad []; \end{array}$

Parámetros

[in]	lambda	Un autovalor $\lambda$ .
[in]	v0	El valor inicial del autovector a buscar.
[in]	MaxIter	Máximo número de iteraciones.
[in]	EmptyWhenError	Si true retorna vacio cuando hay errores en el cáculo, si false retorna un vector como esté.

Devuelve: Retorna una matriz $\mathbf{V}$ con los vectores propios. o una matriz vacia en caso de error. Es error si la matriz de entrada está vacia o no es quadrada.

◆ EigenDominant()

Pds::Vector Pds::Matrix::EigenDominant	(	double &	lambda,
		unsigned int	MaxIter = `20000`
	)		const

Calcula el autovector (Eigenvector) y el autovalor (Eigenvalue) dominante en una matriz $\mathbf{A} \in \mathrm{R}^{N \times N}$ . Internamente usa el algoritmo Power iteration

$\begin{array}{l} \mathbf{v}\leftarrow rand(-1,1)\\ Iter \leftarrow 0\\ do\{\\ \qquad\begin{aligned} \mathbf{v}&\leftarrow \mathbf{A} \mathbf{v}\\ \mathbf{v}&\leftarrow \frac{\mathbf{v}}{||\mathbf{v}||}\\ \end{aligned}\\ ~\\ \}while \left( ~ \left( Rf >0.0001 \right) and \left( Iter<MaxIter \right) ~\right) ;\\ ~ \\ if\left( Rf \leq 0.00001 \right) \\ \{\\ \qquad \lambda \leftarrow \mathbf{v}^T \mathbf{A} \mathbf{v}\\ \qquad return \quad \mathbf{v};\\ \}\\ else \qquad return \quad []; \end{array}$

Parámetros

[out]	lambda	Retorna el autovalor dominante $\lambda$ si $\mathbf{v}$ no está vacio.
[in]	MaxIter	Máximo número de iteraciones.

Devuelve: Retorna una matriz $\mathbf{V}$ con el vectore propio dominante. o una matriz vacia en caso de error. Es error si la matriz de entrada está vacia o no es quadrada.

Ejemplos: example_matrix_algebra_eig.cpp.

◆ Find()

std::vector< unsigned int > Pds::Matrix::Find ( void ) const

Retorna una lista de indices donde existe un 1 en la matriz A.

Devuelve: Retorna una lista de indices donde existe un 1 en la matriz A.

◆ FindIdOfKMin() [1/2]

std::vector< unsigned int > Pds::Matrix::FindIdOfKMin ( unsigned int K ) const

Retorna un vector de indices de los K menores valores en la matriz A.

Parámetros

[in] K Cantidad de valores mínimos en consulta.

Devuelve: Retorna una lista de indices de los K menores valores en la matriz A.

◆ FindIdOfKMin() [2/2]

std::vector< unsigned int > Pds::Matrix::FindIdOfKMin	(	unsigned int	K,
		std::vector< double > &	dat
	)		const

Retorna un vector de indices de los K menores valores en la matriz A.

Parámetros

[in]	K	Cantidad de valores mínimos en consulta.
[out]	dat	Vector de valores correspondientes a los indices de los K menores valores en la matriz A.

Devuelve: Retorna una lista de indices de los K menores valores en la matriz A.

◆ FindRows()

Pds::Matrix Pds::Matrix::FindRows	(	const Pds::Vector &	B,
		double	b = `0.5`
	)		const

Retorna una nueva matriz con las lineas donde existe un 1 en la matriz B. En verdad B es binarizado internamente con (B>b). La matriz debe tener el mismo número de lineas de B caso contrario se retorna una matriz vacia.

Parámetros

[in]	B	Vector con datos de lineas utiles.
[in]	b	Umbral de binarización de un vector B.

Devuelve: Retorna una nueva matriz con las lineas donde existe un 1 en la matriz B.

Ejemplos: example_matrixfunc.cpp.

◆ FindVal()

Pds::Matrix Pds::Matrix::FindVal ( double val ) const

Retorna una nueva matriz B (binaria) con unos donde exista en A el valor val, y cero donde no se cumpla esta condición.

Parámetros

[in] val Valor a buscar.

Devuelve: Retorna una nueva matriz B con unos donde exista en A el valor val, y cero donde no se cumpla esta condición.

◆ FindValAndReplace()

bool Pds::Matrix::FindValAndReplace	(	double	val,
		double	rep
	)

Remplaza valores especificos por una matriz por otros.

Parámetros

[in]	val	Valor a buscar.
[in]	rep	Valor a colocar en vez de val.

Devuelve: True si todo fue bien o false si no.

◆ FindRowsBlock() [1/3]

std::vector< Pds::Matrix > Pds::Matrix::FindRowsBlock ( const Pds::Vector & V ) const

Retorna un vector de matrices con las lineas donde existe un mismo id en el vector . En verdad es convertido a entero usando la función round(). La matriz debe tener el mismo número de lineas de caso contrario se retorna una matriz vacia.

Parámetros

[in] V Vector con datos de lineas utiles.

Devuelve: Retorna una std::vector<Pds::Matrix> con dos matrices con las lineas donde existe un 0 y un 1 en la matriz .

◆ FindRowsBlock() [2/3]

std::vector< Pds::Matrix > Pds::Matrix::FindRowsBlock	(	const Pds::Vector &	V,
		std::vector< int > &	Label
	)		const

Retorna un vector de matrices con las lineas donde existe un mismo id en el vector . En verdad es convertido a entero usando la función round(). La matriz debe tener el mismo número de lineas de caso contrario se retorna una matriz vacia.

Parámetros

[in]	V	Vector con datos de lineas utiles.
[in]	Label	Vector con datos de label en que le correstonde a cada matriz en la el vector std::vector<Pds::Matrix>.

Devuelve: Retorna una std::vector<Pds::Matrix> con dos matrices con las lineas donde existe un 0 y un 1 en la matriz .

◆ FindRowsBlock() [3/3]

std::vector< Pds::Matrix > Pds::Matrix::FindRowsBlock ( const Pds::Array< unsigned int > & ID ) const

Retorna un grupo de matrices con las lineas donde existe el mismo indice id en la matriz entera . La matriz debe tener el mismo número de lineas que elementos en caso contrario se retorna una matriz vacia.

Atención: Si contiene los valore , quiere decir que en std::vector<Pds::Matrix> M, las matrices y estarán vacías.

Parámetros

[in] ID Matriz con datos con indices (grupos).

Devuelve: Retorna un grupo de matrices, std::vector<Pds::Matrix>, con las lineas donde existe el mismo indice id en la matriz entera .

◆ Apply() [1/6]

bool Pds::Matrix::Apply ( const Pds::Matrix & B )

Aplica la función func a cada elemento de la matriz. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada.

$A \leftarrow B$

Parámetros

[in] B Matriz a evaluar.

Devuelve: true si todo fue bien o false si la matriz era vacia o si no tiene el mismo tamaño que B.

◆ Apply() [2/6]

bool Pds::Matrix::Apply	(	double	Alpha,
		const Pds::Matrix &	B
	)

Aplica la función func a cada elemento de la matriz. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada.

$A \leftarrow \alpha B$

Parámetros

[in]	Alpha	Factor a multiplicar.
[in]	B	Matriz a evaluar.

Devuelve: true si todo fue bien o false si la matriz era vacia o si no tiene el mismo tamaño que B.

◆ Apply() [3/6]

bool Pds::Matrix::Apply ( double(*)(double) func )

Aplica la función func a cada elemento de la matriz.

$A \leftarrow func(A)$

Parámetros

[in] func Función a aplicar, esta debe tener a forma double func(double).

Devuelve: true si todo fue bien o false si la matriz era vacia.

◆ Apply() [4/6]

bool Pds::Matrix::Apply	(	double(*)(double)	func,
		const Pds::Matrix &	B
	)

Aplica la función func a cada elemento de la matriz. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada.

$A \leftarrow func(B)$

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double).
[in]	B	Matriz a evaluar con func.

Devuelve: true si todo fue bien o false si la matriz era vacia o si no tiene el mismo tamaño que B.

◆ Apply() [5/6]

bool Pds::Matrix::Apply	(	double(*)(double, double)	func,
		double	var
	)

Aplica la función func a cada elemento de la matriz.

$A \leftarrow func(A,var)$

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double,double).
[in]	var	Variable a usar em func(double,var).

Devuelve: true si todo fue bien o false si la matriz era vacia.

◆ Apply() [6/6]

bool Pds::Matrix::Apply	(	double(*)(double, const std::vector< double > &)	func,
		const std::vector< double > &	var
	)

Aplica la función func a cada elemento de la matriz.

$A \leftarrow func(A,var)$

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double,std::vector<double>).
[in]	var	Variable a usar em .

Devuelve: true si todo fue bien o false si la matriz era vacia.

◆ ApplyAdd() [1/2]

bool Pds::Matrix::ApplyAdd	(	double(*)(double)	func,
		double	alpha,
		const Pds::Matrix &	B,
		double	beta,
		const Pds::Matrix &	C
	)

Aplica la función func a cada elemento de la suma ponderada de las matrices. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada.

$A \leftarrow func(\alpha B+\beta C)$

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double double func(double).
[in]	alpha	Factor de B.
[in]	B	Matriz a evaluar con func.
[in]	beta	Factor de C.
[in]	C	Matriz a evaluar con func.

Devuelve: true si todo fue bien o false si la matriz era vacia o si no tiene el mismo tamaño que B.

◆ ApplyAdd() [2/2]

bool Pds::Matrix::ApplyAdd	(	double	alpha,
		const Pds::Matrix &	B,
		double	beta,
		const Pds::Matrix &	C
	)

Aplica la función func a cada elemento de la suma ponderada de las matrices. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada.

$A \leftarrow \alpha B+\beta C$

Parámetros

[in]	alpha	Factor de B.
[in]	B	Matriz a evaluar con func.
[in]	beta	Factor de C.
[in]	C	Matriz a evaluar con func.

Devuelve: true si todo fue bien o false si la matriz era vacia o si no tiene el mismo tamaño que B.

◆ ApplySub() [1/2]

bool Pds::Matrix::ApplySub	(	double(*)(double)	func,
		const Pds::Matrix &	B,
		const Pds::Matrix &	C
	)

Aplica la función func a cada elemento de la diferencia de matrices. La matriz que recibe debe tener el mismo tamaño que a matrices de entrada.

$A \leftarrow func(B-C)$

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double double func(double).
[in]	B	Matriz a evaluar con func.
[in]	C	Matriz a evaluar con func.

Devuelve: true si todo fue bien o false si la matriz era vacia o si no tiene el mismo tamaño que B.

◆ ApplySub() [2/2]

bool Pds::Matrix::ApplySub	(	const Pds::Matrix &	B,
		const Pds::Matrix &	C
	)

Aplica a cada elemento de la diferencia de matrices. La matriz que recibe debe tener el mismo tamaño que las matrices de entrada.

$A \leftarrow B-C$

Parámetros

[in]	B	Matriz a evaluar.
[in]	C	Matriz a evaluar.

Devuelve: true si todo fue bien o false si la matriz era vacia o si no tiene el mismo tamaño que B.

◆ ApplyProduct()

bool Pds::Matrix::ApplyProduct	(	const Pds::Matrix &	B,
		const Pds::Matrix &	C
	)

[Elemento a elemento] Aplica a cada elemento de la multiplicación de matrices. La matriz que recibe debe tener el mismo tamaño que las matrices de entrada.

$A \leftarrow B.C$

Parámetros

[in]	B	Matriz a evaluar.
[in]	C	Matriz a evaluar.

Devuelve: true si todo fue bien o false si la matriz era vacia o si no tiene el mismo tamaño que B.

◆ ApplyInCol() [1/2]

bool Pds::Matrix::ApplyInCol	(	unsigned int	col,
		double(*)(double)	func
	)

Aplica la función func a cada elemento de la columna col de la matriz.

$a_{:col} \leftarrow func(a_{:col})$

Parámetros

[in]	col	Columna a aplicar la función.
[in]	func	Función a aplicar, esta debe tener a forma double func(double).

Devuelve: true si todo fue bien o false si la matriz era vacia.

◆ ApplyInCol() [2/2]

bool Pds::Matrix::ApplyInCol	(	unsigned int	col,
		double(*)(double, double)	func,
		double	var
	)

Aplica la función func a cada elemento de la columna col de la matriz.

$a_{:col} \leftarrow func(a_{:col},var)$

Parámetros

[in]	col	Columna a aplicar la función.
[in]	func	Función a aplicar, esta debe tener a forma double func(double,double).
[in]	var	Variable a usar em func(double,var).

Devuelve: true si todo fue bien o false si la matriz era vacia.

◆ OperateRows() [1/4]

Pds::Matrix Pds::Matrix::OperateRows ( double(*)(const Pds::Matrix &Row) func ) const

Opera la función func usando como entrada cada fila de la matriz.

$\mathbf{X}= \left( \begin{matrix} \mathbf{x}_0^T\\ \mathbf{x}_1^T\\ \vdots\\ \mathbf{x}_l^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) ,\qquad \mathbf{Y}= \left( \begin{matrix} y_0\\ y_1\\ \vdots\\ y_l\\ \vdots\\ y_{L-1}\\ \end{matrix} \right)$

$y_l\leftarrow func(\mathbf{x}_l^T)$

Parámetros

[in] func Función a aplicar, esta debe tener a forma double func(const Pds::Matrix &Row).

Devuelve: Una matriz columna $\mathbf{Y}$ si todo fue bien o una vacia en caso de error.

Ejemplos: example_matrix_operaterows.cpp y example_regression_fitting.cpp.

◆ OperateRows() [2/4]

Pds::Matrix Pds::Matrix::OperateRows ( double(*)(const Pds::Vector &Row) func ) const

Opera la función func usando como entrada cada fila de la matriz.

$\mathbf{X}= \left( \begin{matrix} \mathbf{x}_0^T\\ \mathbf{x}_1^T\\ \vdots\\ \mathbf{x}_l^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) ,\qquad \mathbf{Y}= \left( \begin{matrix} y_0\\ y_1\\ \vdots\\ y_l\\ \vdots\\ y_{L-1}\\ \end{matrix} \right)$

$y_l\leftarrow func(\mathbf{x}_l)$

Parámetros

[in] func Función a aplicar, esta debe tener a forma double func(const Pds::Matrix &Row).

Devuelve: Una matriz columna $\mathbf{Y}$ si todo fue bien o una vacia en caso de error.

◆ OperateRows() [3/4]

Pds::Matrix Pds::Matrix::OperateRows	(	double(*)(const Pds::Vector &Row, const Pds::Vector &C)	func,
		const Pds::Vector &	C
	)		const

Opera la función func usando como entrada cada fila de la matriz.

$\mathbf{X}= \left( \begin{matrix} \mathbf{x}_0^T\\ \mathbf{x}_1^T\\ \vdots\\ \mathbf{x}_l^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) ,\qquad \mathbf{Y}= \left( \begin{matrix} y_0\\ y_1\\ \vdots\\ y_l\\ \vdots\\ y_{L-1}\\ \end{matrix} \right)$

$y_l\leftarrow func(\mathbf{x}_l,C)$

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(const Pds::Matrix &Row).
[in]	C	Vector de parametros.

Devuelve: Una matriz columna $\mathbf{Y}$ si todo fue bien o una vacia en caso de error.

◆ OperateRows() [4/4]

Pds::Matrix Pds::Matrix::OperateRows	(	double(*)(const Pds::Vector &Row, const Pds::Vector &C, const std::vector< double > &var)	func,
		const Pds::Vector &	C,
		const std::vector< double > &	var
	)		const

Opera la función func usando como entrada cada fila de la matriz.

$\mathbf{X}= \left( \begin{matrix} \mathbf{x}_0^T\\ \mathbf{x}_1^T\\ \vdots\\ \mathbf{x}_l^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) ,\qquad \mathbf{Y}= \left( \begin{matrix} y_0\\ y_1\\ \vdots\\ y_l\\ \vdots\\ y_{L-1}\\ \end{matrix} \right)$

$y_l\leftarrow func(\mathbf{x}_l,C,var)$

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(const Pds::Matrix &Row).
[in]	C	Vector auxiliar.
[in]	var	Vector de variables.

Devuelve: Una matriz columna $\mathbf{Y}$ si todo fue bien o una vacia en caso de error.

◆ OperateCols() [1/3]

Pds::Matrix Pds::Matrix::OperateCols ( double(*)(const Pds::Matrix &Col) func ) const

Opera la función func usando como entrada cada columna de la matriz.

$\mathbf{X}= \left( \begin{matrix} \mathbf{x}_0 & \mathbf{x}_1 & \dots & \mathbf{x}_l & \dots & \mathbf{x}_{L-1} \end{matrix} \right) ,\qquad \mathbf{Y}= \left( \begin{matrix} y_0 & y_1 & \dots & y_l & \dots & y_{L-1} \end{matrix} \right)$

$y_l\leftarrow func(\mathbf{x}_l)$

Parámetros

[in] func Función a aplicar, esta debe tener a forma double func(const Pds::Matrix &Col).

Devuelve: Una matriz linea si todo fue bien o una vacia en caso de error.

◆ OperateCols() [2/3]

Pds::Matrix Pds::Matrix::OperateCols ( double(*)(const Pds::Vector &Col) func ) const

Opera la función func usando como entrada cada columna de la matriz.

$\mathbf{X}= \left( \begin{matrix} \mathbf{x}_0 & \mathbf{x}_1 & \dots & \mathbf{x}_l & \dots & \mathbf{x}_{L-1} \end{matrix} \right) ,\qquad \mathbf{Y}= \left( \begin{matrix} y_0 & y_1 & \dots & y_l & \dots & y_{L-1} \end{matrix} \right)$

$y_l\leftarrow func(\mathbf{x}_l)$

Parámetros

[in] func Función a aplicar, esta debe tener a forma double func(const Pds::Matrix &Col).

Devuelve: Una matriz linea si todo fue bien o una vacia en caso de error.

◆ OperateCols() [3/3]

Pds::Matrix Pds::Matrix::OperateCols	(	double(*)(const Pds::Vector &Col, const Pds::Vector &C)	func,
		const Pds::Vector &	C
	)		const

Opera la función func usando como entrada cada columna de la matriz.

$\mathbf{X}= \left( \begin{matrix} \mathbf{x}_0 & \mathbf{x}_1 & \dots & \mathbf{x}_l & \dots & \mathbf{x}_{L-1} \end{matrix} \right) ,\qquad \mathbf{Y}= \left( \begin{matrix} y_0 & y_1 & \dots & y_l & \dots & y_{L-1} \end{matrix} \right)$

$y_l\leftarrow func(\mathbf{x}_l,C)$

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(const Pds::Matrix &Col).
[in]	C	Vector de parámetros.

Devuelve: Una matriz linea si todo fue bien o una vacia en caso de error.

◆ TransformRows()

Pds::Matrix Pds::Matrix::TransformRows	(	Pds::Vector(*)(const Pds::Vector &Row, const Pds::Vector &C)	func,
		const Pds::Vector &	C
	)		const

Opera la función func usando como entrada cada fila de la matriz.

$\mathbf{X}= \left( \begin{matrix} \mathbf{x}_0^T\\ \mathbf{x}_1^T\\ \vdots\\ \mathbf{x}_l^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) ,\qquad \mathbf{Y}= \left( \begin{matrix} y_0^T\\ y_1^T\\ \vdots\\ y_l^T\\ \vdots\\ y_{L-1}^T\\ \end{matrix} \right)$

$y_l\leftarrow func(\mathbf{x}_l,C)$

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma Pds::Vector func(const Pds::Matrix &Row).
[in]	C	Vector de parametros.

Devuelve: Una matriz $\mathbf{Y}$ si todo fue bien o una vacia en caso de error.

◆ Scale()

Pds::Matrix Pds::Matrix::Scale	(	double	minval,
		double	maxval
	)		const

Rescala linearmente los datos desde minval a maxval.

Parámetros

[in]	minval	Valor menor de la escala.
[in]	maxval	Valor maior de la escala.

Devuelve: Retorna la matriz escalada si todo fue bien o una vacia si no.

Ejemplos: example_array_dsp.cpp y example_matrix_export_bmp.cpp.

◆ Round()

Pds::Matrix Pds::Matrix::Round ( unsigned int decimal = 0 ) const

Retorna una matriz con los valores redondeados.

Parámetros

[in] decimal Núros decimales usados.

Devuelve: Retorna la matriz con los valores redondeados si todo fue bien o una vacia si no.

◆ CopyRegion()

bool Pds::Matrix::CopyRegion	(	const Pds::RegionRect &	Rin,
		const Pds::RegionRect &	Rout,
		Pds::Matrix &	Mout
	)		const

Copia la región Rin de la matriz a la región Rout de la matriz Mout.

Ambas regiones deben estar dentro de las matrices y tener el mismo tamaño para que la copia sea realizada.

Parámetros

[in]	Rin	Región en donde se leerán los datos.
[in]	Rout	Región en donde se escribirá.
[out]	Mout	La matriz donde se escribirá.

Devuelve: true si las matrices existen y son copiables o false si no.

◆ InitRegion()

bool Pds::Matrix::InitRegion	(	Pds::RegionRect	R,
		double	val
	)

Inicializa la región R de la matriz con el valor val.

Parámetros

[in]	R	La region a inicializar.
[in]	val	valor a ser usado en la inicialización.

Devuelve: true si todo fue bien o false si no.

Ejemplos: example_matrix_fill.cpp.

◆ GetRegion()

Pds::RegionRect Pds::Matrix::GetRegion ( void ) const

Retorna una variable Pds::RegionRect desde la posicion (0,0), con ancho y alto (Mat.Nlin(),Mat.Ncol()).

Devuelve: La region si todo fue bien, sino se retorna una region donde IsEmpty() == true.

◆ MeanOfRegion() [1/2]

bool Pds::Matrix::MeanOfRegion	(	const Pds::RegionRect &	Rin,
		double *	mean
	)		const

Calcula la media de los elementos en la region, pero para que sea calculado debe existir una interseccion diferente de zero con la matriz. Los valores fuera de la matriz son considerados cero.

$R=Rin\cap R_{A}$

$mean=\mu_{R}= \frac{\sum \limits_{i\in R} Mat\{i\}}{card(R)}$

Parámetros

[in]	Rin	La region a calcular.
[out]	mean	Media.

Devuelve: true si todo fue bien o false si no (ej: mean==NULL).

◆ MeanOfRegion() [2/2]

double Pds::Matrix::MeanOfRegion ( const Pds::RegionRect & Rin ) const

Calcula la media de los elementos en la region, pero para que sea calculado debe existir una interseccion diferente de zero con la matriz. Los valores fuera de la matriz son considerados cero.

$R=Rin\cap R_{A}$

$mean=\mu_{R}= \frac{\sum \limits_{i\in R} Mat\{i\}}{card(R)}$

Parámetros

[in] Rin La region a calcular.

Devuelve: la media o Pds::Ra::Nan si hubo un error (ej: IsEmpty()==true).

◆ MeanSquareOfRegion() [1/2]

bool Pds::Matrix::MeanSquareOfRegion	(	const Pds::RegionRect &	Rin,
		double *	mean
	)		const

Calcula la media del cuadrado de los elementos en la region, pero para que sea calculado debe existir una interseccion diferente de zero con la matriz. Los valores fuera de la matriz son considerados cero.

$R=Rin\cap R_{A}$

$mean=\mu_{R}= \frac{\sum \limits_{i\in R} Mat\{i\}^2}{card(R)}$

Parámetros

[in]	Rin	La region a calcular.
[out]	mean	Media.

Devuelve: true si todo fue bien o false si no (ej: mean==NULL).

◆ MeanSquareOfRegion() [2/2]

double Pds::Matrix::MeanSquareOfRegion ( const Pds::RegionRect & Rin ) const

Calcula la media del cuadrado de los elementos en la region, pero para que sea calculado debe existir una interseccion diferente de zero con la matriz. Los valores fuera de la matriz son considerados cero.

$R=Rin\cap R_{A}$

$mean=\mu_{R}= \frac{\sum \limits_{i\in R} Mat\{i\}^2}{card(R)}$

Parámetros

[in] Rin La region a calcular.

Devuelve: la media o Pds::Ra::Nan si hubo un error (ej: IsEmpty()==true).

◆ StdAndMeanOfRegion()

bool Pds::Matrix::StdAndMeanOfRegion	(	const Pds::RegionRect &	Rin,
		double *	std,
		double *	mean
	)		const

Calcula el desvío padrón y la media de los elementos de la intersección de la región con la matriz.

$R=Rin\cap R_{A}$

$mean=\mu_{R}= \frac{\sum \limits_{i\in R} Mat\{i\}}{card(R)}, \quad std=\sigma_{R}= \sqrt{\frac{\sum \limits_{i\in R} \left(Mat\{i\}-\mu_{R}\right)^2}{card(R)}}$

Parámetros

[in]	Rin	La región a calcular.
[out]	std	Desvío padrón.
[out]	mean	Media.

Devuelve: true si todo fue bien o false si no (ej: IsEmpty()==true).

◆ CorrNormRegions() [1/2]

bool Pds::Matrix::CorrNormRegions	(	const Pds::Matrix &	M1,
		const Pds::RegionRect &	R0,
		const Pds::RegionRect &	R1,
		double *	corrn
	)		const

Calcula correlación normalizada entre los elementos de la intersección de la regiones con sus matrices.

Para que la correlacion sea ejecutada se debe cumplir que ademas que $R_0 \subset M_0$ y $R_1 \subset M_1$ . Con estas condiciones obtenemos las submatrices y .

$S_0 \equiv {M_0}_{R_0}, \qquad S_1 \equiv {M_1}_{R_1}$

$CORR=\frac{E[S_0~S_1]}{\sqrt{MS\{S_0\}~MS\{S_1\}}}$

Parámetros

[in]	M1	Una matriz de la correlación.
[in]	R0	La región a analizar en la matriz M0, el tamaño de R0 debe ser igual al tamaño de R1.
[in]	R1	La región a analizar en la matriz M1, el tamaño de R0 debe ser igual al tamaño de R1.
[out]	corrn	Correlación normalizada.

Devuelve: true si todo fue bien o false si no (ej: pcc==NULL). Retorna false cuando algún lado de las regiones a analizar son cero.

◆ CorrNormRegions() [2/2]

bool Pds::Matrix::CorrNormRegions	(	const Pds::Matrix &	M1,
		const Pds::RegionRect &	R0,
		const Pds::RegionRect &	R1,
		double	means0,
		double	means1,
		double *	corrn
	)		const

Calcula correlación normalizada entre los elementos de la intersección de la regiones con sus matrices.

Para que la correlacion sea ejecutada se debe cumplir que ademas que $R_0 \subset M_0$ y $R_1 \subset M_1$ . Con estas condiciones obtenemos las submatrices y .

$S_0 \equiv {M_0}_{R_0}, \qquad S_1 \equiv {M_1}_{R_1}$

$CORR=\frac{E[S_0~S_1]}{\sqrt{MS\{S_0\}~MS\{S_1\}}}$

Parámetros

[in]	M1	Una matriz de la correlación.
[in]	R0	La región a analizar en la matriz M0, el tamaño de R0 debe ser igual al tamaño de R1.
[in]	R1	La región a analizar en la matriz M1, el tamaño de R0 debe ser igual al tamaño de R1.
[in]	means0	Valor cuadrático medio de la region R0, $MS\{S_0\}$ .
[in]	means1	Valor cuadrático medio de la region R1, $MS\{S_1\}$ .
[out]	corrn	Correlación normalizada.

Devuelve: true si todo fue bien o false si no (ej: pcc==NULL). Retorna false cuando algún lado de las regiones a analizar son cero.

◆ CorrPearsonRegions() [1/2]

bool Pds::Matrix::CorrPearsonRegions	(	const Pds::Matrix &	M1,
		const Pds::RegionRect &	R0,
		const Pds::RegionRect &	R1,
		double *	pcc
	)		const

Calcula el coeficiente de correlación de Pearson (PCC) entre los elementos de la intersección de la regiones con sus matrices.

Para que la correlacion sea ejecutada se debe cumplir que ademas que $R_0 \subset M_0$ y $R_1 \subset M_1$ . Con estas condiciones obtenemos las submatrices y .

$S_0 \equiv {M_0}_{R_0}, \qquad S_1 \equiv {M_1}_{R_1}$

$PCC=\frac{E[(S_0-\mu_{S_0})(S_1-\mu_{S_1})]}{\sigma_{S_0}\sigma_{S_1}}$

Si algun desvío padrón es cero entonces existen casos especiales para el valor de PCC.

Casos especiales para PCC
PCC	sigma0	sigma1	mean0	mean1
0.0	Zero	NonZero	?	?
0.0	NonZero	Zero	?	?
1.0	Zero	Zero	Positive	Positive
1.0	Zero	Zero	Negative	Negative
-1.0	Zero	Zero	Positive	Negative
-1.0	Zero	Zero	Negative	Positive
0.0	Zero	Zero	Zero	NonZero
0.0	Zero	Zero	NonZero	Zero
1.0	Zero	Zero	Zero	Zero

Parámetros

[in]	M1	Una matriz de la correlación.
[in]	R0	La región a analizar en la matriz M0, el tamaño de R0 debe ser igual al tamaño de R1.
[in]	R1	La región a analizar en la matriz M1, el tamaño de R0 debe ser igual al tamaño de R1.
[out]	pcc	Coeficiente de correlación de Pearson.

Devuelve: true si todo fue bien o false si no (ej: pcc==NULL). Retorna false cuando algún lado de las regiones a analizar son cero.

◆ CorrPearsonRegions() [2/2]

bool Pds::Matrix::CorrPearsonRegions	(	const Pds::Matrix &	M1,
		const Pds::RegionRect &	R0,
		const Pds::RegionRect &	R1,
		double	mean0,
		double	mean1,
		double	std0,
		double	std1,
		double *	pcc
	)		const

Calcula el coeficiente de correlación de Pearson (PCC) entre los elementos de la intersección de la regiones con sus matrices.

Para que la correlacion sea ejecutada se debe cumplir que ademas que $R_0 \subset M_0$ y $R_1 \subset M_1$ . Con estas condiciones obtenemos las submatrices y .

$S_0 \equiv {M_0}_{R_0}, \qquad S_1 \equiv {M_1}_{R_1}$

$PCC=\frac{E[(S_0-\mu_{S_0})(S_1-\mu_{S_1})]}{\sigma_{S_0}\sigma_{S_1}}$

Si algun desvío padrón es cero entonces existen casos especiales para el valor de PCC.

Casos especiales para PCC
PCC	sigma0	sigma1	mean0	mean1
0.0	Zero	NonZero	?	?
0.0	NonZero	Zero	?	?
1.0	Zero	Zero	Positive	Positive
1.0	Zero	Zero	Negative	Negative
-1.0	Zero	Zero	Positive	Negative
-1.0	Zero	Zero	Negative	Positive
0.0	Zero	Zero	Zero	NonZero
0.0	Zero	Zero	NonZero	Zero
1.0	Zero	Zero	Zero	Zero

Parámetros

[in]	M1	Una matriz de la correlación.
[in]	R0	La región a analizar en la matriz M0, el tamaño de R0 debe ser igual al tamaño de R1.
[in]	R1	La región a analizar en la matriz M1, el tamaño de R0 debe ser igual al tamaño de R1.
[in]	mean0	La media de la region R0.
[in]	mean1	La media de la region R1.
[in]	std0	El desvio padron de la region R0.
[in]	std1	El desvio padron de la region R1.
[out]	pcc	Coeficiente de correlación de Pearson.

Devuelve: true si todo fue bien o false si no (ej: pcc==NULL). Retorna false cuando algún lado de las regiones a analizar son cero.

◆ ToString() [1/2]

std::string Pds::Matrix::ToString ( void ) const

Convierte los datos de la matriz en un std::string.

Devuelve: Retorna un std::string. Si la matriz es nula retorna un string sin caracteres.

Ejemplos: example_binarytreenode.cpp y example_vector_create.cpp.

◆ ToString() [2/2]

std::string Pds::Matrix::ToString ( const std::string & EndData ) const

Convierte los datos de la matriz en un std::string.

Parámetros

[in] EndData Texto a mostrar al final del todo, se recomienda "\n".

Devuelve: Retorna un std::string. Si la matriz es nula retorna un string sin caracteres.

◆ Print() [1/3]

void Pds::Matrix::Print	(	const std::string &	str,
		unsigned int	precision
	)		const

Imprime en pantalla el contenido de la matriz después del texto indicado en str.

Parámetros

[in]	str	Texto a mostrar antes de imprimir.
[in]	precision	Cantidad maxima de números a ser mostrados al imprimir.

Ejemplos: example_array_create.cpp, example_array_dsp.cpp, example_circle_create.cpp, example_csv_create.cpp, example_funcconvexhull_incremental.cpp, example_funcconvexhull_isinside.cpp, example_funcmatrix_indexsum.cpp, example_funcmatrix_merge.cpp, example_funcvector_space.cpp, example_matrix_algebra.cpp, example_matrix_algebra3.cpp, example_matrix_algebra4.cpp, example_matrix_algebra_cholesky.cpp, example_matrix_algebra_eig.cpp, example_matrix_algebra_eig2.cpp, example_matrix_assignment.cpp, example_matrix_assignment_bin.cpp, example_matrix_create.cpp, example_matrix_dsp.cpp, example_matrix_dsp2.cpp, example_matrix_dsp_conv.cpp, example_matrix_dsp_conv2d.cpp, example_matrix_dsp_hist.cpp, example_matrix_export.cpp, example_matrix_fill.cpp, example_matrix_fill_rv.cpp, example_matrix_getset.cpp, example_matrix_getset_extras.cpp, example_matrix_json.cpp, example_matrix_knearest.cpp, example_matrix_operaterows.cpp, example_matrix_operator_binario_bin.cpp, example_matrix_operator_unario.cpp, example_matrix_operators_binary.cpp, example_matrix_operators_binary2.cpp, example_matrix_sampleblock.cpp, example_matrix_save_load.cpp, example_matrix_static_matrix.cpp, example_matrixfunc.cpp, example_matrixfunc_meshgrid.cpp, example_matrixmath.cpp, example_matrixmath_dsp.cpp, example_matrixmath_erf.cpp, example_matrixrotation.cpp, example_octave_show.cpp, example_optadam_create.cpp, example_ra_indices.cpp, example_regression_fitting.cpp, example_vector_create.cpp, example_vector_dsp.cpp, example_vector_dsp_conv.cpp, example_vector_dsp_conv1d.cpp, example_vector_export_json.cpp, example_vector_json.cpp, example_vector_nearestk.cpp, example_vector_operator_unit.cpp, example_vector_poly.cpp, example_vector_sorting.cpp y example_vectorfunc.cpp.

◆ Print() [2/3]

void Pds::Matrix::Print ( const std::string & str ) const

Imprime en pantalla el contenido de la matriz después del texto indicado en str.

Parámetros

[in] str Texto a mostrar antes de imprimir.

◆ Print() [3/3]

void Pds::Matrix::Print ( void ) const

Imprime en pantalla el contenido de la matriz.

◆ MakeEmpty()

void Pds::Matrix::MakeEmpty ( void )

libera los datos internos de la matriz y la convierte en una matriz nula. es decir con lineas y columnas cero.

Una matriz $\mathbf{A}$ está vacía si $\mathbf{A}=[]_{0,0}$ .

Ejemplos: example_matrix_export.cpp y example_matrixfunc.cpp.

◆ Reshape()

bool Pds::Matrix::Reshape	(	unsigned int	Nlin,
		unsigned int	Ncol
	)

Remodela los datos internos de la array y la convierte en una array de tamaño diferente, los datos que faltan se rellenan con cero.

Parámetros

[in]	Nlin	Número de lineas. Da error si el valor es cero.
[in]	Ncol	Número de columnas. Da error si el valor es cero.

Devuelve: Retorna true si todo fue bien o false si no.

◆ Remodel()

Pds::Matrix Pds::Matrix::Remodel	(	unsigned int	Nlin,
		unsigned int	Ncol
	)

Remodela los datos internos de la array y retorna un array de tamaño diferente, los datos que faltan se rellenan con cero.

Parámetros

[in]	Nlin	Número de lineas. Da error si el valor es cero.
[in]	Ncol	Número de columnas. Da error si el valor es cero.

Devuelve: Retorna una matriz con el nuevo tamaño.

◆ FusionVer()

bool Pds::Matrix::FusionVer ( std::list< Pds::Matrix > & list )

Concatena verticalmente varias matrices.
Si las matrices no tienen el mismo número de columnas se considera um error. Destruye las matrices en list. Este metodo es mas rapido que Pds::MergeVer(list) pues transplanta memoria.

Parámetros

[in] list La lista de matrices a concatenar.

Devuelve: Retorna true en caso de enxito en la matriz concatenada o false y una matriz vacía en caso de error.

Ejemplos: example_matrixfunc.cpp.

◆ SaveInStream()

bool Pds::Matrix::SaveInStream ( std::ofstream & myfile ) const

Escribe en un archivo de texto el contenido de la matriz.

Por exemplo si guardamos una matriz A=Pds::Eye(3) entonces se escribirá:

     0       0
     1       0
     0       1

Donde cada elemento es separado por tabuladores y cada linea por un salto de linea. Este formato de almacenamiento de datos puede ser leido usando LoadFromStream() o Load(), tambien puede ser leido linea a linea usando LoadLineFromStream().

Parámetros

[in] myfile Stream del archivo donde se escribirán los datos.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_save_load.cpp.

◆ LoadFromStream()

bool Pds::Matrix::LoadFromStream	(	std::ifstream &	ifs,
		unsigned int	Nlin,
		unsigned int	Ncol
	)

Lee Nlin*Ncol elementos desde un archivo, estos elementos son colocados en una matriz de Nlin lineas y Ncol columnas. Cada elemento es separado por tabuladores y cada linea por un salto de linea.

Si la lectura es satisfactoria el contenido actual de la matriz es liberado y un nuevo espacio de memoria es separado, en caso de error la matriz queda vacia, es decir IsEmpty() retorna true.

Por exemplo si tenemos un archivo filedat.txt con el texto:

     0       0
     1       0
     0       1

Podremos leer el contenido desde la posición de ifs (inicio) y cargar la matriz A usando:

A.LoadFromStream(ifs,3,3); // Matrix of 3x3.

o

A.LoadFromStream(ifs,1,9); // Matrix of 1x9.

Este formato de almacenamiento de datos proviene de usar SaveInStream() o Save().

Parámetros

[in]	ifs	Stream del archivo donde se leerán los datos.
[in]	Nlin	El número de lineas en el arreglo.
[in]	Ncol	El número de columnas en el arreglo.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_save_load.cpp.

◆ LoadLineFromStream()

bool Pds::Matrix::LoadLineFromStream ( std::ifstream & ifs )

Lee una linea de un archivo y crea una matriz de Nlin=1 y Ncol columnas. Cada elemento es separado por tabuladores y cada linea por un salto de linea.

Si la lectura es satisfactoria el contenido actual de la matriz es liberado y un nuevo espacio de memoria es separado, en caso de error la matriz queda vacia, es decir IsEmpty() retorna true.

Por exemplo si tenemos un archivo filedat.txt con el texto:

     2       -1
     1       0       1       0
     0       1       -1

Podremos leer el contenido desde la posición de ifs (inicio) y cargar la matriz A usando:

A.LoadLineFromStream(ifs); // The matrix A has 1x3 size.

Este formato de almacenamiento de datos proviene de usar SaveInStream() o Save().

Parámetros

[in] ifs Stream del archivo donde se leerán los datos.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_save_load.cpp.

◆ Save()

bool Pds::Matrix::Save ( const std::string & filepath ) const

Escribe en un archivo de texto el contenido de la matriz.

Por exemplo si guardamos una matriz A=Pds::Eye(3) entonces se escribirá:

     0       0
     1       0
     0       1

Donde cada elemento es separado por tabuladores y cada linea por un salto de linea. Este formato de almacenamiento de datos puede ser leido usando LoadFromStream() o Load(), tambien puede ser leido linea a linea usando LoadLineFromStream().

Parámetros

[in] filepath El archivo donde se escribirán los datos.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_create.cpp, example_matrix_export.cpp, example_matrix_save_load.cpp, example_matrix_static_matrix.cpp y example_ra_string.cpp.

◆ Load()

bool Pds::Matrix::Load ( const std::string & filepath )

Lee desde un archivo una matriz de Nlin lineas y Ncol columnas.

Si la lectura es satisfactoria el contenido actual de la matriz es liberado y un nuevo espacio de memoria es separado, en caso de error la matriz queda vacia, es decir IsEmpty() retorna true.

Por exemplo si tenemos un archivo filedat.txt con el texto:

     0       0
     1       0
     0       1

Podremos leer el contenido y cargar la matriz A usando:

A.LoadFromStream("filedat.txt"); // Matrix of 3x3.

La cantidad de lineas y columnas es automaticamente detectada. Para que la lecture sea considerada satisfactoria, todas las lineas deben tener la misma cantidad de elementos.

Este formato de almacenamiento de datos proviene de usar SaveInStream() o Save().

Parámetros

[in] filepath El archivo donde se leerán los datos.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_algebra_eig2.cpp y example_matrix_static_matrix.cpp.

◆ ExportCsvFile() [1/2]

bool Pds::Matrix::ExportCsvFile	(	const std::string &	filepath,
		char	delimitador = `','`
	)		const

Escribe en un archivo de texto el contenido de la matriz usando un formato Csv (Comma Separated Values).

Las columnas son etiquetadas (tituladas) con COL0,COL1,... Por exemplo si guardamos una matriz A=Pds::Eye(3) usando A.ExportCsvFile("filedat.csv") entonces se escribirá:

COL0,COL1,COL2
1,0,0
0,1,0
0,0,1

Donde cada elemento es separado por una coma y cada linea por un salto de linea. Este formato de almacenamiento de datos puede ser leido usando ImportCsvFile().

Parámetros

[in]	filepath	El archivo donde se escribirán los datos.
[in]	delimitador	Delimitador separador de elementos, ',' por defecto.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_export.cpp.

◆ ExportCsvFile() [2/2]

bool Pds::Matrix::ExportCsvFile	(	const std::string &	filepath,
		std::vector< std::string >	titles,
		char	delimitador = `','`
	)		const

Escribe en un archivo de texto el contenido de la matriz usando un formato Csv (Comma Separated Values).

Por exemplo si guardamos una matriz A=Pds::Eye(3) usando A.ExportCsvFile("filedat.csv",{"Dog","Bird","Cat"}) entonces se escribirá:

Dog,Bird,Cat
1,0,0
0,1,0
0,0,1

Donde cada elemento es separado por una coma y cada linea por un salto de linea. Este formato de almacenamiento de datos puede ser leido usando ImportCsvFile().

Parámetros

[in]	filepath	El archivo donde se escribirán los datos.
[in]	titles	Titulos al inicio del archivo. Solo se crea el archivo Csv si el número de elementos es igual a Ncol.
[in]	delimitador	Delimitador separador de elementos, ',' por defecto.

Devuelve: Retorna true si todo fue bien o false en caso de error.

◆ ImportCsvFile()

bool Pds::Matrix::ImportCsvFile	(	const std::string &	filepath,
		char	delimitador,
		std::vector< std::string > &	titles
	)

Lee un archivo de texto el contenido de la matriz usando un formato Csv (Comma Separated Values).

Si la lectura es satisfactoria el contenido actual de la matriz es liberado y un nuevo espacio de memoria es separado, en caso de error la matriz queda vacia, es decir IsEmpty() retorna true.

Por exemplo si tenemos un archivo filedat.csv con el texto:

Dog,Bird,Cat
1,0,0
0,1,0
0,0,1

Podremos leer el contenido y cargar la matriz A usando:

A.ImportCsvFile("filedat.csv",',',titles);

La cantidad de lineas y columnas es automaticamente detectada. Para que la lecture sea considerada satisfactoria, todas las lineas deben tener la misma cantidad de elementos.

Este formato de almacenamiento de datos proviene de usar SaveInStream() o Save().

Parámetros

[in]	filepath	El archivo donde se leerán los datos.
[in]	delimitador	Delimitador separador de elementos, ',' por defecto.
[in]	titles	Titulos al inicio del archivo.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_export.cpp.

◆ ImportCsvFileWithoutTitles()

bool Pds::Matrix::ImportCsvFileWithoutTitles	(	const std::string &	filepath,
		char	delimitador
	)

Lee un archivo de texto el contenido de la matriz usando un formato Csv (Comma Separated Values).

Si la lectura es satisfactoria el contenido actual de la matriz es liberado y un nuevo espacio de memoria es separado, en caso de error la matriz queda vacia, es decir IsEmpty() retorna true.

Por exemplo si tenemos un archivo filedat.csv con el texto:

1,0,0
0,1,0
0,0,1

Podremos leer el contenido y cargar la matriz A usando:

A.ImportCsvFile("filedat.csv",',');

La cantidad de lineas y columnas es automaticamente detectada. Para que la lecture sea considerada satisfactoria, todas las lineas deben tener la misma cantidad de elementos.

Este formato de almacenamiento de datos proviene de usar SaveInStream() o Save().

Parámetros

[in]	filepath	El archivo donde se leerán los datos.
[in]	delimitador	Delimitador separador de elementos, ',' por defecto.

Devuelve: Retorna true si todo fue bien o false en caso de error.

◆ ExportTexFile() [1/3]

bool Pds::Matrix::ExportTexFile	(	const std::string &	filepath,
		const std::vector< std::string > &	titles,
		const std::vector< std::string > &	rowtitles,
		const std::string &	caption = `"My caption"`,
		const std::string &	label = `"mylabel"`
	)		const

Escribe en un archivo de texto el contenido de la matriz usando un formato de tabla de tex.

Por exemplo si guardamos una matriz A=Pds::Eye(3) usando A.ExportTexFile("filedat.tex",{"Dog","Bird","Cat"},{"A","B","C"}) entonces se escribirá:

\begin{table}[h!]
\centering
 \begin{tabular}{||c c c ||} 
 \hline
Dog & Bird & Cat \\ [0.5ex] 
 \hline\hline
1 & 0 & 0\\ 
0 & 1 & 0\\ 
0 & 0 & 1\\ 
 [1ex]\hline
 \end{tabular}
 \caption{Table of matrix 0x563dc030a740}
 \label{table:0x563dc030a740}
\end{table}

Parámetros

[in]	filepath	El archivo donde se escribirán los datos.
[in]	titles	Titulos al inicio de la tabla. Solo se crea el archivo tex si el número de elementos es igual a Ncol.
[in]	rowtitles	Titulos al inicio de cada fila. Solo se crea el archivo tex si el número de elementos es igual a Nlin.
[in]	caption	Caption en la tabla.
[in]	label	Etiqueta en la tabla.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_export.cpp.

◆ ExportTexFile() [2/3]

bool Pds::Matrix::ExportTexFile	(	const std::string &	filepath,
		const std::vector< std::string > &	titles,
		const std::string &	caption = `"My caption"`,
		const std::string &	label = `"mylabel"`
	)		const

Escribe en un archivo de texto el contenido de la matriz usando un formato de tabla de tex.

Por exemplo si guardamos una matriz A=Pds::Eye(3) usando A.ExportTexFile("filedat.tex",{"Dog","Bird","Cat"}) entonces se escribirá:

\begin{table}[h!]
\centering
 \begin{tabular}{||c c c ||} 
 \hline
Dog & Bird & Cat \\ [0.5ex] 
 \hline\hline
1 & 0 & 0\\ 
0 & 1 & 0\\ 
0 & 0 & 1\\ 
 [1ex]\hline
 \end{tabular}
 \caption{Table of matrix 0x563dc030a740}
 \label{table:0x563dc030a740}
\end{table}

Parámetros

[in]	filepath	El archivo donde se escribirán los datos.
[in]	titles	Titulos al inicio de la tabla. Solo se crea el archivo tex si el número de elementos es igual a Ncol.
[in]	caption	Caption en la tabla.
[in]	label	Etiqueta en la tabla.

Devuelve: Retorna true si todo fue bien o false en caso de error.

◆ ExportTexFile() [3/3]

bool Pds::Matrix::ExportTexFile	(	const std::string &	filepath,
		const std::string &	caption = `"My caption"`,
		const std::string &	label = `"mylabel"`
	)		const

Escribe en un archivo de texto el contenido de la matriz usando un formato de tabla de tex.

Las columnas son etiquetadas (tituladas) con COL0,COL1,... Por exemplo si guardamos una matriz A=Pds::Eye(3) usando A.ExportTexFile("filedat.tex") entonces se escribirá:

\begin{table}[h!]
\centering
 \begin{tabular}{||c c c ||} 
 \hline
COL0 & COL1 & COL2 \\ [0.5ex] 
 \hline\hline
1 & 0 & 0\\ 
0 & 1 & 0\\ 
0 & 0 & 1\\ 
 [1ex]\hline
 \end{tabular}
 \caption{Table of matrix 0x563dc030a740}
 \label{table:0x563dc030a740}
\end{table}

Parámetros

[in]	filepath	El archivo donde se escribirán los datos. Solo se crea el archivo tex si el número de elementos es igual a Ncol.
[in]	caption	Caption en la tabla.
[in]	label	Etiqueta en la tabla.

Devuelve: Retorna true si todo fue bien o false en caso de error.

◆ ExportJsonToStream() [1/2]

bool Pds::Matrix::ExportJsonToStream ( std::ofstream & myfile ) const

Escribe en un archivo Json el contenido de la matriz.

Por exemplo si guardamos una matriz A.FillId() entonces se escribirá:

{
        "Matrix":
        {
                "Nlin":2,
                "Ncol":3,
                "Array":[0, 1, 2, 3, 4, 5 ]
        }
}

Este formato de almacenamiento de datos puede ser leido usando ImportJsonFromStream().

Parámetros

[in] myfile Stream del archivo donde se escribirán los datos.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_export_json.cpp.

◆ ExportJsonToStream() [2/2]

bool Pds::Matrix::ExportJsonToStream	(	std::ofstream &	myfile,
		unsigned int	ntabs
	)		const

Escribe en un archivo Json el contenido de la matriz.

Por exemplo si guardamos una matriz A.FillId() entonces se escribirá:

{
     "Matrix":
     {
             "Nlin":2,
             "Ncol":3,
             "Array":[0, 1, 2, 3, 4, 5 ]
     }
}

Este formato de almacenamiento de datos puede ser leido usando ImportJsonFromStream().

Parámetros

[in]	myfile	Stream del archivo donde se escribirán los datos.
[in]	ntabs	Número de tabs antes de cada linea.

Devuelve: Retorna true si todo fue bien o false en caso de error.

◆ ExportJsonToString()

std::string Pds::Matrix::ExportJsonToString ( unsigned int ntabs ) const

Retorna una cadena de texto en formato Json con el contenido de la matriz.

Por exemplo si guardamos una matriz A.FillId() entonces se retornará:

{
     "Matrix":
     {
             "Nlin":2,
             "Ncol":3,
             "Array":[0, 1, 2, 3, 4, 5 ]
     }
}

Este formato de almacenamiento de datos puede ser leido usando ImportJsonFromString().

Parámetros

[in] ntabs Número de tabs antes de cada linea.

Devuelve: Retorna una cadena de texto en formato Json con el contenido de la matriz.

Ejemplos: example_matrix_export_json.cpp.

◆ ToJson()

Pds::Json Pds::Matrix::ToJson ( void ) const

Retorna un objeto Pds::Json con el contenido de la matriz.

Por exemplo si guardamos una matriz A.FillId() entonces se retornará:

{
     "Matrix":
     {
             "Nlin":2,
             "Ncol":3,
             "Array":[0, 1, 2, 3, 4, 5 ]
     }
}

Devuelve: Retorna un objeto Pds::Json con el contenido de la matriz.

Ejemplos: example_matrix_json.cpp.

◆ FromJson()

bool Pds::Matrix::FromJson ( const Pds::Json & J )

Lee un objeto Pds::Json busca la etiqueta "Matrix" y lo carga en la matriz. El objeto debe tener al menos los siguientes dados.

{
     "Matrix":
     {
             "Nlin":2,
             "Ncol":3,
             "Array":[0, 1, 2, 3, 4, 5 ]
     }
}

Donde Nlin*Ncol = size(Array).

Devuelve: Retorna true si la lectura sucedió sin errores y false si no. Si la lectura es incorrecta la matriz se vuelve vacia.

Ejemplos: example_matrix_json.cpp.

◆ ExportXmlToStream()

bool Pds::Matrix::ExportXmlToStream ( std::ofstream & myfile ) const

Escribe en un archivo Xml el contenido de la matriz.

Por exemplo si guardamos una matriz A=Pds::Eye(3) entonces se escribirá:

<Pds::Matrix>
<Nlin>3</Nlin>
<Ncol>3</Ncol>
<Array>
1       0       0
0       1       0
0       0       1
</Array>
</Pds::Matrix>

Este formato de almacenamiento de datos puede ser leido usando ImportXmlFromStream().

Parámetros

[in] myfile Stream del archivo donde se escribirán los datos.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_export.cpp.

◆ ExportXmlToStringStream()

bool Pds::Matrix::ExportXmlToStringStream ( std::stringstream & sstream ) const

Escribe en un std::stringstream en formato Xml el contenido de la matriz.

Por exemplo si guardamos una matriz A=Pds::Eye(3) entonces se escribirá:

<Pds::Matrix>
<Nlin>3</Nlin>
<Ncol>3</Ncol>
<Array>
1       0       0
0       1       0
0       0       1
</Array>
</Pds::Matrix>

Parámetros

[in] sstream Stream donde se escribirán los datos.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_export.cpp.

◆ ExportXmlToString()

std::string Pds::Matrix::ExportXmlToString ( void ) const

Retorna un std::string en formato Xml con el contenido de la matriz.

Por exemplo si guardamos una matriz A=Pds::Eye(3) entonces en el std::string se escribirá:

<Pds::Matrix>
<Nlin>3</Nlin>
<Ncol>3</Ncol>
<Array>
1       0       0
0       1       0
0       0       1
</Array>
</Pds::Matrix>

Devuelve: Retorna un std::string en formato Xml con el contenido de la matriz.

Ejemplos: example_matrix_export.cpp.

◆ ImportXmlFromString()

bool Pds::Matrix::ImportXmlFromString ( const std::string & str )

Carga el contenido de una matriz desde un std::string en formato Xml.

Si la lectura es satisfactoria el contenido actual de la matriz es liberado y un nuevo espacio de memoria es separado, en caso de error la matriz queda vacia, es decir IsEmpty() retorna true.

Por exemplo si tenemos un std::string str con el texto:

<Pds::Matrix>
<Nlin>3</Nlin>
<Ncol>3</Ncol>
<Array>
1       0       0
0       1       0
0       0       1
</Array>
</Pds::Matrix>

Podremos leer el contenido y cargar la matriz A usando:

A.ImportXmlFromString(str);

Para que la lecture sea considerada satisfactoria, la cantidad de elementos del Array debe ser igual a Nlin*Ncol, Nlin y Ncol deben ser diferentes de cero.

Este formato de almacenamiento de datos proviene de usar ExportXmlToString().

Parámetros

[in] str El std::string donde se leerán los datos.

Devuelve: Retorna true si todo fue bien o false en caso de error.

Ejemplos: example_matrix_export.cpp.

◆ ExportMatFile()

bool Pds::Matrix::ExportMatFile	(	const std::string &	pname,
		const std::string &	filepath
	)		const

Escribe en un archivo binario en formato de octave la matriz. Es necesario dar un nombre como identificador de matriz.

Por ejemplo podemos usar el siguiente código para exportar la matriz B:

B.ExportMatFile("B","matfile.mat");

Para cargar todos los datos en OCTAVE se puede usar el siguiente código

% Load all the variables in "matfile.mat" in the workspace.

load("-v4","matfile.mat");

o para cargar la matriz B en una estructura.

% Load the B variable in a STRUCTURE

STRUCTURE=load("-v4","matfile.mat","B");

Version 4 MAT-File Format:Documento externo Documento oficial

Parámetros

[in]	pname	El nombre de la matriz.
[in]	filepath	El archivo donde se escribirán los datos.

Devuelve: Retorna true si todo fue bien o false si no.

Ejemplos: example_matrix_export.cpp.

◆ ExportOctaveString()

std::string Pds::Matrix::ExportOctaveString ( const std::string & pname ) const

Retorna un std:string con los datos de la matriz en el formato de octave. Es necesario dar un nombre como identificador de matriz.

Por ejemplo podemos usar el siguiente código para exportar la matriz B:


std::cout<<B.ExportOctaveString("Bmat");

La salida sería:

     Elapsed time: 3.14159 s

Parámetros

[in] pname El nombre de la matriz.

Devuelve: Retorna un std:string con los datos de la matriz en el formato de octave.

Ejemplos: example_matrix_export.cpp.

◆ ExportBmpFile() [1/2]

bool Pds::Matrix::ExportBmpFile	(	const unsigned char	colormap[256][3],
		const std::string &	filepath
	)		const

Escribe en una matriz en un archivo binario en formato BMP. Losdatos deben ir de 0 a 255, valores superiores o inferiores serán truncados.

A.ExportBmpFile(Pds::Colormap::Jet,"image.bmp");

image.bmp

Parámetros

[in]	colormap	Mapa de colores. Ejemplo: Pds::Colormap::Jet, Pds::Colormap::Bone, Pds::Colormap::Hot,Pds::Colormap::Jolly.
[in]	filepath	Nombre del archivo donde se escribirán los datos

Devuelve: Retorna true si todo fue bien o false si no.

Ejemplos: example_matrix_export_bmp.cpp y example_matrix_fill.cpp.

◆ ExportBmpFileScale()

bool Pds::Matrix::ExportBmpFileScale	(	const unsigned char	colormap[256][3],
		const std::string &	filepath
	)		const

Escribe en una matriz en un archivo binario en formato BMP. Escala los datos de de 0 a 255, si el valor minimo y máximo son iguales la matriz se llena con ceros.

A.ExportBmpFileScale(Pds::Colormap::Jet,"image.bmp");

image.bmp

Parámetros

[in]	colormap	Mapa de colores. Ejemplo: Pds::Colormap::Jet, Pds::Colormap::Bone, Pds::Colormap::Hot,Pds::Colormap::Jolly.
[in]	filepath	Nombre del archivo donde se escribirán los datos

Devuelve: Retorna true si todo fue bien o false si no.

◆ FunctionCh3ToCh3()

static bool Pds::Matrix::FunctionCh3ToCh3	(	void(*)(double a1, double a2, double a3, double &b1, double &b2, double &b3)	func,
		const Pds::Matrix &	A1,
		const Pds::Matrix &	A2,
		const Pds::Matrix &	A3,
		Pds::Matrix &	B1,
		Pds::Matrix &	B2,
		Pds::Matrix &	B3
	)

static

Convierte elemento a elemento 3 matrices a 3 matrices.

Parámetros

[in]	func	Función que procesa os elementos de las matrices A1, A2 y A3.
[in]	A1	Primera matriz a procesar.
[in]	A2	Segunda matriz a procesar.
[in]	A3	Tercera matriz a procesar.
[out]	B1	Primera matriz resultado.
[out]	B2	Segunda matriz resultado.
[out]	B3	Tercera matriz resultado.

Devuelve: Retorna true si todas las matrices tienen el mismo tamaño no vacio o false si no. En caso de error no modifica las matrices de salida.

◆ IsSampleBlock()

static bool Pds::Matrix::IsSampleBlock ( const std::vector< Pds::Matrix > & Block )

static

Verifica que el bloque (std::vector<Pds::Matrix>) sea un vector no vacío de matrices no nulas y similares. Es decir un Hiperrectángulo.

Parámetros

[in] Block Un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix).

Devuelve: Retorna true si el vector no está vacío y todas las matrices son iguales y no vacías.

Ejemplos: example_matrix_static_matrix.cpp.

◆ FlattenSampleBlock()

static Pds::Vector Pds::Matrix::FlattenSampleBlock ( const std::vector< Pds::Matrix > & Block )

static

Convierte a Pds::vector un SampleBlock.

La converción es realizada vectorizando cada matriz concatenando sus columnas, esta concatenación se repite desde la primera matriz Block[0] hasta la última Block[N-1].

Parámetros

[in] Block Un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix).

Devuelve: Retorna un Pds::Vector que representa la linearización de un SampleBlock. Se retorna un vector vacio si alguna de las matrices en el SampleBlock está vacia.

Ejemplos: example_matrix_static_matrix.cpp.

◆ RandNSampleBlock()

static std::vector< Pds::Matrix > Pds::Matrix::RandNSampleBlock	(	unsigned int	N,
		const Pds::Size &	Sz
	)

static

Crea un bloque (std::vector<Pds::Matrix>) con matrices no nulas y similares inicializadas con Pds::RandN().

Parámetros

[in]	N	Número de capas del sample block.
[in]	Sz	Tamaño de cada matriz en el sample block.

Devuelve: Retorna un sample block Out o un vector vacio (Out.size()==0) en caso de error .

Ejemplos: example_matrix_static_matrix.cpp y example_ra_color2.cpp.

◆ ZerosSampleBlock()

static std::vector< Pds::Matrix > Pds::Matrix::ZerosSampleBlock	(	unsigned int	N,
		const Pds::Size &	Sz
	)

static

Crea un bloque (std::vector<Pds::Matrix>) con matrices no nulas y similares inicializadas con Pds::Zeros().

Parámetros

[in]	N	Número de capas del sample block.
[in]	Sz	Tamaño de cada matriz en el sample block.

Devuelve: Retorna un sample block Out o un vector vacio (Out.size()==0) en caso de error .

Ejemplos: example_matrix_static_matrix.cpp.

◆ MaxPoolingSampleBlock()

static std::vector< Pds::Matrix > Pds::Matrix::MaxPoolingSampleBlock	(	const std::vector< Pds::Matrix > &	A,
		unsigned int	LinPool,
		unsigned int	ColPool
	)

static

Aplica max pooling a cada matriz $\mathbf{A}[n]$
de $L_\mathbf{An}$ lineas y $C_\mathbf{An}$ columnas.

La matriz resultante $\mathbf{B}[n]$ tendrá $L_\mathbf{Bn}=ceil(L_\mathbf{An}/LinPool)$ lineas y $C_\mathbf{Bn}=ceil(C_\mathbf{An}/ColPool)$ columnas.

Parámetros

[in]	A	SampleBlock a aplicar maxpooling.
[in]	LinPool	Pooling entre lineas.
[in]	ColPool	Pooling entre columnas.

Devuelve: Retorna la matriz B resultado de aplicar maxpooling.

Ejemplos: example_matrix_dsp.cpp.

◆ MeanSampleBlock()

static Pds::Matrix Pds::Matrix::MeanSampleBlock ( const std::vector< Pds::Matrix > & Block )

static

Calcula A,la matriz media de un conjunto de N matrizes agrupadas en un std::vector.

$A=\frac{Block[0]+Block[1]+...+Block[N-1]}{N}$

Parámetros

[in] Block Vector std::vector con N elementos Pds::Matrix.

Devuelve: Retorna la matriz media de un conjunto de N matrizes agrupadas en un std::vector.

◆ GetSamples() [1/2]

static Pds::Matrix Pds::Matrix::GetSamples ( const std::vector< Pds::Matrix > & Block )

static

Convierte las muestras de un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos, en una matriz Pds::Matrix(L,N). Lee los datos de la columna actual y pasa a la siguiente, desde la columna 0.

Parámetros

[in] Block Un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos.

Devuelve: Retorna una matriz de L lineas y N columnas. en caso de error se retorna una matriz vacía.

Ejemplos: example_matrix_static_matrix.cpp.

◆ GetSampleRaw() [1/2]

static bool Pds::Matrix::GetSampleRaw	(	const std::vector< Pds::Matrix > &	Block,
		unsigned int	lin,
		unsigned int	col,
		Pds::Vector &	x
	)

static

Extrae una muestra de un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos, a un vector Pds::Vector(N).

Atención: No verifica si el elemento existe en cada matriz del SampleBlock. No verifica si todas las matrices son del mismo tamaño.

Parámetros

[in]	Block	Un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos.
[in]	lin	Linea a extraer.
[in]	col	Columna a extraer.
[in]	x	Este vector debe ser no vacio de N elementos, caso contrario retorna false y no se cargan valores.

Devuelve: Retorna true si todo fue bien o false si no.

Ejemplos: example_matrix_sampleblock.cpp.

◆ GetSampleRaw() [2/2]

static bool Pds::Matrix::GetSampleRaw	(	const std::vector< Pds::Matrix > &	Block,
		unsigned int	id,
		Pds::Vector &	x
	)

static

Extrae una muestra de un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos, a un vector Pds::Vector(N).

Atención: No verifica si el elemento existe en cada matriz del SampleBlock. No verifica si todas las matrices son del mismo tamaño.

Parámetros

[in]	Block	Un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos.
[in]	id	ID a extraer.
[in]	x	Este vector debe ser no vacio de N elementos, caso contrario retorna false y no se cargan valores.

Devuelve: Retorna true si todo fue bien o false si no.

◆ GetSamples() [2/2]

static Pds::Matrix Pds::Matrix::GetSamples	(	const std::vector< Pds::Matrix > &	Block,
		const std::vector< unsigned int >	Id
	)

static

Convierte M muestras de un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos, en una matriz Pds::Matrix(M,N).

Parámetros

[in]	Block	Un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) de L elementos.
[in]	Id	Vector con M indices que representan las muestras a ser seleccionadas.

Devuelve: Retorna una matriz de M lineas y N columnas. en caso de error se retorna una matriz vacía.

◆ ImportBmpFile()

static std::vector< Pds::Matrix > Pds::Matrix::ImportBmpFile ( const std::string & bmpfilename )

static

Lee matrices de un archivo binario en formato BMP.

Atención

Solo lee matrices con :

Suported bmp files
Without compression
Number of planes equal to 1
8,16,24 o 32 bits by pixel.

Parámetros

[in] bmpfilename Nombre del archivo donde se leeran los datos.

Devuelve: Retorna un vector de matrices, una matriz por cada byte en un pixel.

Ejemplos: example_ra_color2.cpp.

◆ ImportBmpFileAsGray()

static Pds::Matrix Pds::Matrix::ImportBmpFileAsGray ( const std::string & bmpfilename )

static

Retorna una matriz en escala de grises, de 0 a 255.

Pds::Matrix IMG;

IMG=Pds::Matrix::ImportBmpFileAsGray("/some/path/with/image.bmp");

Pds::Matrix::ImportBmpFileAsGray

static Pds::Matrix ImportBmpFileAsGray(const std::string &bmpfilename)

Retorna una matriz en escala de grises, de 0 a 255.

Parámetros

[in] bmpfilename Directorio de donde se leerá la imagen BMP.

Devuelve: Retorna una matriz en escala de grises, de 0 a 255.

◆ ExportBmpFile() [2/2]

static bool Pds::Matrix::ExportBmpFile	(	const Pds::Matrix &	R,
		const Pds::Matrix &	G,
		const Pds::Matrix &	B,
		const std::string &	bmpfilename
	)

static

Escribe en una matriz en un archivo binario en formato BMP. Losdatos deben ir de 0 a 255, valores superiores o inferiores serán truncados.

Parámetros

[in]	R	Matriz con colores red 0<=r<=255.
[in]	G	Matriz con colores green 0<=r<=255.
[in]	B	Matriz con colores blue 0<=r<=255.
[in]	bmpfilename	Nombre del archivo donde se escribirán los datos.

Devuelve: Retorna true si todo fue bien o false si no.

◆ ExportAsGif()

static bool Pds::Matrix::ExportAsGif	(	const std::vector< Pds::Matrix > &	Block,
		const std::string &	filename,
		unsigned int	delay = `100`,
		const unsigned char	colormap[256][3] = `Pds::Colormap::Gray`
	)

static

Salva el bloque (std::vector<Pds::Matrix>) en una imagen GIF.

Parámetros

[in]	Block	Un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix) del mismo tamaño.
[in]	filename	Archivo donde se salvará la imagen en formato GIF.
[in]	delay	Retraso entre frames (en centesimas de segundos) en el archivo GIF.
[in]	colormap	Mapa de colores. Ejemplo: Pds::Colormap::Jet, Pds::Colormap::Bone,

Devuelve: Retorna true si todo fue bien y o false si no.

◆ ExportSampleBlockXmlToString()

static std::string Pds::Matrix::ExportSampleBlockXmlToString ( const std::vector< Pds::Matrix > & Block )

static

Retorna un std::string en formato Xml con el contenido del SampleBlock.

Por exemplo si guardamos un SampleBlock A={Pds::Eye(3),Pds::Ones(3)} en el std::string se escribirá:

<SampleBlock>
<Nel>2</Nel>
<Matrix>
<Nlin>3</Nlin>
<Ncol>3</Ncol>
<Array>
1       0       0
0       1       0
0       0       1
</Array>
</Matrix>
<Matrix>
<Nlin>3</Nlin>
<Ncol>3</Ncol>
<Array>
1       1       1
1       1       1
1       1       1
</Array>
</Matrix>
</SampleBlock>

Parámetros

[in] Block Un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix).

Devuelve: Retorna un std::string en formato Xml con el contenido de la matriz.

Ejemplos: example_matrix_export_sample_block.cpp.

◆ ImportSampleBlockXmlFromString()

static std::vector< Pds::Matrix > Pds::Matrix::ImportSampleBlockXmlFromString ( const std::string & str )

static

Carga el contenido de una std::vector<Pds::Matrix> desde un std::string en formato Xml.

Si la lectura es satisfactoria se retorna un nuevo std::vector<Pds::Matrix>, en caso de error el vector estará vacio, es decir size()==0.

Por exemplo si tenemos un std::string str con el texto:

<SampleBlock>
<Nel>2</Nel>
<Matrix>
<Nlin>3</Nlin>
<Ncol>3</Ncol>
<Array>
1       0       0
0       1       0
0       0       1
</Array>
</Matrix>
<Matrix>
<Nlin>3</Nlin>
<Ncol>3</Ncol>
<Array>
1       1       1
1       1       1
1       1       1
</Array>
</Matrix>
</SampleBlock>

Podremos leer el contenido y cargarlo en A usando:

A=Pds::Matrix::ImportSampleBlockXmlFromString(str);

Este formato de almacenamiento de datos proviene de usar Pds::Matrix::ExportSampleBlockXmlToString().

Parámetros

[in] str El std::string donde se leerán los datos.

Devuelve: Retorna una SampleBlock de tipo std::vector<Pds::Matrix>.

Ejemplos: example_matrix_export_sample_block.cpp.

◆ ExportSampleBlockXmlToStream()

static bool Pds::Matrix::ExportSampleBlockXmlToStream	(	std::ofstream &	myfile,
		const std::vector< Pds::Matrix > &	Block
	)

static

Retorna un std::string en formato Xml con el contenido del SampleBlock.

Por exemplo si guardamos un SampleBlock A={Pds::Eye(3),Pds::Ones(3)} en el std::string se escribirá:

<SampleBlock>
<Nel>2</Nel>
<Matrix>
<Nlin>3</Nlin>
<Ncol>3</Ncol>
<Array>
1       0       0
0       1       0
0       0       1
</Array>
</Matrix>
<Matrix>
<Nlin>3</Nlin>
<Ncol>3</Ncol>
<Array>
1       1       1
1       1       1
1       1       1
</Array>
</Matrix>
</SampleBlock>

Parámetros

[in]	myfile	Stream de salida.
[in]	Block	Un bloque (std::vector<Pds::Matrix>) de N matrices (Pds::Matrix).

Devuelve: Retorna un true si todo fue bien o false si no.

◆ IsBatchBlock()

static bool Pds::Matrix::IsBatchBlock ( const std::vector< std::vector< Pds::Matrix > > & Tensor )

static

Verifica que el tensor (std::vector<std::vector<Pds::Matrix>>) sea un vector de vectores no vacíos de matrices no nulas y similares. Es decir un Hiperrectángulo.

Parámetros

[in] Tensor Un bloque (std::vector<std::vector<Pds::Matrix>>) de L sample block con N matrices (Pds::Matrix).

Devuelve: Retorna true si el vector no está vacío y todas las matrices son iguales y no vacías.

Ejemplos: example_matrix_static_matrix.cpp.

◆ RandNBatchBlock()

static std::vector< std::vector< Pds::Matrix > > Pds::Matrix::RandNBatchBlock	(	unsigned int	L,
		unsigned int	N,
		const Pds::Size &	Sz
	)

static

Crea un tensor (std::vector<std::vector<Pds::Matrix>>) con matrices no nulas y similares inicializadas con Pds::RandN().

Parámetros

[in]	L	Número de sample block.
[in]	N	Número de capas en cada sample block.
[in]	Sz	Tamaño de cada una de las matrices en todos los sample block.

Devuelve: Retorna un sample block Out o un vector vacio (Out.size()==0) en caso de error .

Ejemplos: example_matrix_export_tensor_block.cpp y example_matrix_static_matrix.cpp.

◆ ZerosBatchBlock()

static std::vector< std::vector< Pds::Matrix > > Pds::Matrix::ZerosBatchBlock	(	unsigned int	L,
		unsigned int	N,
		const Pds::Size &	Sz
	)

static

Crea un tensor (std::vector<std::vector<Pds::Matrix>>) con matrices no nulas y similares inicializadas con Pds::Zeros().

Parámetros

[in]	L	Número de sample block.
[in]	N	Número de capas en cada sample block.
[in]	Sz	Tamaño de cada una de las matrices en todos los sample block.

Devuelve: Retorna un sample block Out o un vector vacio (Out.size()==0) en caso de error .

Ejemplos: example_matrix_static_matrix.cpp.

◆ ExportBatchBlockXmlToString()

static std::string Pds::Matrix::ExportBatchBlockXmlToString ( const std::vector< std::vector< Pds::Matrix > > & Block )

static

Retorna un std::string en formato Xml con el contenido del BatchBlock.

Por exemplo si guardamos un BatchBlock A={{Pds::Eye(3),Pds::Ones(3)},{Pds::Eye(3),Pds::Ones(3)}} en el std::string se escribirá:

<BatchBlock>
<Nel>2</Nel>
<SampleBlock>
...
</SampleBlock>
<SampleBlock>
...
</SampleBlock>
</BatchBlock>

Parámetros

[in] Block Un bloque (std::vector<std::vector<Pds::Matrix>>) de N*M matrices (Pds::Matrix).

Devuelve: Retorna un std::string en formato Xml con el contenido del BatchBlock.

Ejemplos: example_matrix_export_tensor_block.cpp.

◆ ImportBatchBlockXmlFromString()

static std::vector< std::vector< Pds::Matrix > > Pds::Matrix::ImportBatchBlockXmlFromString ( const std::string & str )

static

Carga el contenido de una std::vector<std::vector<Pds::Matrix>> desde un std::string en formato Xml.

Si la lectura es satisfactoria se retorna un nuevo std::vector<std::vector<Pds::Matrix>>, en caso de error el vector estará vacio, es decir size()==0.

Por exemplo si tenemos un std::string str con el texto:

<BatchBlock>
<Nel>2</Nel>
<SampleBlock>
...
</SampleBlock>
<SampleBlock>
...
</SampleBlock>
</BatchBlock>

Podremos leer el contenido y cargarlo en A usando:

A=Pds::Matrix::ImportBatchBlockXmlFromString(str);

Este formato de almacenamiento de datos proviene de usar Pds::Matrix::ExportBatchBlockXmlToString().

Parámetros

[in] str El std::string donde se leerán los datos.

Devuelve: Retorna una BatchBlock de tipo std::vector<std::vector<Pds::Matrix>>.

Ejemplos: example_matrix_export_tensor_block.cpp.

◆ ExportBatchBlockXmlToStream()

static bool Pds::Matrix::ExportBatchBlockXmlToStream	(	std::ofstream &	myfile,
		const std::vector< std::vector< Pds::Matrix > > &	Block
	)

static

Escribe en un std::ofstream en formato Xml con el contenido del BatchBlock.

Por exemplo si guardamos un BatchBlock A={{Pds::Eye(3),Pds::Ones(3)},{Pds::Eye(3),Pds::Ones(3)}} en el std::ofstream se escribirá:

<BatchBlock>
<Nel>2</Nel>
<SampleBlock>
...
</SampleBlock>
<SampleBlock>
...
</SampleBlock>
</BatchBlock>

Parámetros

[in]	myfile	Stream de salida.
[in]	Block	Un bloque (`std::vector<std::vector<Pds::Matrix>>`) de N*M matrices (Pds::Matrix).

Devuelve: Retorna un true si todo fue bien o false si no.

Ejemplos: example_matrix_export_tensor_block.cpp.

◆ FromString()

static Pds::Matrix Pds::Matrix::FromString ( const std::string & str )

static

Convierte un sdt::string a una Matriz de Nlin lineas y Ncol columnas.

Parámetros

[in] str Cadena a leer.

Devuelve: Retorna una matriz. en caso de error se retorna una matriz vacía.

Ejemplos: example_matrix_static_matrix.cpp.

◆ T()

Pds::Matrix Pds::Matrix::T ( void ) const

Transpuesta de si mismo (A), el resultado es cargado en B.

$B \leftarrow transpose(A)$

Pds::Matrix A(4,4);
Pds::Matrix B;
 
A.FillRandU();
 
B=A.T();
 
std::cout<<B;

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_binarytreenode.cpp, example_circle_create.cpp, example_ellipse_create.cpp, example_ellipse_getellipse.cpp, example_funcvector_space.cpp, example_matrix_algebra.cpp, example_matrix_algebra_cholesky.cpp, example_matrix_algebra_eig.cpp, example_matrix_algebra_eig2.cpp, example_matrix_dsp_hist.cpp, example_matrix_knearest.cpp, example_matrix_operators_binary.cpp, example_matrix_sampleblock.cpp, example_matrix_static_matrix.cpp, example_matrixfunc.cpp, example_matrixmath.cpp, example_matrixmath_dsp.cpp, example_matrixmath_erf.cpp, example_optadam_create.cpp, example_ra_indices.cpp, example_regression_fitting.cpp, example_vector_create.cpp, example_vector_dsp.cpp, example_vector_dsp_conv.cpp, example_vector_dsp_conv1d.cpp, example_vector_json.cpp, example_vector_nearestk.cpp, example_vector_operator_unit.cpp, example_vector_poly.cpp, example_vector_sorting.cpp y example_vectorfunc.cpp.

◆ MtM() [1/2]

Pds::Matrix Pds::Matrix::MtM ( void ) const

Retorna A.T()*A cargado en B.

$B \leftarrow A^{T}A$

Pds::Matrix A(4,4);
Pds::Matrix B;
 
A.FillRandU();
 
B=A.MtM();
 
std::cout<<B;

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operator_unario.cpp.

◆ MtM() [2/2]

Pds::Matrix Pds::Matrix::MtM ( const Pds::Matrix & B ) const

Retorna A.T()*A cargado en B.

$C \leftarrow (A-B)^{T}(A-B)$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.FillRandU();
B.FillRandU();
 
C=A.MtM(B);
 
std::cout<<C;

Parámetros

[in] B Matriz de resta.

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ MMt() [1/2]

Pds::Matrix Pds::Matrix::MMt ( void ) const

Retorna A*A.T() cargado en B.

$B \leftarrow A*A^{T}$

Pds::Matrix A(4,4);
Pds::Matrix B;
 
A.FillRandU();
 
B=A.MMt();
 
std::cout<<B;

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operator_unario.cpp.

◆ MMt() [2/2]

Pds::Matrix Pds::Matrix::MMt ( const Pds::Matrix & B ) const

Retorna A*A.T() cargado en B.

$C \leftarrow (A-B)*(A-B)^{T}$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.FillRandU();
B.FillRandU();
 
C=A.MMt(B);
 
std::cout<<C;

Parámetros

[in] B Matriz de resta.

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ Inv()

Pds::Matrix Pds::Matrix::Inv ( double * rcond = NULL ) const

Retorna la matriz inversa.

rcond es:

$rcond \leftarrow \frac{1.0}{||A||_1 ||A^{-1}||_1}$

Atención: Internamente es usado el método de eliminación Gaussiana para obtener la inversa.

Parámetros

[out] rcond Esta variable es cargada con el valor del reciproco del condicional de la matriz. Si esta es la matriz A. Si la matriz esta bien condicionada entonces rcond es próximo a 1.0 y si la matriz esta pobremente condicionada este valor estará proximo a 0.0. Si la variable rcond no es entregada entonces sera mostrado un mensaje de advertencia por consola si el valor de rcond es menor a Pds::Ra::WarningRCond.

Devuelve: Retorna la matriz inversa si todo fue bien o una matriz vacia (.IsEmpty()==true) si no es posible calcular la inversa.

Ejemplos: example_matrixfunc.cpp.

◆ PInv()

Pds::Matrix Pds::Matrix::PInv ( double * rcond = NULL ) const

Procesa esta matriz A y retorna B la matriz pseudo inversa de Moore Penrose.

$B \leftarrow (A^T A)^{-1}A^T$

$rcond \leftarrow \frac{1.0}{||A^T A||_1 ||(A^T A)^{-1}||_1}$

Atención: Internamente es usado el método de eliminación Gaussiana para en el cáculo de la inversa.

Parámetros

[out] rcond Esta variable es cargada con el valor del reciproco del condicional de la matriz . Si la matriz está bien condicionada entonces rcond es próximo a 1.0 y si la matriz esta pobremente condicionada este valor estará proximo a 0.0. Si la variable rcond no es entregada entonces sera mostrado un mensaje de advertencia por consola si el valor de rcond es menor a Pds::Ra::WarningRCond.

Devuelve: Retorna la matriz inversa si todo fue bien o una matriz vacia (.IsEmpty()==true) si no es posible calcular la inversa.

◆ operator-() [1/4]

Pds::Matrix Pds::Matrix::operator- ( void ) const

Cambia de signo a si mismo (A), el resultado es cargado en B. Este operador es similar al método unario Minus.

$B \leftarrow -A$

Pds::Matrix A(4,4);
Pds::Matrix B;
 
A.Fill(2.0);
 
B=-A;
 
std::cout<<B;

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vazia (this->IsEmpty() igual a true) en caso de error.

◆ Minus()

Pds::Matrix Pds::Matrix::Minus ( void ) const

Cambia de signo a si mismo (A), el resultado es cargado en B. Este método es similar al operador unario -.

$B \leftarrow -A$

Pds::Matrix A(4,4);
Pds::Matrix B;
 
A.Fill(2.0);
 
B=A.Minus();
 
std::cout<<B;

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ operator+() [1/4]

Pds::Matrix Pds::Matrix::operator+ ( void ) const

Asigna el signo + a si mismo (A), el resultado es cargado en B. Este operador es similar al método unario Plus.

$B \leftarrow +A$

Pds::Matrix A(4,4);
Pds::Matrix B;
 
A.Fill(2.0);
 
B=+A;
 
std::cout<<B;

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ Plus()

Pds::Matrix Pds::Matrix::Plus ( void ) const

Asigna el signo + a si mismo (A), el resultado es cargado en B. Este método es similar al operador unario +.

$B \leftarrow +A$

Pds::Matrix A(4,4);
Pds::Matrix B;
 
A.Fill(2.0);
 
B=A.Plus();
 
std::cout<<B;

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vazia (this->IsEmpty() igual a true) en caso de error.

◆ operator*() [1/3]

Pds::Matrix Pds::Matrix::operator* ( double b ) const

Multiplica con sigo mismo (A), un valor b y el resultado es cargado en C. Este operador es similar al método Mul()

$C \leftarrow A*b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=A*2.0;
 
std::cout<<C;

Parámetros

[in] b el valor a multiplicar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: Mul

◆ operator*() [2/3]

Pds::Matrix Pds::Matrix::operator* ( const Pds::Matrix & B ) const

Multiplica con sigo mismo (A), una matriz B y el resultado es cargado en C. Este operador es similar al método Mul()

$C \leftarrow A*B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A*B;
 
std::cout<<C;

Parámetros

[in] B la matriz a multiplicar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: Mul

◆ Mul() [1/4]

Pds::Matrix Pds::Matrix::Mul ( double b ) const

Multiplica con sigo mismo (A), un valor b y el resultado es cargado en C. Este método es similar al operador *.

$C \leftarrow A*b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=A.Mul(2.0);
 
std::cout<<C;

Parámetros

[in] b el valor a multiplicar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operators_binary.cpp.

◆ Mul() [2/4]

Pds::Matrix Pds::Matrix::Mul ( const Pds::Matrix & B ) const

Multiplica con sigo mismo (A), una matriz B y el resultado es cargado en C. Este método es similar al operador *.

$C \leftarrow A*B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.Mul(B);
 
std::cout<<C;

Parámetros

[in] B la matriz a multiplicar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ Mul() [3/4]

bool Pds::Matrix::Mul	(	const Pds::Matrix &	B,
		Pds::Matrix &	Out
	)		const

Multiplica con sigo mismo (A), una matriz B y el resultado es cargado en Out. Este método es similar al operador *.

$Out \leftarrow A*B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix Out(4,4);
 
A.Fill(2.0);
B.Fill(1.0);
 
A.Mul(B,Out);
 
std::cout<<Out;

Parámetros

[in]	B	La matriz a multiplicar
[in]	Out	El resultado de la multiplicación. El tamaño de la matriz deve ser el correcto o retorna false y no carga el resultado.

Devuelve: Retorna true si todo fue bien o false en caso contrario.

◆ Mul() [4/4]

Pds::Matrix Pds::Matrix::Mul ( const Pds::Vector & B ) const

Multiplica con sigo mismo (A), un vector B y el resultado es cargado en C. Este método es similar al operador *.

$C \leftarrow A*B$

Pds::Matrix A(4,4);
Pds::Vector B(4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.Mul(B);
 
std::cout<<C;

Parámetros

[in] B El vector a multiplicar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ MulRowMatrix()

Pds::Matrix Pds::Matrix::MulRowMatrix ( const Pds::Matrix & B ) const

[Elemento a elemento] Multiplica con sigo mismo (A), una matriz B linea y el resultado es cargado en C. La unica linea de B es Multiplicada a cada linea de A.

$C \leftarrow A/B$

Pds::Matrix A(4,4);
Pds::Matrix B(1,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.MulRowMatrix(B);
 
std::cout<<C;

Parámetros

[in] B la matriz que suma

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error. Existe error si B esta vacio o si B no es una matri linea.

◆ MulComp() [1/3]

Pds::Matrix Pds::Matrix::MulComp	(	double	b,
		const Pds::Vector &	B
	)		const

Multiplica con sigo mismo (A), un vector [b;B] y el resultado es cargado en C.

$C \leftarrow A*[b;B]$

Pds::Matrix A(4,4);
Pds::Vector B(3);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.MulComp(3,B);
 
std::cout<<C;

Parámetros

[in]	b	El pedazo de arriba del vector a multiplicar
[in]	B	El pedazo de abajo del vector a multiplicar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operators_binary2.cpp.

◆ CompMul()

Pds::Matrix Pds::Matrix::CompMul	(	double	b,
		const Pds::Matrix &	B
	)		const

Multiplica con sigo mismo (A), previa composición, una matriz B y el resultado es cargado en C. El valor b es colocado en toda una columna.

$C \leftarrow [b~A]*B$

Pds::Matrix A(4,4);
Pds::Vector B(5);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.CompMul(1,B);
 
std::cout<<C;

Parámetros

[in]	b	El valor a usar en la columna de la composición.
[in]	B	La matriz a multiplicar.

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operators_binary2.cpp.

◆ MulComp() [2/3]

bool Pds::Matrix::MulComp	(	double	b,
		const Pds::Vector &	B,
		Pds::Vector &	Out
	)		const

Multiplica con sigo mismo (A), un vector [b;B] y el resultado es cargado en Out. Este método es similar al operador *.

$Out \leftarrow A*\begin{bmatrix}b\\B\end{bmatrix}$

Pds::Matrix A(4,4);
Pds::Vector B(3);
Pds::Vector Out(4);
 
A.Fill(2.0);
B.Fill(1.0);
 
A.MulComp(-1,B,Out);
 
std::cout<<Out;

Parámetros

[in]	b	El pedazo de arriba del vector a multiplicar
[in]	B	El pedazo de abajo del vector a multiplicar
[out]	Out	El vector resultante de la multiplicación.

Devuelve: Retorna tru si todo fue bien y false si no. El método verifica los tamaños de B y Out, si son incorrectos se retorna false y no se hace nada.

◆ MulComp() [3/3]

bool Pds::Matrix::MulComp	(	double	b,
		const Pds::Matrix &	B,
		Pds::Matrix &	Out
	)		const

Multiplica con sigo mismo (A), un vector [b;B] y el resultado es cargado en Out. Este método es similar al operador *.

$Out \leftarrow A*\begin{bmatrix}b\\B\end{bmatrix}$

Pds::Matrix A(4,4);
Pds::Matrix B(3,1);
Pds::Matrix Out(4,1);
 
A.Fill(2.0);
B.Fill(1.0);
 
A.MulComp(-1,B,Out);
 
std::cout<<Out;

Parámetros

[in]	b	El pedazo de arriba de la matriz a multiplicar
[in]	B	El pedazo de abajo de la matriz a multiplicar
[out]	Out	El vector resultante de la multiplicación.

Devuelve: Retorna tru si todo fue bien y false si no. El método verifica los tamaños de B y Out, si son incorrectos se retorna false y no se hace nada.

◆ MulT()

Pds::Matrix Pds::Matrix::MulT ( const Pds::Matrix & B ) const

Multiplica con sigo mismo (A), la transpuesta de una matriz B y el resultado es cargado en C. Este método es similar al operador *.

$C \leftarrow A*B^T$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.MulT(B);
 
std::cout<<C;

Parámetros

[in] B la matriz a multiplicar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ TMul()

Pds::Matrix Pds::Matrix::TMul ( const Pds::Matrix & B ) const

Multiplica con la transpuesta de sí mismo (A^T), la matriz B y el resultado es cargado en C. Este método es similar al operador *.

$C \leftarrow A^T*B$

Pds::Matrix A(4,2);
Pds::Matrix B(4,2);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.TMul(B);
 
std::cout<<C;

Parámetros

[in] B la matriz a multiplicar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operators_binary.cpp y example_optadam_create.cpp.

◆ operator+() [2/4]

Pds::Matrix Pds::Matrix::operator+ ( double b ) const

[Elemento a elemento] Suma con sigo mismo (A), un valor b y el resultado es cargado en C. Este operador es similar al método Add()

$C \leftarrow A+b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=A+2.0;
 
std::cout<<C;

Parámetros

[in] b El valor a sumar

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vazia (this->IsEmpty() igual a true) en caso de error.

Ver también: Add

◆ operator+() [3/4]

Pds::Matrix Pds::Matrix::operator+ ( const Pds::Matrix & B ) const

[Elemento a elemento] Suma con sigo mismo (A), una matriz B y el resultado es cargado en C. Este operador es similar al método Add()

$C \leftarrow A+B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A+B;
 
std::cout<<C;

Parámetros

[in] B la matriz a sumar

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vazia (this->IsEmpty() igual a true) en caso de error.

Ver también: Add

◆ Add() [1/2]

Pds::Matrix Pds::Matrix::Add ( double b ) const

[Elemento a elemento] Suma con sigo mismo (A), una valor b y el resultado es cargado en C. Este método es similar al operador +

$C \leftarrow A+b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=A.Add(2.0);
 
std::cout<<C;

Parámetros

[in] b El valor a sumar

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vazia (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operators_binary.cpp.

◆ Add() [2/2]

Pds::Matrix Pds::Matrix::Add ( const Pds::Matrix & B ) const

[Elemento a elemento] Suma con sigo mismo (A), una matriz B y el resultado es cargado en C. Este metodo es similar al operador +

$C \leftarrow A+B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.Add(B);
 
std::cout<<C;

Parámetros

[in] B la matriz a sumar

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vazia (this->IsEmpty() igual a true) en caso de error.

◆ operator-() [2/4]

Pds::Matrix Pds::Matrix::operator- ( double b ) const

[Elemento a elemento] Resta con sigo mismo (A), un valor b y el resultado es cargado en C. Este operador es similar al método Sub()

$C \leftarrow A-b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=A-2.0;
 
std::cout<<C;

Parámetros

[in] b El valor a restar

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: Add

◆ operator-() [3/4]

Pds::Matrix Pds::Matrix::operator- ( const Pds::Matrix & B ) const

[Elemento a elemento] Resta con sigo mismo (A), una matriz B y el resultado es cargado en C. Este operador es similar al método Sub

$C \leftarrow A-B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A-B;
 
std::cout<<C;

Parámetros

[in] B la matriz que resta

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ Sub() [1/2]

Pds::Matrix Pds::Matrix::Sub ( double b ) const

[Elemento a elemento] Resta con sigo mismo (A), una valor b y el resultado es cargado en C. Este método es similar al operador -

$C \leftarrow A-b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=A.Sub(2.0);
 
std::cout<<C;

Parámetros

[in] b El valor a restar

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ Sub() [2/2]

Pds::Matrix Pds::Matrix::Sub ( const Pds::Matrix & B ) const

[Elemento a elemento] Resta con sigo mismo (A), una matriz B y el resultado es cargado en C. Este método es similar al operador -

$C \leftarrow A-B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.Sub(B);
 
std::cout<<C;

Parámetros

[in] B la matriz que resta

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ AddRowMatrix()

Pds::Matrix Pds::Matrix::AddRowMatrix ( const Pds::Matrix & B ) const

Suma con sigo mismo (A), una matriz B linea y el resultado es cargado en C. La unica linea de B es sumada a cada linea de A.

$C \leftarrow A+B$

Pds::Matrix A(4,4);
Pds::Matrix B(1,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.AddRowMatrix(B);
 
std::cout<<C;

Parámetros

[in] B la matriz que suma

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error. Existe error si B esta vacio o si B no es una matri linea.

Ejemplos: example_matrix_operators_binary.cpp y example_octave_pairwisescatterxy.cpp.

◆ SubRowMatrix()

Pds::Matrix Pds::Matrix::SubRowMatrix ( const Pds::Matrix & B ) const

Resta con sigo mismo (A), una matriz B linea y el resultado es cargado en C. La unica linea de B es restada a cada linea de A.

$C \leftarrow A-B$

Pds::Matrix A(4,4);
Pds::Matrix B(1,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.SubRowMatrix(B);
 
std::cout<<C;

Parámetros

[in] B la matriz que resta

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error. Existe error si B esta vacio o si B no es una matri linea.

Ejemplos: example_matrix_operators_binary.cpp.

◆ operator/() [1/3]

Pds::Matrix Pds::Matrix::operator/ ( double b ) const

[Elemento a elemento] Divide con sigo mismo (A), un valor b y el resultado es cargado en C. Este operador es similar al método Div()

$C \leftarrow A/b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=A/2.0;
 
std::cout<<C;

Parámetros

[in] b el valor a dividir

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: Mul

◆ operator/() [2/3]

Pds::Matrix Pds::Matrix::operator/ ( const Pds::Matrix & B ) const

[Elemento a elemento] Divide con sigo mismo (A), elemento a elemento, una matriz B y el resultado es cargado en C. Este método es similar al método .Div()

$C \leftarrow A / B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(1.0);
B.Fill(2.0);
 
C=A/B;
 
std::cout<<C;

Parámetros

[in] B la matriz a dividir

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ Div() [1/2]

Pds::Matrix Pds::Matrix::Div ( double b ) const

[Elemento a elemento] Divide con sigo mismo (A), un valor b y el resultado es cargado en C. Este método es similar al operador /

$C \leftarrow A/b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=A.Div(2.0);
 
std::cout<<C;

Parámetros

[in] b el valor a dividir

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operators_binary.cpp.

◆ Div() [2/2]

Pds::Matrix Pds::Matrix::Div ( const Pds::Matrix & B ) const

[Elemento a elemento] Divide con sigo mismo (A), elemento a elemento, una matriz B y el resultado es cargado en C. Este método es similar al operador /

$C \leftarrow A / B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(1.0);
B.Fill(2.0);
 
C=A.Div(B);
 
std::cout<<C;

Parámetros

[in] B la matriz a dividir

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ DivRowMatrix()

Pds::Matrix Pds::Matrix::DivRowMatrix ( const Pds::Matrix & B ) const

[Elemento a elemento] Divide con sigo mismo (A), una matriz B linea y el resultado es cargado en C. La unica linea de B es dividida a cada linea de A.

$C \leftarrow A/B$

Pds::Matrix A(4,4);
Pds::Matrix B(1,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.DivRowMatrix(B);
 
std::cout<<C;

Parámetros

[in] B la matriz que suma

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error. Existe error si B esta vacio o si B no es una matri linea.

◆ DivBelow()

Pds::Matrix Pds::Matrix::DivBelow ( double b ) const

[Elemento a elemento] Divide con sigo mismo (A), un valor b y el resultado es cargado en C. Este método es similar al operador /

$C \leftarrow b/A$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=A.DivBelow(1.0);
 
std::cout<<C;

Parámetros

[in] b El valor del numerador en la division

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ operator&()

Pds::Matrix Pds::Matrix::operator& ( const Pds::Matrix & B ) const

[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz B y el resultado es cargado en C. Este método es similar al método .Product()

$C \leftarrow A \& B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A&B;
 
std::cout<<C;

Atención

El operador & tiene baja precedencia, por lo que recomendamos usar parentesis (A&B).

Operator Precedence
Precedence	Operator
5	a*b a/b ab
6	a+b a-b
7	<< >>
9	> < >= <=
10	== !=
11	&
12	^

Parámetros

[in] B la matriz a multiplicar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ Product() [1/2]

Pds::Matrix Pds::Matrix::Product ( const Pds::Matrix & B ) const

[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz B y el resultado es cargado en C. Este método es similar al operador &

$C \leftarrow A\&B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.Product(B);
 
std::cout<<C;

Parámetros

[in] B la matriz a multiplicar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operators_binary.cpp.

◆ Product() [2/2]

Pds::Matrix Pds::Matrix::Product	(	double(*)(double)	func,
		const Pds::Matrix &	B
	)		const

[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz func(B) y el resultado es cargado en C. Este método es similar al operador &

$C \leftarrow A\& func(B)$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.Product(func,B);
 
std::cout<<C;

Parámetros

[in]	func	Función a evaluar.
[in]	B	la matriz a multiplicar.

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ Pow() [1/2]

Pds::Matrix Pds::Matrix::Pow ( const Pds::Matrix & B ) const

[Elemento a elemento]Potencia asi mismo (A), elemento a elemento, con una matriz B y el resultado es cargado en C. Este método es similar al operador

$C \leftarrow A^B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
B.Fill(1.0);
 
C=A.Pow(B);
 
std::cout<<C;

Parámetros

[in] B La matriz a exponenciar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operators_binary.cpp.

◆ Pow() [2/2]

Pds::Matrix Pds::Matrix::Pow ( double val ) const

[Elemento a elemento] Potencia asi mismo (A), elemento a elemento, con un valor val y el resultado es cargado en C. Este método es similar al operador

$C \leftarrow A^{val}$

Pds::Matrix A(4,4);
Pds::Matrix val=2;
Pds::Matrix C;
 
A.Fill(2.0);
 
C=A.Pow(val);
 
std::cout<<C;

Parámetros

[in] val Valor a exponenciar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ GreaterThan()

Pds::Matrix Pds::Matrix::GreaterThan ( double b ) const

[Elemento a elemento] Calcula con sigo mismo (A), si (A) es mayor que un valor b y el resultado es cargado en C. Este método es similar al operador >

$C \leftarrow A>b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.FillId();
 
C=A.GreaterThan(4);
 
std::cout<<C;

Parámetros

[in] b el valor a comparar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ Geq() [1/2]

Pds::Matrix Pds::Matrix::Geq ( double b ) const

[Elemento a elemento] Calcula con sigo mismo (A), si (A) es mayor o igual que un valor b y el resultado es cargado en C. Este método es similar al operador >=

$C \leftarrow A>=b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.FillId();
 
C=A.Geq(4);
 
std::cout<<C;

Parámetros

[in] b el valor a comparar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_kernel_gaussian.cpp, example_matrix_operators_binary.cpp y example_optadam_create.cpp.

◆ Geq() [2/2]

Pds::Matrix Pds::Matrix::Geq ( Pds::Matrix B ) const

[Elemento a elemento] Calcula con sigo mismo (A), si (A) es mayor que un valor (B) y el resultado es cargado en C. Este método es similar al operador >=

$C \leftarrow A>=B$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.FillId();
 
C=A.Geq(B);
 
std::cout<<C;

Parámetros

[in] B Matriz a comparar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ Leq() [1/2]

Pds::Matrix Pds::Matrix::Leq ( double b ) const

[Elemento a elemento] Calcula con sigo mismo (A), si (A) es menor que un valor b y el resultado es cargado en C. Este método es similar al operador <=

$C \leftarrow A<=b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.FillId();
 
C=A.Leq(4);
 
std::cout<<C;

Parámetros

[in] b el valor a comparar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operators_binary.cpp.

◆ Leq() [2/2]

Pds::Matrix Pds::Matrix::Leq ( const Pds::Matrix & B ) const

[Elemento a elemento] Calcula con sigo mismo (A), si (A) es menor que un valor B y el resultado es cargado en C. Este método es similar al operador <=

$C \leftarrow A<=B$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.FillId();
 
C=A.Leq(B);
 
std::cout<<C;

Parámetros

[in] B Matriz a comparar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ EqualTo() [1/2]

Pds::Matrix Pds::Matrix::EqualTo ( double b ) const

[Elemento a elemento] Calcula con sigo mismo (A), si (A) es identico a un valor b y el resultado es cargado en C. Este método es similar al operador ==

$C \leftarrow A==b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.FillId();
 
C=A.EqualTo(4);
 
std::cout<<C;

Parámetros

[in] b el valor a comparar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrixmath.cpp.

◆ EqualTo() [2/2]

Pds::Matrix Pds::Matrix::EqualTo ( const Pds::Matrix & B ) const

[Elemento a elemento] Calcula con sigo mismo (A), si (A) es identico a un valor B y el resultado es cargado en C. Este método es similar al operador ==

$C \leftarrow A==B$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.FillId();
 
C=A.EqualTo(B);
 
std::cout<<C;

Parámetros

[in] B Matriz a comparar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ NotEqualTo() [1/2]

Pds::Matrix Pds::Matrix::NotEqualTo ( double b ) const

[Elemento a elemento] Calcula con sigo mismo (A), si (A) no es identico a un valor b y el resultado es cargado en C. Este método es similar al operador !=

$C \leftarrow A!=b$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.FillId();
 
C=A.NotEqualTo(4);
 
std::cout<<C;

Parámetros

[in] b el valor a comparar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ NotEqualTo() [2/2]

Pds::Matrix Pds::Matrix::NotEqualTo ( const Pds::Matrix & B ) const

[Elemento a elemento] Calcula con sigo mismo (A), si (A) no es identico a un valor B y el resultado es cargado en C. Este método es similar al operador !=

$C \leftarrow A!=B$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.FillId();
 
C=A.NotEqualTo(B);
 
std::cout<<C;

Parámetros

[in] B Matriz a comparar

Devuelve: Retorna C con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

◆ EqualToInf()

Pds::Matrix Pds::Matrix::EqualToInf ( void ) const

Verifica si la matriz tiene elementos con valores infinitos.

Los valores infinitos pueden producirse con $+\frac{1}{0},-\frac{1}{0} y \frac{1}{0}$ .

$\left(\begin{matrix} 0 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 1\\ \vdots & \vdots & \vdots & \vdots \\ 1 & 0 & \cdots & 0\\ 0 & 1 & \cdots & 0\\ \end{matrix}\right) \overleftarrow{EqualToInf} \left(\begin{matrix} 1 & NaN & \cdots & NaN\\ 0 & 2 & \cdots & -\infty\\ \vdots & \vdots & \vdots & \vdots \\ \infty & 0 & \cdots & 0\\ 3 & -\infty & \cdots & NaN\\ \end{matrix}\right)$

Devuelve: Retorna una nueva matriz con 1 donde es infinito y 0 donde no lo es.

◆ EqualToNan()

Pds::Matrix Pds::Matrix::EqualToNan ( void ) const

Verifica si la matriz tiene elementos con valores NAN (Not A Number).

Los valores NAN pueden producirse con $\frac{0}{0}$ .

$\left(\begin{matrix} 0 & 1 & \cdots & 1\\ 0 & 0 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 1\\ \end{matrix}\right) \overleftarrow{EqualToNan} \left(\begin{matrix} 1 & NaN & \cdots & NaN\\ 0 & 2 & \cdots & -\infty\\ \vdots & \vdots & \vdots & \vdots \\ \infty & 0 & \cdots & 0\\ 3 & -\infty & \cdots & NaN\\ \end{matrix}\right)$

Devuelve: Retorna una nueva matriz con 1 donde es NAN y 0 donde no lo es.

◆ EqualToFinite()

Pds::Matrix Pds::Matrix::EqualToFinite ( void ) const

Verifica si la matriz tiene elementos con valores finitos (no +inf, no -inf y no NAN).

$\left(\begin{matrix} 1 & 0 & \cdots & 0\\ 1 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots \\ 0 & 1 & \cdots & 1\\ 1 & 0 & \cdots & 0\\ \end{matrix}\right) \overleftarrow{EqualToFinite} \left(\begin{matrix} 1 & NaN & \cdots & NaN\\ 0 & 2 & \cdots & -\infty\\ \vdots & \vdots & \vdots & \vdots \\ \infty & 0 & \cdots & 0\\ 3 & -\infty & \cdots & NaN\\ \end{matrix}\right)$

Devuelve: Retorna una nueva matriz con 1 donde es finito y 0 donde no lo es.

◆ Xor()

Pds::Matrix Pds::Matrix::Xor	(	const Pds::Matrix &	B,
		double	Umbral = `0.5`
	)		const

[Elemento a elemento] Xor con sigo mismo (A), una matriz B y el resultado es cargado en C.

$C \leftarrow A ~ xor ~ B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(1.0);
B.Fill(1.0);
 
C=A.Xor(B);
 
std::cout<<C;

Parámetros

[in]	B	la matriz a Xor
[in]	Umbral	Umbral para binarizar ambas matrices.

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vazia (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operator_binario_bin.cpp.

◆ And()

Pds::Matrix Pds::Matrix::And	(	const Pds::Matrix &	B,
		double	Umbral = `0.5`
	)		const

[Elemento a elemento] And con sigo mismo (A), una matriz B y el resultado es cargado en C.

$C \leftarrow A ~ and ~ B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(1.0);
B.Fill(1.0);
 
C=A.And(B);
 
std::cout<<C;

Parámetros

[in]	B	la matriz a And
[in]	Umbral	Umbral para binarizar ambas matrices.

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vazia (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operator_binario_bin.cpp.

◆ Or()

Pds::Matrix Pds::Matrix::Or	(	const Pds::Matrix &	B,
		double	Umbral = `0.5`
	)		const

[Elemento a elemento] Or con sigo mismo (A), una matriz B y el resultado es cargado en C.

$C \leftarrow A ~ or ~ B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
Pds::Matrix C;
 
A.Fill(1.0);
B.Fill(1.0);
 
C=A.Or(B);
 
std::cout<<C;

Parámetros

[in]	B	la matriz a Or
[in]	Umbral	Umbral para binarizar ambas matrices.

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vazia (this->IsEmpty() igual a true) en caso de error.

Ejemplos: example_matrix_operator_binario_bin.cpp.

◆ operator-=() [1/2]

Pds::Matrix & Pds::Matrix::operator-= ( double b )

Resta y acumula en si mismo (A), un valor b. Este operador es similar al método SubAssig()

$A \leftarrow A-b$

Pds::Matrix A(4,4);
double b=1.2;
B.Fill(1.0);
A-=b;

Parámetros

[in] b El valor a substraer

Devuelve: Retorna el operador de la izquierda (acumulador) con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: SubAssig

◆ operator-=() [2/2]

Pds::Matrix & Pds::Matrix::operator-= ( const Pds::Matrix & B )

Resta y acumula en si mismo (A), una matriz B. Este operador es similar al método SubAssig()

$A \leftarrow A-B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
B.Fill(1.0);
A-=B;

Parámetros

[in] B la matriz a substraer

Devuelve: Retorna el operador de la izquierda (acumulador) con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: SubAssig

◆ SubAssig() [1/3]

bool Pds::Matrix::SubAssig ( double b )

Resta y acumula en si mismo (A), un valor b. Este es similar al operador -=.

$A \leftarrow A-b$

Pds::Matrix A(4,4);
double b=1.2;
A.SubAssig(b);

Parámetros

[in] b valor a substraer

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ SubAssig() [2/3]

bool Pds::Matrix::SubAssig ( const Pds::Matrix & B )

Resta y acumula en si mismo (A), una matriz B. Este es similar al operador -=.

$A \leftarrow A-B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
B.Fill(1.0);
A.SubAssig(B);

Parámetros

[in] B la matriz que substrae

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ SubAssig() [3/3]

bool Pds::Matrix::SubAssig	(	double	beta,
		const Pds::Matrix &	B
	)

Resta y acumula en si mismo (A), una matriz B. Este es similar al operador -=.

$A \leftarrow A-\beta B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
B.Fill(1.0);
A.SubAssig(2,B);

Parámetros

[in]	beta	El factor a multiplicar.
[in]	B	La matriz que substrae

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ operator+=() [1/2]

Pds::Matrix & Pds::Matrix::operator+= ( double b )

Suma y acumula en si mismo (A), un valor b. Este operador es similar al método AddAssig()

$A \leftarrow A+b$

Pds::Matrix A(4,4);
double b=1.2;
A+=b;

Parámetros

[in] b El valor a acumular

Devuelve: Retorna el operador de la izquierda (acumulador) con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: AddAssig

◆ operator+=() [2/2]

Pds::Matrix & Pds::Matrix::operator+= ( const Pds::Matrix & B )

Suma y acumula en si mismo (A), una matriz B. Este operador es similar al método AddAssig()

$A \leftarrow A+B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
B.Fill(1.0);
A+=B;

Parámetros

[in] B la matriz a acumular

Devuelve: Retorna el operador de la izquierda (acumulador) con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: AddAssig

◆ AddAssig() [1/5]

bool Pds::Matrix::AddAssig ( double b )

Suma y acumula en si mismo (A), un valor b. Este es similar al perador +=.

$A \leftarrow A+b$

Pds::Matrix A(4,4);

A.AddAssig(1.2);

Parámetros

[in] b Valor a acumular

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ AddAssig() [2/5]

bool Pds::Matrix::AddAssig ( const Pds::Matrix & B )

Suma y acumula en si mismo (A), una matriz B. Este es similar al perador +=.

$A \leftarrow A+B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
B.Fill(1.0);
A.AddAssig(B);

Parámetros

[in] B la matriz a acumular

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ AddAssigColMatrix()

bool Pds::Matrix::AddAssigColMatrix ( const Pds::Matrix & B )

Suma y acumula en si mismo (A) e en cada columna, una matriz columna B.

$A \leftarrow A+B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,1);
B.Fill(1.0);
A.AddAssigColMatrix(B);

Parámetros

[in] B la matriz a acumular

Devuelve: Retorna true si todo fue bien o false si no. Retorna false si B no es una matriz columna. Si se retorna false el acumulador no altera su contenido.

◆ AddAssig() [3/5]

bool Pds::Matrix::AddAssig	(	double	alpha,
		const Pds::Matrix &	B
	)

Suma y acumula en si mismo (A), una matriz B.

$A \leftarrow A+\alpha B$

Pds::Matrix A(4,4);
double alpha=1.2;
Pds::Matrix B(4,4);
B.Fill(1.0);
A.AddAssig(alpha,B);

Parámetros

[in]	alpha	Factor a acumular
[in]	B	la matriz a acumular

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ AddAssig() [4/5]

bool Pds::Matrix::AddAssig	(	double	alpha,
		double	beta,
		const Pds::Matrix &	B
	)

Suma y acumula en si mismo (A), una matriz B.

$A \leftarrow \alpha A+\beta B$

Pds::Matrix A(4,4);
double alpha=0.8;
double beta=0.2;
Pds::Matrix B(4,4);
B.Fill(1.0);
A.AddAssig(alpha,beta,B);

Parámetros

[in]	alpha	Factor a acumular
[in]	beta	Factor a acumular
[in]	B	la matriz a acumular

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ AddAssig() [5/5]

bool Pds::Matrix::AddAssig	(	double	alpha,
		const Pds::Matrix &	B,
		double	beta,
		const Pds::Matrix &	C
	)

Suma y acumula en si mismo (A), una matriz B.

$A \leftarrow A+\alpha B+\beta C$

Pds::Matrix A(4,4);
double alpha=1.2;
Pds::Matrix B(4,4);
double beta=0.2;
Pds::Matrix C(4,4);
B.Fill(+1.0);   C.Fill(-1.0);
A.AddAssig(alpha,B,beta,C);

Parámetros

[in]	alpha	Factor a acumular
[in]	B	la matriz a acumular
[in]	beta	Factor a acumular
[in]	C	la matriz a acumular

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ AddAssigAt() [1/2]

bool Pds::Matrix::AddAssigAt	(	unsigned int	lin,
		unsigned int	col,
		const Pds::Matrix &	B
	)

Suma y acumula en si mismo (A), una matriz B desde un punto (lin,col) haciendo una intersección.

$A(lin:end,col:end) \leftarrow A(lin:end,col:end)+B(0:lin_end,0:col_end)$

Pds::Matrix A(4,4);
Pds::Matrix B(3,3);
B.Fill(1.0);
A.AddAssigAt(2,2,B);

Parámetros

[in]	lin	Suma desde esta linea
[in]	col	Suma desde esta columna
[in]	B	la matriz a acumular

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido. Retorna false si la intersección no existe o si alguna de las matrices son nulas.

Ejemplos: example_matrix_assignment.cpp.

◆ AddAssigAt() [2/2]

bool Pds::Matrix::AddAssigAt	(	unsigned int	lin,
		unsigned int	col,
		double	b
	)

Suma y acumula en si mismo (A), un valor b en un punto (lin,col)

$A(lin,col) \leftarrow A(lin,col)+b$

Pds::Matrix A(4,4);
double b=1;
A.AddAssigAt(2,2,b);

Parámetros

[in]	lin	Suma desde esta linea
[in]	col	Suma desde esta columna
[in]	b	Valor a acumular

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido. Retorna false si la matriz es nula o errores con lin y col.

◆ AddRawAssigAt()

void Pds::Matrix::AddRawAssigAt	(	unsigned int	lin,
		unsigned int	col,
		double	b
	)

inline

Suma y acumula en si mismo (A), un valor b en un punto (lin,col)

$A(lin,col) \leftarrow A(lin,col)+b$

Pds::Matrix A(4,4);
double b=1;
A.AddRawAssigAt(2,2,b);

Atención: No verifica si lin y col estan dentro del rango de la matriz, si está fuera de rango da error de acceso de memoria.

Parámetros

[in]	lin	Suma desde esta linea
[in]	col	Suma desde esta columna
[in]	b	Valor a acumular

Ejemplos: example_matrix_assignment.cpp.

Definición en la línea 7313 del archivo Matrix.hpp.

    {
        this->array[lin][col]=this->array[lin][col]+b;  
    }

◆ XorAssig()

bool Pds::Matrix::XorAssig	(	const Pds::Matrix &	B,
		double	Umbral = `0.5`
	)

Xor y acumula en si mismo (A), una matriz B.

$A \leftarrow A~xor~B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
A.FillRandC(0.5);
B.FillRandC(0.5);
A.XorAssig(B);

Parámetros

[in]	B	la matriz a acumular
[in]	Umbral	Umbral para binarizar ambas regiones a aplicar Xor.

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido. Retorna false si las matrices son de tamaños diferentes.

Ejemplos: example_matrix_assignment_bin.cpp.

◆ XorAssigAt()

bool Pds::Matrix::XorAssigAt	(	unsigned int	lin,
		unsigned int	col,
		const Pds::Matrix &	B,
		double	Umbral = `0.5`
	)

Xor y acumula en si mismo (A), una matriz B desde un punto (lin,col) haciendo una intersección.

$A(lin:end,col:end) \leftarrow A(lin:end,col:end)~xor~B(0:lin_end,0:col_end)$

Pds::Matrix A(4,4);
Pds::Matrix B(3,3);
B.Fill(1.0);
A.XorAssigAt(1,1,B);

Parámetros

[in]	lin	Suma desde esta linea
[in]	col	Suma desde esta columna
[in]	B	la matriz a acumular
[in]	Umbral	Umbral para binarizar ambas regiones a aplicar Xor.

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido. Retorna false si la intersección no existe o si alguna de las matrices son nulas.

Ejemplos: example_matrix_assignment_bin.cpp.

◆ OrAssigAt()

bool Pds::Matrix::OrAssigAt	(	unsigned int	lin,
		unsigned int	col,
		const Pds::Matrix &	B,
		double	Umbral = `0.5`
	)

Or y acumula en si mismo (A), una matriz B desde un punto (lin,col) haciendo una intersección.

$A(lin:end,col:end) \leftarrow A(lin:end,col:end)~or~B(0:lin_end,0:col_end)$

Pds::Matrix A(4,4);
Pds::Matrix B(3,3);
B.Fill(1.0);
A.OrAssigAt(1,1,B);

Parámetros

[in]	lin	Suma desde esta linea
[in]	col	Suma desde esta columna
[in]	B	la matriz a acumular
[in]	Umbral	Umbral para binarizar ambas regiones a aplicar Or.

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido. Retorna false si la intersección no existe o si alguna de las matrices son nulas.

Ejemplos: example_matrix_assignment_bin.cpp.

◆ AndAssigAt()

bool Pds::Matrix::AndAssigAt	(	unsigned int	lin,
		unsigned int	col,
		const Pds::Matrix &	B,
		double	Umbral = `0.5`
	)

And y acumula en si mismo (A), una matriz B desde un punto (lin,col) haciendo una intersección.

$A(lin:end,col:end) \leftarrow A(lin:end,col:end)~and~B(0:lin_end,0:col_end)$

Pds::Matrix A(4,4);
Pds::Matrix B(3,3);
B.Fill(1.0);
A.AndAssigAt(1,1,B);

Parámetros

[in]	lin	Suma desde esta linea
[in]	col	Suma desde esta columna
[in]	B	la matriz a acumular
[in]	Umbral	Umbral para binarizar ambas regiones a aplicar And.

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido. Retorna false si la intersección no existe o si alguna de las matrices son nulas.

Ejemplos: example_matrix_assignment_bin.cpp.

◆ XorAssigVectorAtCol()

bool Pds::Matrix::XorAssigVectorAtCol	(	unsigned int	col,
		const Pds::Vector &	B,
		double	Umbral = `0.5`
	)

Xor y acumula en si mismo (A), una matriz B desde un punto (0,col) haciendo una intersección.

$A(0:end,col) \leftarrow A(0:end,col)~xor~B(0:lin_end,0)$

Pds::Matrix A(4,4);
Pds::Matrix V(3);
B.FillRandC(0.5);
A.XorAssigAt(1,B);

Parámetros

[in]	col	Xor desde esta columna
[in]	B	El vector a Xor
[in]	Umbral	Umbral para binarizar ambas regiones a aplicar Xor.

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido. Retorna false si la intersección no existe o si alguna de las matrices son nulas.

Ejemplos: example_matrix_assignment_bin.cpp.

◆ ProductAssig() [1/3]

bool Pds::Matrix::ProductAssig ( double b )

Multiplica con sigo mismo (A), un valor b y el resultado es cargado en A.

$A \leftarrow b~A$

Pds::Matrix A(4,4);
double b=3;
 
A.Fill(2.0);
 
A.ProductAssig(b);
 
std::cout<<A;

Parámetros

[in] b El valor a multiplicar.

Devuelve: true si todo fue bien o false en caso de error.

◆ ProductAssig() [2/3]

bool Pds::Matrix::ProductAssig ( const Pds::Matrix & B )

[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz B y el resultado es cargado en A.

$A \leftarrow A\& B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
 
A.Fill(2.0);
B.Fill(1.0);
 
A.ProductAssig(B);
 
std::cout<<A;

Parámetros

[in] B la matriz a multiplicar.

Devuelve: true si todo fue bien o false en caso de error.

◆ ProductAssig() [3/3]

bool Pds::Matrix::ProductAssig	(	double(*)(double)	func,
		const Pds::Matrix &	B
	)

[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz func(B) y el resultado es cargado en A.

$A \leftarrow A\& func(B)$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
 
A.Fill(2.0);
B.Fill(1.0);
 
A.ProductAssig(func,B);
 
std::cout<<A;

Parámetros

[in]	func	Función a evaluar.
[in]	B	la matriz a multiplicar.

Devuelve: true si todo fue bien o false en caso de error.

◆ ProductAssigMinus() [1/2]

bool Pds::Matrix::ProductAssigMinus	(	double	b,
		const Pds::Matrix &	B
	)

[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz (b-B) y el resultado es cargado en A.

$A \leftarrow A\& (b-B)$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
 
A.Fill(2.0);
B.Fill(1.0);
 
A.ProductAssigMinus(1,B);
 
std::cout<<A;

Parámetros

[in]	b	La variable a multiplicar.
[in]	B	La matriz a multiplicar.

Devuelve: true si todo fue bien o false en caso de error.

◆ ProductAssigMinus() [2/2]

bool Pds::Matrix::ProductAssigMinus	(	const Pds::Matrix &	B,
		double	b
	)

[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz (B-b) y el resultado es cargado en A.

$A \leftarrow A\& (B-b)$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
 
A.Fill(2.0);
B.Fill(1.0);
 
A.ProductAssigMinus(B,1);
 
std::cout<<A;

Parámetros

[in]	B	La matriz a multiplicar.
[in]	b	La variable a multiplicar.

Devuelve: true si todo fue bien o false en caso de error.

◆ ProductAssigPlus()

bool Pds::Matrix::ProductAssigPlus	(	double	b,
		const Pds::Matrix &	B
	)

[Elemento a elemento] Multiplica con sigo mismo (A), elemento a elemento, una matriz (b+B) y el resultado es cargado en A.

$A \leftarrow A\& (b+B)$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
 
A.Fill(2.0);
B.Fill(1.0);
 
A.ProductAssigMinus(1,B);
 
std::cout<<A;

Parámetros

[in]	b	La variable a multiplicar.
[in]	B	La matriz a multiplicar.

Devuelve: true si todo fue bien o false en caso de error.

◆ operator*=() [1/2]

Pds::Matrix & Pds::Matrix::operator*= ( double b )

Multiplica y acumula en si mismo (A), un valor b. Este operador es similar al método MulAssig()

$A \leftarrow A*b$

Pds::Matrix A(4,4);
double b=1.2;
A*=b;

Parámetros

[in] b El valor a acumular

Devuelve: Retorna el operador de la izquierda (acumulador) con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: AddAssig

◆ operator*=() [2/2]

Pds::Matrix & Pds::Matrix::operator*= ( const Pds::Matrix & B )

Multiplica y acumula en si mismo (A), una matriz B. Este operador es similar al método MulAssig()

$A \leftarrow A*B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
A*=B;

Parámetros

[in] B El valor a acumular

Devuelve: Retorna el operador de la izquierda (acumulador) con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: AddAssig

◆ MulAssig() [1/2]

bool Pds::Matrix::MulAssig ( double b )

Multiplica y acumula en si mismo (A), un valor b. Este es similar al operador *=.

$A \leftarrow A*b$

Pds::Matrix A(4,4);

A.MulAssig(1.2);

Parámetros

[in] b Valor a acumular

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ MulAssig() [2/2]

bool Pds::Matrix::MulAssig ( const Pds::Matrix & B )

Multiplica y acumula en si mismo (A), una matriz B. Este es similar al operador *=.

$A \leftarrow A*B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
A.MulAssig(B);

Parámetros

[in] B Valor a acumular

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ operator/=()

Pds::Matrix & Pds::Matrix::operator/= ( const Pds::Matrix & B )

[Elemento a elemento] Divide y acumula en si mismo (A), una matriz B. Este operador es similar al método DivAssig()

$A \leftarrow A/B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
A/=B;

Parámetros

[in] B El valor a acumular

Devuelve: Retorna el operador de la izquierda (acumulador) con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: DivAssig

◆ DivAssig()

bool Pds::Matrix::DivAssig ( const Pds::Matrix & B )

Divide y acumula en si mismo (A), una matriz B. Este es similar al operador /=.

$A \leftarrow A/B$

Pds::Matrix A(4,4);
Pds::Matrix B(4,4);
A.DivAssig(B);

Parámetros

[in] B Valor a acumular

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ DivBelowAssig()

bool Pds::Matrix::DivBelowAssig ( double b )

[Elemento a elemento] Divide y acumula en si mismo (A), un valor b.

$A \leftarrow b/A$

Pds::Matrix A(4,4);

A.DivBelowAssig(1.0);

Parámetros

[in] b Valor a usar.

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el acumulador no altera su contenido.

◆ operator=() [1/3]

Pds::Matrix & Pds::Matrix::operator= ( const Pds::Matrix & B )

Copia en si mismo (A), una matriz B. Este operador es similar al método Copy(). No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos es reservado.

$A \leftarrow B$

Cuando acontece:

Pds::Matrix B(nlin,ncol);

A=B;

Pds::Matrix::nlin

unsigned int nlin

Definition: Matrix.hpp:101

Pds::Matrix::ncol

unsigned int ncol

Definition: Matrix.hpp:103

Cuando NO acontece:

Pds::Matrix A=Pds::Matrix(nlin,ncol);

Pds::Ra::Tag::Matrix

const std::string Matrix

Tag de un objeto de tipo Pds::Ra::Tag::Matrix.

Definition: RaDefines.hpp:402

Parámetros

[in] B la matriz a copiar

Devuelve: Retorna el operador de la izquierda (acumulador) con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: Copy

◆ Copy() [1/3]

bool Pds::Matrix::Copy ( const Pds::Matrix & B )

Copia en si mismo (A), el contenido de una matriz B. Este método es similar a usar el operador = . No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos es reservado.

$A \leftarrow B$

Parámetros

[in] B la matriz a copiar

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el receptor no altera su contenido.

Ver también: Copy

◆ operator=() [2/3]

Pds::Matrix & Pds::Matrix::operator= ( double val )

Copia en si mismo (A), el valor val. Este operador es similar al método Copy(). No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos de 1x1 es reservado.

$A \leftarrow val$

Cuando acontece:

Pds::Matrix B(nlin,ncol);

A=val;

Cuando NO acontece:

Pds::Matrix A=Pds::Matrix(nlin,ncol);

Parámetros

[in] val El valor a copiar

Devuelve: Retorna el operador de la izquierda (acumulador) con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: Copy

◆ Copy() [2/3]

bool Pds::Matrix::Copy ( double val )

Copia en si mismo (A), el valor val. Este método es similar a usar el operador = . No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos de 1x1 es reservado.

$A \leftarrow val$

Parámetros

[in] val El valor a copiar

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el receptor no altera su contenido.

Ver también: Copy

◆ operator=() [3/3]

template<class Datum >

Pds::Matrix & Pds::Matrix::operator= ( const Pds::Array< Datum > & B )

Copia en si mismo (A), una array B. Este operador es similar al método Copy(). No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos es reservado.

$A \leftarrow B$

Cuando acontece:

Pds::Matrix A;
Pds::Array<double> B(nlin,ncol);
A=B;

Parámetros

[in] B El array a copiar

Devuelve: Retorna el operador de la izquierda (acumulador) con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: Copy

◆ Copy() [3/3]

template<class Datum >

bool Pds::Matrix::Copy ( const Pds::Array< Datum > & B )

Copia en si mismo (A), el contenido de una Array B. Este método es similar a usar el operador = . No importa el tamaño de A, sus datos son liberados y un nuevo arreglo de datos es reservado.

$A \leftarrow B$

Parámetros

[in] B la matriz a copiar

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el receptor no altera su contenido.

◆ KNearest() [1/2]

std::vector< unsigned int > Pds::Matrix::KNearest	(	unsigned int	K,
		const Pds::Vector &	V,
		std::vector< double > &	D2
	)		const

Calcula que linea de $\mathbf{C}\in \mathbb{R}^{M\times N}$ es mas cercana al vector $\mathbf{v}\in \mathbb{R}^{N}$ .

$\mathbf{id}= \begin{bmatrix} id_0\\ id_1\\ \vdots\\ id_k\\ \vdots\\ id_{K-1}\\ \end{bmatrix}, \quad \mathbf{d}^{2}= \begin{bmatrix} d^{2}_0\\ d^{2}_1\\ \vdots\\ d^{2}_k\\ \vdots\\ d^{2}_{K-1}\\ \end{bmatrix} \quad \leftarrow \quad \mathbf{C}= \begin{bmatrix} \mathbf{c}_0^{T}\\ \mathbf{c}_1^{T}\\ \vdots\\ \mathbf{c}_m^{T}\\ \vdots\\ \mathbf{c}_{M-1}^{T}\\ \end{bmatrix}, \qquad \mathbf{v}= \begin{bmatrix} x_0\\ x_1\\ \vdots\\ x_n\\ \vdots\\ x_{N-1}\\ \end{bmatrix}$

$d^{2}_{m}=\sum_{n}^{N}|c_{mn}-x_{n}|^2$

$id_{k}=\arg\min_{m,<k>}{d^{2}_{m}}$

std::vector<unsigned int> ID;
std::vector<double> D2;
ID=C.KNearest(K,V,D2)

El vector $\mathbf{id}$ contiene a los indices de las lineas de $\mathbf{C}$ que estan mas cerca al vector $\mathbf{v}$ . Las lineas son comparadas usando distancia euclidiana al cuadrado.

Parámetros

[in]	K	Número máximo de vecinos a buscar.
[in]	V	Vector $\mathbf{v}$ a comparar. C.Ncol() debe ser igual V.Nel().
[out]	D2	El vector $\mathbf{d}^{2}$ de las distancias euclidianas al cuadrado correspondientes a $\mathbf{id}$ .

Devuelve: Retorna un vector entero $ID\equiv \mathbf{id}$ , de elementos. El primer elemento es el mas cercano. En caso de que el vector $\mathbf{v}$ sea vacío se retorna un vector vazio.

Ejemplos: example_matrix_knearest.cpp.

◆ KNearest() [2/2]

std::vector< unsigned int > Pds::Matrix::KNearest	(	unsigned int	K,
		const Pds::Vector &	V
	)		const

Calcula que linea de $\mathbf{C}\in \mathbb{R}^{M\times N}$ es mas cercana al vector $\mathbf{v}\in \mathbb{R}^{N}$ .

$\mathbf{id}= \begin{bmatrix} id_0\\ id_1\\ \vdots\\ id_k\\ \vdots\\ id_{K-1}\\ \end{bmatrix} \quad \leftarrow \quad \mathbf{C}= \begin{bmatrix} \mathbf{c}_0^{T}\\ \mathbf{c}_1^{T}\\ \vdots\\ \mathbf{c}_m^{T}\\ \vdots\\ \mathbf{c}_{M-1}^{T}\\ \end{bmatrix}, \qquad \mathbf{v}= \begin{bmatrix} x_0\\ x_1\\ \vdots\\ x_n\\ \vdots\\ x_{N-1}\\ \end{bmatrix}$

$d^{2}_{m}=\sum_{n}^{N}|c_{mn}-x_{n}|^2$

$id_{k}=\arg\min_{m,<k>}{d^{2}_{m}}$

std::vector<unsigned int> ID;

ID=C.KNearest(K,V)

El vector $\mathbf{id}$ contiene a los indices de las lineas de $\mathbf{C}$ que estan mas cerca al vector $\mathbf{v}$ . Las lineas son comparadas usando distancia euclidiana al cuadrado.

Parámetros

[in]	K	Número máximo de vecinos a buscar.
[in]	V	Vector $\mathbf{v}$ a comparar. C.Ncol() debe ser igual V.Nel().

Devuelve: Retorna un vector entero $ID\equiv \mathbf{id}$ , de elementos. El primer elemento es el mas cercano. En caso de que el vector $\mathbf{v}$ sea vacío se retorna un vector vazio.

◆ IdInMultipleMse() [1/2]

Pds::Array< unsigned int > Pds::Matrix::IdInMultipleMse ( const Pds::Matrix & X ) const

Calcula que linea de $\mathbf{C}$ es mas cercana a cada linea de $\mathbf{X}\in \mathbb{R}^{L\times N}$ .

$\mathbf{id}= \begin{bmatrix} id_0\\ id_1\\ \vdots\\ id_l\\ \vdots\\ id_{L-1}\\ \end{bmatrix} \quad \leftarrow \quad \mathbf{C}= \begin{bmatrix} \mathbf{c}_0^{T}\\ \mathbf{c}_1^{T}\\ \vdots\\ \mathbf{c}_m^{T}\\ \vdots\\ \mathbf{c}_{M-1}^{T}\\ \end{bmatrix}, \qquad \mathbf{X}= \begin{bmatrix} \mathbf{x}_0^{T}\\ \mathbf{x}_1^{T}\\ \vdots\\ \mathbf{x}_l^{T}\\ \vdots\\ \mathbf{x}_{L-1}^{T}\\ \end{bmatrix}$

$id_{l}=\arg\min_{m}{\sum_{n}^{N}\frac{|c_{mn}-x_{ln}|^2}{N}}$

ID=C.IdInMultipleMse(X)

El elemento $id_{l}$ contiene la linea de $\mathbf{C}$ que esta mas cercana a la linea de $\mathbf{X}$ . Las lineas son comparadas usando distancia euclidiana.

Parámetros

[in] X Matriz a comparar. C.Ncol() debe ser igual X.Ncol().

Devuelve: Retorna una matriz entera $ID\equiv \mathbf{id}$ , de lineas y 1 columna. Cada linea de $\mathbf{id}$ contiene el indice de la linea de $\mathbf{C}$ que es mas cercana a cada linea de $\mathbf{X}$ . En caso de que la matriz sea vacía se retorna una matriz vazia

Ejemplos: example_matrix_algebra.cpp.

◆ IdInMultipleMse() [2/2]

Pds::Array< unsigned int > Pds::Matrix::IdInMultipleMse ( const std::vector< Pds::Matrix > & Block ) const

Calcula que linea de $\mathbf{C}$ es mas cercana a cada muestra $0 \leq (lin,col)< (Nlin, Ncol)$ en el bloque $\mathbf{Block}\in \mathbb{R}^{N\times Nlin\times Ncol}$ .

$\mathbf{C}= \begin{bmatrix} \mathbf{c}_0^{T}\\ \mathbf{c}_1^{T}\\ \vdots\\ \mathbf{c}_m^{T}\\ \vdots\\ \mathbf{c}_{M-1}^{T}\\ \end{bmatrix}, \qquad \mathbf{Block}= \begin{bmatrix} \mathbf{block}[0]& \mathbf{block}[1]& \dots& \mathbf{block}[n]& \dots& \mathbf{block}[N-1] \end{bmatrix}$

La matriz $\mathbf{C}$ debe tener columnas y el bloque $\mathbf{Block}$ debe estar compuesto de matrices.

$id_{ij}=\arg\min_{m}{\sum_{n}^{N}\frac{|c_{mn}-block[n](i,j)|^2}{N}}$

ID=C.IdInMultipleMse(Block)

El elemento $id_{ij}$ constiene la linea de $\mathbf{C}$ que esta mas cercana a la muestra de $\mathbf{Block}$ . La lineas son comparadas usando distancia euclidiana.

Parámetros

[in] Block Bloque de matrices a comparar.

Devuelve: Retorna una matriz entera $\mathbf{ID}$ , de lineas y columnas. Cada elemento de $\mathbf{ID}$ contiene el indice de la linea de $\mathbf{C}$ que es mas cercanas a cada muestra de $\mathbf{Block}$ . En caso de que la matriz sea vacía se retorna una matriz vazia

◆ ArrayAllocate() [1/7]

static double ** Pds::Matrix::ArrayAllocate	(	double(*)(double)	func,
		const Pds::Matrix &	A
	)

static

crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A).

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double).
[in]	A	Matriz de donde se copiaran datos.

Devuelve: Retorna un puntero al arreglo, o NULL si no consiguió reservar la memoria. Esta memoria debe ser liberada siempre com ArrayRelease

◆ ArrayAllocate() [2/7]

static double ** Pds::Matrix::ArrayAllocate	(	double(*)(double, double)	func,
		const Pds::Matrix &	A,
		double	var
	)

static

crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,var).

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double).
[in]	A	Matriz de donde se copiaran datos.
[in]	var	Variable a evaluar.

Devuelve: Retorna un puntero al arreglo, o NULL si no consiguió reservar la memoria. Esta memoria debe ser liberada siempre com ArrayRelease

◆ ArrayAllocate() [3/7]

static double ** Pds::Matrix::ArrayAllocate	(	double(*)(double, double)	func,
		const Pds::Matrix &	A,
		const Pds::Matrix &	B
	)

static

crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,B). Los tamaño de A y B son similares.

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double,double).
[in]	A	Matriz de donde se copiaran datos.
[in]	B	Matriz de donde se copiaran datos.

Devuelve: Retorna un puntero al arreglo, o NULL si no consiguió reservar la memoria. Esta memoria debe ser liberada siempre com ArrayRelease

◆ ArrayAllocate() [4/7]

static double ** Pds::Matrix::ArrayAllocate	(	double(*)(double, double, double)	func,
		const Pds::Matrix &	A,
		const Pds::Matrix &	B,
		double	var
	)

static

crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,B,var). Los tamaño de A y B son similares.

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double,double,double).
[in]	A	Matriz de donde se copiaran datos.
[in]	B	Matriz de donde se copiaran datos.
[in]	var	Tercer valor a evaluar.

Devuelve: Retorna un puntero al arreglo, o NULL si no consiguió reservar la memoria. Esta memoria debe ser liberada siempre com ArrayRelease

◆ ArrayAllocate() [5/7]

static double ** Pds::Matrix::ArrayAllocate	(	double(*)(double, double, double)	func,
		const Pds::Matrix &	A,
		const Pds::Matrix &	B,
		const Pds::Matrix &	C
	)

static

crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,B,C). Los tamaño de A, B y C son similares.

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double,double,double).
[in]	A	Matriz de donde se copiaran datos.
[in]	B	Matriz de donde se copiaran datos.
[in]	C	Matriz de donde se copiaran datos.

Devuelve: Retorna un puntero al arreglo, o NULL si no consiguió reservar la memoria. Esta memoria debe ser liberada siempre com ArrayRelease

◆ ArrayAllocate() [6/7]

static double ** Pds::Matrix::ArrayAllocate	(	double(*)(double, double, double, double)	func,
		const Pds::Matrix &	A,
		const Pds::Matrix &	B,
		const Pds::Matrix &	C,
		double	var
	)

static

crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,B,C,var). Los tamaño de A, B y C son similares.

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double,double,double,double).
[in]	A	Matriz de donde se copiaran datos.
[in]	B	Matriz de donde se copiaran datos.
[in]	C	Matriz de donde se copiaran datos.
[in]	var	Cuarto valor a evaluar.

Devuelve: Retorna un puntero al arreglo, o NULL si no consiguió reservar la memoria. Esta memoria debe ser liberada siempre com ArrayRelease

◆ ArrayAllocate() [7/7]

static double ** Pds::Matrix::ArrayAllocate	(	double(*)(double, double, double, double)	func,
		const Pds::Matrix &	A,
		const Pds::Matrix &	B,
		const Pds::Matrix &	C,
		const Pds::Matrix &	D
	)

static

crea dinámicamente un arreglo de A.Nlin() lineas y A.Ncol() columnas, con los datos copiados de aplicar func(A,B,C,D). Los tamaño de A, B, C y D son similares.

Parámetros

[in]	func	Función a aplicar, esta debe tener a forma double func(double,double,double,double).
[in]	A	Matriz de donde se copiaran datos.
[in]	B	Matriz de donde se copiaran datos.
[in]	C	Matriz de donde se copiaran datos.
[in]	D	Matriz de donde se copiaran datos.

Devuelve: Retorna un puntero al arreglo, o NULL si no consiguió reservar la memoria. Esta memoria debe ser liberada siempre com ArrayRelease

◆ operator<<()

std::ostream & operator<<	(	std::ostream &	out,
		const Pds::Matrix &	mat
	)

Retorna el contenido de la matriz por la salida estándar.

std::cout<<mat;

es equivalente a :

std::cout<<mat.ToString();

Parámetros

[in]	out	La salida
[in]	mat	La matriz a mostrar

Devuelve: Retorna la misma salida estándar out.

Ver también: Pds::Matrix::ToString();

◆ operator+() [4/4]

Pds::Matrix operator+	(	double	b,
		const Pds::Matrix &	A
	)

Suma b con (A), el resultado es cargado en C. Este operador es similar al método Add()

$C \leftarrow b+A$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=2.0+A;
 
std::cout<<C;

Parámetros

[in]	b	El valor a sumar
[in]	A	matriz a sumar

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: Add

◆ operator-() [4/4]

Pds::Matrix operator-	(	double	b,
		const Pds::Matrix &	A
	)

Resta b con (A), el resultado es cargado en C. Este operador es similar al método Add()

$C \leftarrow b-A$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=2.0-A;
 
std::cout<<C;

Parámetros

[in]	b	El valor a operar
[in]	A	matriz a restar

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: Sub

◆ operator*() [3/3]

Pds::Matrix operator*	(	double	b,
		const Pds::Matrix &	A
	)

Multiplica b con (A), el resultado es cargado en C. Este operador es similar al método Mul()

$C \leftarrow b*A$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=2.0*A;
 
std::cout<<C;

Parámetros

[in]	b	El valor a operar
[in]	A	matriz a multiplicar

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: Mul

◆ operator/() [3/3]

Pds::Matrix operator/	(	double	b,
		const Pds::Matrix &	A
	)

Divide b con (A), elemento a elemento y el resultado es cargado en C. Este operador es similar al método DivSelf()

$C \leftarrow b/A$

Pds::Matrix A(4,4);
Pds::Matrix C;
 
A.Fill(2.0);
 
C=2.0/A;
 
std::cout<<C;

Parámetros

[in]	b	El valor a operar
[in]	A	matriz a dividir

Devuelve: Retorna un nuevo objeto con el resultado, o una matriz vacía (this->IsEmpty() igual a true) en caso de error.

Ver también: Mul

◆ ~Matrix()

Pds::Matrix::~Matrix ( )

Namespaces

Estructuras de datos

typedefs

Constructores

Métodos de estado

Métodos de inicialización

Métodos de tamaño

Métodos get y set de elementos

Métodos get y set de matrices y vectores

Métodos de opreaciones sobre las lineas de la matriz

Métodos estadísticos

Métodos Information theory

Métodos Digital Signal Processing

Métodos de álgebra lineal

Métodos de álgebra lineal - Eigenvalues Eigenvectors

Métodos para find

Métodos para aplicar operaciones

Métodos para operar Pds::Matrix

Métodos con regiones con Pds::Matrix.

Métodos variados con Pds::Matrix.

Métodos para reordenar memoria con Pds::Matrix.

Métodos para exportar e importar TXT con Pds::Matrix.

Métodos para exportar e importar CSV con Pds::Matrix.

Métodos para exportar e importar TEX con Pds::Matrix.

Métodos para exportar e importar Json con Pds::Matrix.

Métodos para exportar e importar XML con Pds::Matrix.

Métodos para exportar en formato Octave/Matlab desde Pds::Matrix.

Métodos para exportar e importar BMP con Pds::Matrix.

Métodos Static con procesamiento de 3 matrices.

Métodos Static con Matrices SampleBlock.

Métodos Static con Matrices BatchBlock.

Métodos Static con Matrices extras.

Operadores unarios y sus métodos equivalentes con Pds::Matrix.

Operadores binarios y sus métodos equivalentes con Pds::Matrix.

Operadores binarios acumuladores y sus métodos equivalentes con Pds::Matrix.

Métodos para calculo de kmeans y centroides con Pds::Matrix

Métodos Static con arrays

Operadores no miembros

Descripción detallada

Documentación de los 'typedefs'

◆ SampleBlock

◆ BatchBlock

Documentación de las funciones

◆ Matrix() [1/23]

◆ Matrix() [2/23]

◆ Matrix() [3/23]

◆ Matrix() [4/23]

◆ Matrix() [5/23]

◆ Matrix() [6/23]

◆ Matrix() [7/23]

◆ Matrix() [8/23]

◆ Matrix() [9/23]

◆ Matrix() [10/23]

◆ Matrix() [11/23]

◆ Matrix() [12/23]

◆ Matrix() [13/23]

◆ Matrix() [14/23]

◆ Matrix() [15/23]

◆ Matrix() [16/23]

◆ Matrix() [17/23]

◆ Matrix() [18/23]

◆ Matrix() [19/23]

◆ Matrix() [20/23]

◆ Matrix() [21/23]

◆ Matrix() [22/23]

◆ Matrix() [23/23]

◆ IsEmpty()

◆ IsNotEmpty()

◆ IsSimilarTo()

◆ IsNotSimilarTo()

◆ IsMulBy()

◆ IsNotMulBy()

◆ IsInRange()

◆ IsNotInRange()

◆ IsInSizeRange()

◆ IsRowMatrix()

◆ IsColMatrix()

◆ IsZero()

◆ IsLeq() [1/2]

◆ IsLeq() [2/2]