Funciones para trabajar con "Clustering": Pds::Clustering::GMM(), etc. Más...

Namespaces
namespace	Pds
	Nombre de espacio para Pds (Procesamiento Digital de Senales)

namespace	Pds::Clustering
	Nombre de espacio para Clustering.

Clustering : Gaussiam mixture model
Pds::DataGMM	Pds::Clustering::GMM (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::DataGMM &In)
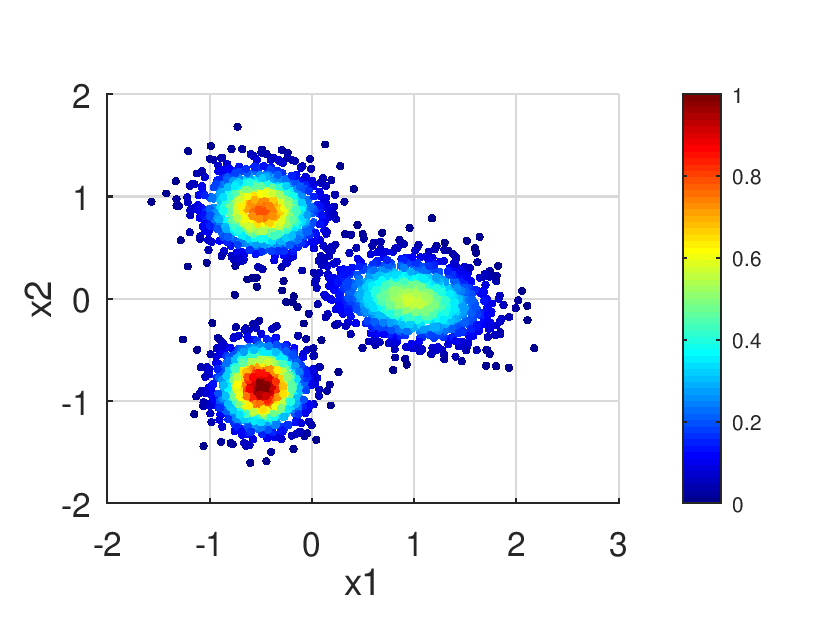
	Itera un Gaussian Mixture Model (GMM) [1] (pp. 13). Tenemos como conocimiento de estrada, valores iniciales 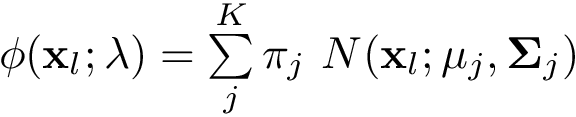$\lambda=\{\pi_k,\mu_k,\Sigma_k\}\qquad k=0,1,...,K-1$ de grupos de parametros para la función de densidad de probabilidad $\phi(\mathbf{x}_l;\lambda) =\sum\limits_{j}^K\pi_j~ N(\mathbf{x}_l;\mathbf{\mu}_j,\mathbf{\Sigma}_j)$ . Más...

Pds::DataGMM	Pds::Clustering::GMM (Pds::IterationConf &Conf, const Pds::Matrix &X, unsigned int K, double Sigma)
	Itera un Gaussian Mixture Model (GMM) [1] (pp. 13). Tenemos como conocimiento de estrada, valores iniciales 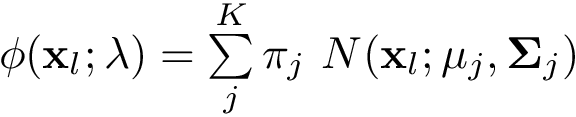$\lambda=\{\pi_k,\mu_k,\Sigma_k\}\qquad k=0,1,...,K-1$ de grupos de parametros para la función de densidad de probabilidad $\phi(\mathbf{x}_l;\lambda) =\sum\limits_{j}^K\pi_j~ N(\mathbf{x}_l;\mathbf{\mu}_j,\mathbf{\Sigma}_j)$ . Más...

Descripción detallada

Funciones para trabajar con "Clustering": Pds::Clustering::GMM(), etc.

#include <Pds/FuncClusteringGMM>

Documentación de las funciones

◆ GMM() [1/2]

Pds::DataGMM Pds::Clustering::GMM	(	Pds::IterationConf &	Conf,
		const Pds::Matrix &	X,
		const Pds::DataGMM &	In
	)

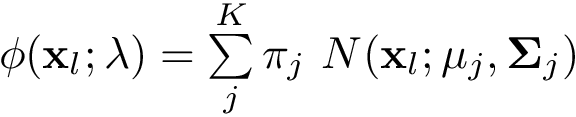Itera un Gaussian Mixture Model (GMM) [1] (pp. 13). Tenemos como conocimiento de estrada, valores iniciales $\lambda=\{\pi_k,\mu_k,\Sigma_k\}\qquad k=0,1,...,K-1$ de grupos de parametros para la función de densidad de probabilidad $\phi(\mathbf{x}_l;\lambda) =\sum\limits_{j}^K\pi_j~ N(\mathbf{x}_l;\mathbf{\mu}_j,\mathbf{\Sigma}_j)$ .

Los datos son calculados mediante las siguientes ecuaciones.

$N(\mathbf{x};\mathbf{\mu}_k,\mathbf{\Sigma}_k)= \frac{ \exp \left( -\frac {1}{2}({\mathbf{x}}-{\boldsymbol{\mu}_k})^{\mathrm {T}}{\boldsymbol{\Sigma}}_k^{-1}({\mathbf {x} }-{\boldsymbol{\mu}_k}) \right) }{\sqrt {(2\pi )^{N}|{\boldsymbol{\Sigma}_k}|}}$

Hacer:

$\begin{array}{ll} \gamma_{k}(\mathbf{x}_l) & = \frac{\pi_k~ N(\mathbf{x}_l;\mathbf{\mu}_k,\mathbf{\Sigma}_k)}{\phi(\mathbf{x}_l;\lambda)}\\ \phi(\mathbf{x}_l;\lambda)&=\sum\limits_{j}^K\pi_j~ N(\mathbf{x}_l;\mathbf{\mu}_j,\mathbf{\Sigma}_j)\\ N_k & =\sum\limits_{l}^{L}\gamma_{k}(\mathbf{x}_l)\\ ~ & ~\\ \{\pi_k\}_{new} & =\frac{N_k}{L}\\ \{\mu_k\}_{new} &=\frac{1}{N_k}\sum\limits_{l}^{L}\gamma_{k}(\mathbf{x}_l) ~ \mathbf{x}_l\\ \{\Sigma_k\}_{new} & =\frac{1}{N_k}\sum\limits_{l}^{L}\gamma_{k}(\mathbf{x}_l) ~ (\mathbf{x}_l-\mathbf{\mu}_k) (\mathbf{x}_l-\mathbf{\mu}_k)^T \end{array}$

Mientras 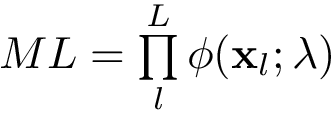$ML= \prod\limits_{l}^{L} \phi(\mathbf{x}_l;\lambda)$ no converge. $\frac{|log(ML)-log(ML)_{last}|}{|log(ML)|}<MinError$

Atención: La función $\phi(\mathbf{x};\lambda)$ es equivalente a la función Pds::Probability::GMMDensity().

Pds::Probability::GMMDensity()

Si se desea realizar clustering se recomienda usar Prob=Pds::Probability::GMMPartial(...); ID=Prob.OperateRows(Pds::ArgMax);

Parámetros

[in]	Conf	Configuracion de las iteraciones.
[in]	X	Matriz con los vectores de datos (muestras) en las lineas.
[in]	In	Datos iniciales $\lambda=\{\pi_k,\mu_k,\Sigma_k\}\qquad k=0,1,...,K-1$ de una estructura de datos tipo Pds::DataGMM con los datos de las gaussianas

Devuelve: Retorna una estructura de datos $\lambda=\{\pi_k,\mu_k,\Sigma_k\}\qquad k=0,1,...,K-1$ de tipo Pds::DataGMM que puede ser usada en la función $\phi(\mathbf{x};\lambda)$ la cual es equivalente a la función Pds::Probability::GMMDensity().

Ejemplos: example_funcgmm_probability.cpp y example_perceptron_kernel_gaussian_gmm.cpp.

◆ GMM() [2/2]

Pds::DataGMM Pds::Clustering::GMM	(	Pds::IterationConf &	Conf,
		const Pds::Matrix &	X,
		unsigned int	K,
		double	Sigma
	)

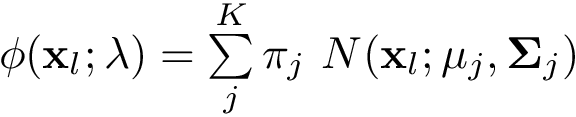Itera un Gaussian Mixture Model (GMM) [1] (pp. 13). Tenemos como conocimiento de estrada, valores iniciales $\lambda=\{\pi_k,\mu_k,\Sigma_k\}\qquad k=0,1,...,K-1$ de grupos de parametros para la función de densidad de probabilidad $\phi(\mathbf{x}_l;\lambda) =\sum\limits_{j}^K\pi_j~ N(\mathbf{x}_l;\mathbf{\mu}_j,\mathbf{\Sigma}_j)$ .

Pds::DataGMM Dat;
 
ID=Pds::Ra::IndicesRandVector(0,X.Nlin()-1,K);
Pds::Matrix I=Pds::Eye(X.Ncol());
 
for(unsigned int k=0;k<K;k++)
{
     Dat.Pi.push_back(1.0/K);
     Dat.Mu.push_back(X.GetRowAsColVector(ID[k]));
     Dat.Sinv.push_back(I/Sigma);
}
 
Pds::Clustering::GMM(Conf,X,Dat);

Atención: La función $\phi(\mathbf{x};\lambda)$ es equivalente a la función Pds::Probability::GMMDensity().

Pds::Probability::GMMDensity()

Si se desea realizar clustering se recomienda usar Prob=Pds::Probability::GMMPartial(...); ID=Prob.OperateRows(Pds::ArgMax);

Parámetros

[in]	Conf	Configuracion de las iteraciones.
[in]	X	Matriz con los vectores de datos (muestras) en las lineas.
[in]	K	Número de clusters.
[in]	Sigma	Desvio padron inicial de los clasters.

Devuelve: Retorna una estructura de datos $\lambda=\{\pi_k,\mu_k,\Sigma_k\}\qquad k=0,1,...,K-1$ de tipo Pds::DataGMM que puede ser usada en la función $\phi(\mathbf{x};\lambda)$ la cual es equivalente a la función Pds::Probability::GMMDensity().

Namespaces

Clustering : Gaussiam mixture model

Descripción detallada

Documentación de las funciones

◆ GMM() [1/2]

◆ GMM() [2/2]

Enlaces de interés