 |

|
Funciones para trabajar con "Probability": Pds::Probability::MGaussian(), etc. Más...
Namespaces | |
| namespace | Pds |
| Nombre de espacio para Pds (Procesamiento Digital de Senales) | |
| namespace | Pds::Probability |
| Nombre de espacio para Probability. | |
Probability of Gaussian | |
| Pds::Vector | Pds::Probability::MGaussian (const Pds::Matrix &X, const Pds::Vector &Mu, const double &Sigma) |
| Evalua la "probability density function" | |
| Pds::Vector | Pds::Probability::MGaussian (const Pds::Matrix &X, const Pds::Vector &Mu, const Pds::Matrix &Sinv) |
| Evalua la "probability density function" | |
| Pds::Vector | Pds::Probability::MGaussian (const Pds::Matrix &X, const Pds::Vector &Mu, const Pds::Matrix &Sinv, double det) |
| Evalua la "probability density function" | |
Probability of Gaussian Mixture Model | |
| Pds::Vector | Pds::Probability::GMMDensity (const Pds::Matrix &X, const std::vector< double > &Pi, const std::vector< Pds::Vector > &Mu, const std::vector< Pds::Matrix > &Sinv) |
Retorna el vector 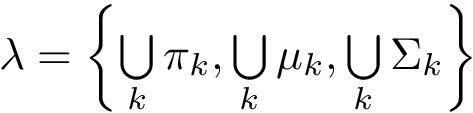 , donde , donde | |
| Pds::Vector | Pds::Probability::GMMDensity (const Pds::Matrix &X, const std::vector< double > &Pi, const std::vector< Pds::Vector > &Mu, const std::vector< Pds::Matrix > &Sinv, const std::vector< double > &Det) |
Retorna el vector 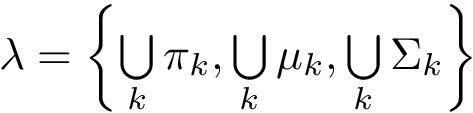 , donde , donde | |
| Pds::Vector | Pds::Probability::GMMDensity (const Pds::Matrix &X, const Pds::DataGMM &Dat) |
Retorna el vector 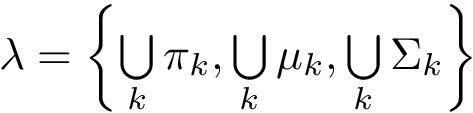 , donde , donde | |
| Pds::Matrix | Pds::Probability::GMMPartial (const Pds::Matrix &X, const std::vector< double > &Pi, const std::vector< Pds::Vector > &Mu, const std::vector< Pds::Matrix > &Sinv) |
| Retorna una Matriz | |
| Pds::Matrix | Pds::Probability::GMMPartial (const Pds::Matrix &X, const std::vector< double > &Pi, const std::vector< Pds::Vector > &Mu, const std::vector< Pds::Matrix > &Sinv, const std::vector< double > &Det) |
| Retorna una Matriz | |
| Pds::Matrix | Pds::Probability::GMMPartial (const Pds::Matrix &X, const Pds::DataGMM &Dat) |
| Retorna una Matriz | |
Probability of Parzen Window Classifier | |
| Pds::Vector | Pds::Probability::PWCDensity (const Pds::Matrix &X, const Pds::Matrix &C, const Pds::Matrix &Sinv, double h=0.1) |
| Retorna un vector | |
| Pds::Vector | Pds::Probability::PWCDensity (const Pds::Matrix &X, const Pds::Matrix &C, const Pds::Matrix &Sinv, double h, double det) |
| Retorna un vector | |
Funciones para trabajar con "Probability": Pds::Probability::MGaussian(), etc.
| Pds::Vector Pds::Probability::MGaussian | ( | const Pds::Matrix & | X, |
| const Pds::Vector & | Mu, | ||
| const double & | Sigma | ||
| ) |
Evalua la "probability density function" ![]() de la funcion gaussiana multivariada, usando
de la funcion gaussiana multivariada, usando ![]() , la variable
, la variable ![]() y
y ![]() .
.
![\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_{0}^T\\ \mathbf{x}_{1}^T\\ \vdots\\ \mathbf{x}_{l}^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) \qquad \rightarrow \qquad \mathbf{Y}= \left( \begin{matrix} p(\mathbf{x}_{0};\mathbf{\mu},\mathbf{\sigma})\\ p(\mathbf{x}_{1};\mathbf{\mu},\mathbf{\sigma})\\ \vdots\\ p(\mathbf{x}_{l};\mathbf{\mu},\mathbf{\sigma})\\ \vdots\\ p(\mathbf{x}_{L-1};\mathbf{\mu},\mathbf{\sigma})\\ \end{matrix} \right) \]](form_200.png)
![\[ p(\mathbf{x};\mathbf{\mu},\mathbf{\sigma})= \frac{ \exp \left( -\frac {1}{2 {\boldsymbol{\sigma }}^{2}}({\mathbf{x}}-{\boldsymbol{\mu}})^{\mathrm {T}}({\mathbf {x} }-{\boldsymbol {\mu }}) \right) }{\sqrt {(2\pi )^{N}|{\boldsymbol{\sigma}^2}|}} \]](form_201.png)
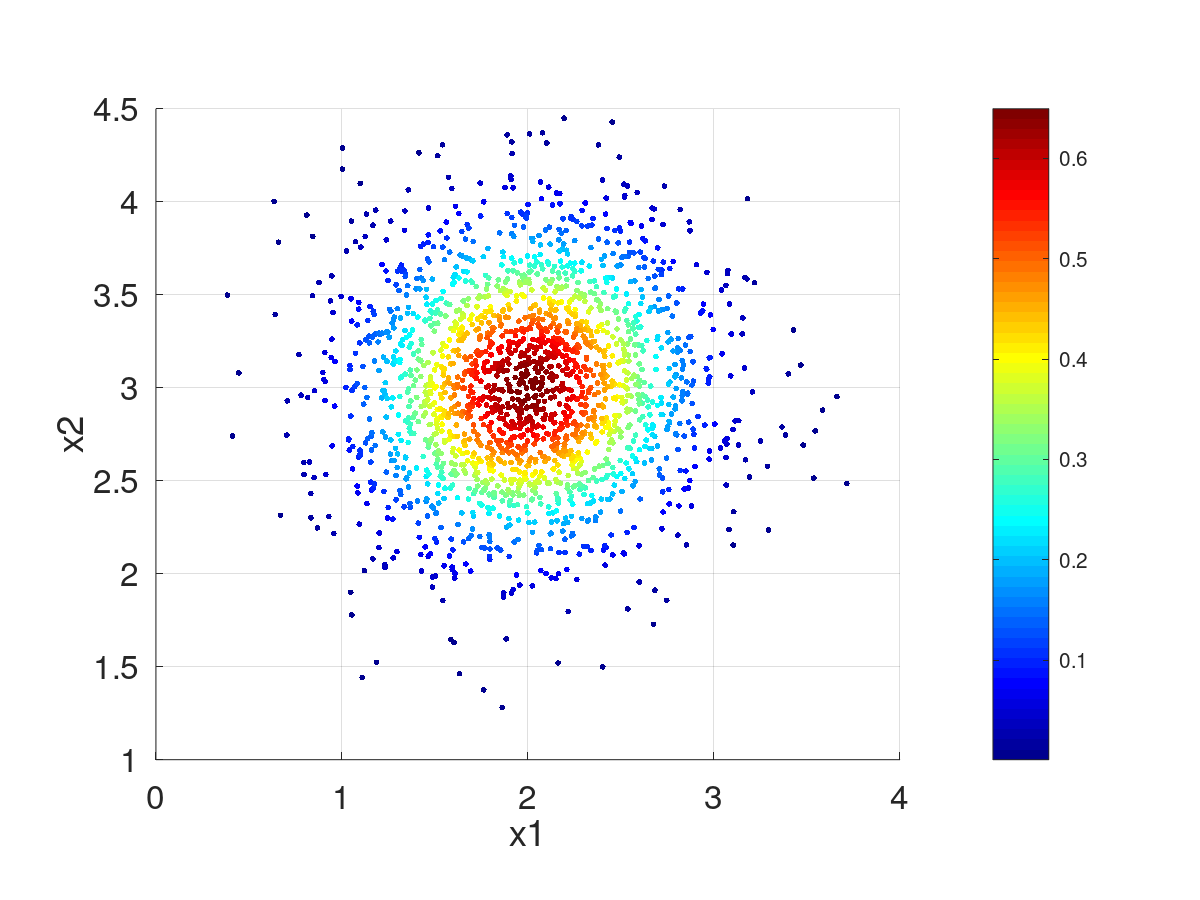
| [in] | X | Matriz con los vectores de datos (muestras de tamaño |
| [in] | Mu | Vector |
| [in] | Sigma | Desvio padrao de X. |
| Pds::Vector Pds::Probability::MGaussian | ( | const Pds::Matrix & | X, |
| const Pds::Vector & | Mu, | ||
| const Pds::Matrix & | Sinv | ||
| ) |
Evalua la "probability density function" ![]() de una funcion gaussiana multivariada, usando
de una funcion gaussiana multivariada, usando ![]() , la matriz
, la matriz ![]() y
y ![]() .
.
![\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_{0}^T\\ \mathbf{x}_{1}^T\\ \vdots\\ \mathbf{x}_{l}^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) \qquad \rightarrow \qquad \mathbf{Y}= \left( \begin{matrix} p(\mathbf{x}_{0};\mathbf{\mu},\mathbf{\Sigma})\\ p(\mathbf{x}_{1};\mathbf{\mu},\mathbf{\Sigma})\\ \vdots\\ p(\mathbf{x}_{l};\mathbf{\mu},\mathbf{\Sigma})\\ \vdots\\ p(\mathbf{x}_{L-1};\mathbf{\mu},\mathbf{\Sigma})\\ \end{matrix} \right) \]](form_206.png)
![\[ p(\mathbf{x};\mathbf{\mu},\mathbf{\Sigma})= \frac{ \exp \left( -\frac {1}{2}({\mathbf{x}}-{\boldsymbol{\mu}})^{\mathrm {T}}{\boldsymbol{\Sigma }}^{-1}({\mathbf {x} }-{\boldsymbol {\mu }}) \right) }{\sqrt {(2\pi )^{N}|{\boldsymbol {\Sigma }}|}} \]](form_207.png)
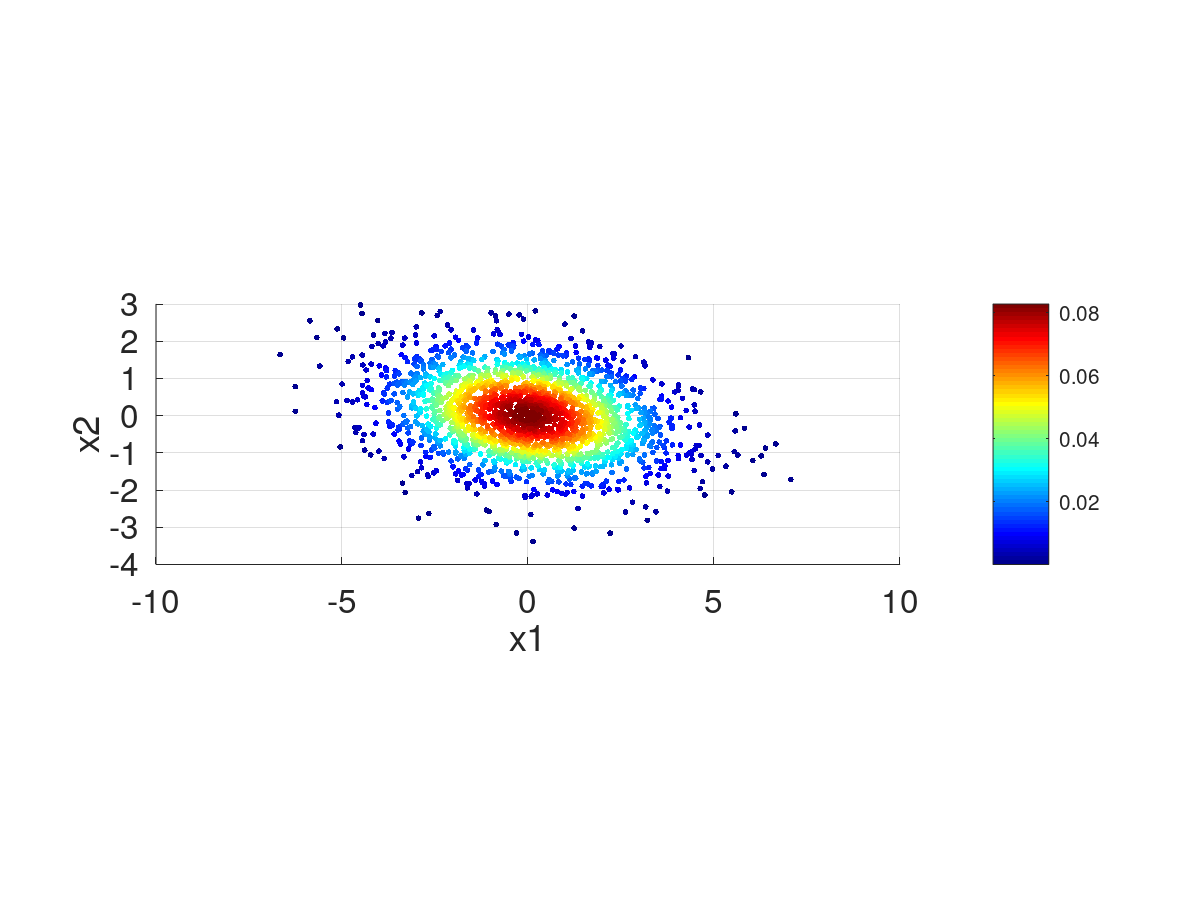
| [in] | X | Matriz con los vectores de datos (muestras de tamaño |
| [in] | Mu | Vector |
| [in] | Sinv | Matriz |
| Pds::Vector Pds::Probability::MGaussian | ( | const Pds::Matrix & | X, |
| const Pds::Vector & | Mu, | ||
| const Pds::Matrix & | Sinv, | ||
| double | det | ||
| ) |
Evalua la "probability density function" ![]() de una funcion gaussiana multivariada, usando
de una funcion gaussiana multivariada, usando ![]() , la matriz
, la matriz ![]() y
y ![]() .
.
![\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_{0}^T\\ \mathbf{x}_{1}^T\\ \vdots\\ \mathbf{x}_{l}^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) \qquad \rightarrow \qquad \mathbf{Y}= \left( \begin{matrix} p(\mathbf{x}_{0};\mathbf{\mu},\mathbf{\Sigma})\\ p(\mathbf{x}_{1};\mathbf{\mu},\mathbf{\Sigma})\\ \vdots\\ p(\mathbf{x}_{l};\mathbf{\mu},\mathbf{\Sigma})\\ \vdots\\ p(\mathbf{x}_{L-1};\mathbf{\mu},\mathbf{\Sigma})\\ \end{matrix} \right) \]](form_206.png)
![\[ p(\mathbf{x};\mathbf{\mu},\mathbf{\Sigma})= \frac{ \exp \left( -\frac {1}{2}({\mathbf{x}}-{\boldsymbol{\mu}})^{\mathrm {T}}{\boldsymbol{\Sigma }}^{-1}({\mathbf {x} }-{\boldsymbol {\mu }}) \right) }{\sqrt {(2\pi )^{N}|{\boldsymbol {\Sigma }}|}} \]](form_207.png)

| [in] | X | Matriz con los vectores de datos (muestras de tamaño |
| [in] | Mu | Vector |
| [in] | Sinv | Matriz |
| [in] | det | Determinante de |
| Pds::Vector Pds::Probability::GMMDensity | ( | const Pds::Matrix & | X, |
| const std::vector< double > & | Pi, | ||
| const std::vector< Pds::Vector > & | Mu, | ||
| const std::vector< Pds::Matrix > & | Sinv | ||
| ) |
Retorna el vector ![]() . Con este fin, evalua la "Gaussian mixture probability density function"
. Con este fin, evalua la "Gaussian mixture probability density function" ![]() usando
usando 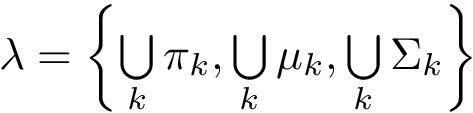 , donde
, donde ![]() .
.
![\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_{0}^T\\ \mathbf{x}_{1}^T\\ \vdots\\ \mathbf{x}_{l}^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) \qquad \rightarrow \qquad \mathbf{p}= \left( \begin{matrix} \phi(\mathbf{x}_{0};\mathbf{\lambda})\\ \phi(\mathbf{x}_{1};\mathbf{\lambda})\\ \vdots\\ \phi(\mathbf{x}_{l};\mathbf{\lambda})\\ \vdots\\ \phi(\mathbf{x}_{L-1};\mathbf{\lambda})\\ \end{matrix} \right) \]](form_219.png)
![\[ \phi(\mathbf{x};\mathbf{\lambda})=\sum\limits_{k}^{K}\pi_k~p(\mathbf{x};\mathbf{\mu}_k,\mathbf{\Sigma}_k) \]](form_220.png)
![\[ p(\mathbf{x};\mathbf{\mu}_k,\mathbf{\Sigma}_k)= \frac{ \exp \left( -\frac {1}{2}({\mathbf{x}}-{\boldsymbol{\mu_k}})^{\mathrm {T}}{\boldsymbol{\Sigma }}_k^{-1}({\mathbf {x} }-{\boldsymbol {\mu_k }}) \right) }{\sqrt {(2\pi )^{N}|{\boldsymbol {\Sigma}_k}|}} \]](form_221.png)
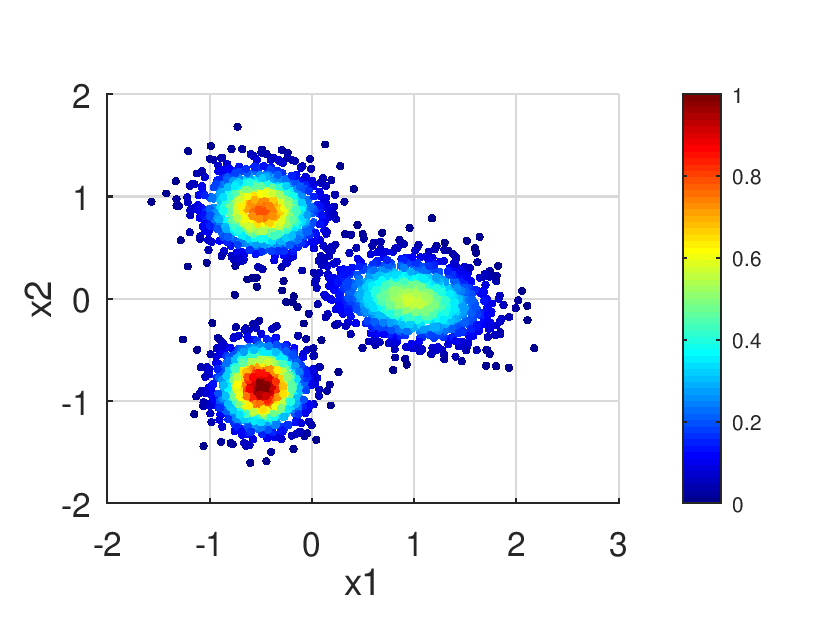
| [in] | X | Matriz con los vectores de datos (muestras de tamaño |
| [in] | Pi | Vector con mixture Weights |
| [in] | Mu | Vector con |
| [in] | Sinv | Vector con |
| Pds::Vector Pds::Probability::GMMDensity | ( | const Pds::Matrix & | X, |
| const std::vector< double > & | Pi, | ||
| const std::vector< Pds::Vector > & | Mu, | ||
| const std::vector< Pds::Matrix > & | Sinv, | ||
| const std::vector< double > & | Det | ||
| ) |
Retorna el vector ![]() . Con este fin, evalua la "Gaussian mixture probability density function"
. Con este fin, evalua la "Gaussian mixture probability density function" ![]() usando
usando 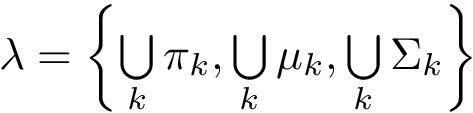 , donde
, donde ![]() .
.
![\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_{0}^T\\ \mathbf{x}_{1}^T\\ \vdots\\ \mathbf{x}_{l}^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) \qquad \rightarrow \qquad \mathbf{p}= \left( \begin{matrix} \phi(\mathbf{x}_{0};\mathbf{\lambda})\\ \phi(\mathbf{x}_{1};\mathbf{\lambda})\\ \vdots\\ \phi(\mathbf{x}_{l};\mathbf{\lambda})\\ \vdots\\ \phi(\mathbf{x}_{L-1};\mathbf{\lambda})\\ \end{matrix} \right) \]](form_219.png)
![\[ \phi(\mathbf{x};\mathbf{\lambda})=\sum\limits_{k}^{K}\pi_k~p(\mathbf{x};\mathbf{\mu}_k,\mathbf{\Sigma}_k) \]](form_220.png)
![\[ p(\mathbf{x};\mathbf{\mu}_k,\mathbf{\Sigma}_k)= \frac{ \exp \left( -\frac {1}{2}({\mathbf{x}}-{\boldsymbol{\mu_k}})^{\mathrm {T}}{\boldsymbol{\Sigma }}_k^{-1}({\mathbf {x} }-{\boldsymbol {\mu_k }}) \right) }{\sqrt {(2\pi )^{N}|{\boldsymbol {\Sigma}_k}|}} \]](form_221.png)

| [in] | X | Matriz con los vectores de datos (muestras de tamaño |
| [in] | Pi | Vector con mixture Weights |
| [in] | Mu | Vector con |
| [in] | Sinv | Vector con |
| [in] | Det | Vector con las determinantes |
| Pds::Vector Pds::Probability::GMMDensity | ( | const Pds::Matrix & | X, |
| const Pds::DataGMM & | Dat | ||
| ) |
Retorna el vector ![]() . Con este fin, evalua la "Gaussian mixture probability density function"
. Con este fin, evalua la "Gaussian mixture probability density function" ![]() usando
usando 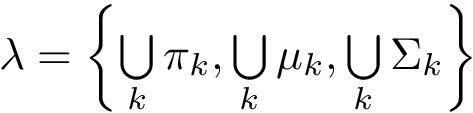 , donde
, donde ![]() .
.
![\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_{0}^T\\ \mathbf{x}_{1}^T\\ \vdots\\ \mathbf{x}_{l}^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) \qquad \rightarrow \qquad \mathbf{p}= \left( \begin{matrix} \phi(\mathbf{x}_{0};\mathbf{\lambda})\\ \phi(\mathbf{x}_{1};\mathbf{\lambda})\\ \vdots\\ \phi(\mathbf{x}_{l};\mathbf{\lambda})\\ \vdots\\ \phi(\mathbf{x}_{L-1};\mathbf{\lambda})\\ \end{matrix} \right) \]](form_219.png)
![\[ \phi(\mathbf{x};\mathbf{\lambda})=\sum\limits_{k}^{K}\pi_k~p(\mathbf{x};\mathbf{\mu}_k,\mathbf{\Sigma}_k) \]](form_220.png)
![\[ p(\mathbf{x};\mathbf{\mu}_k,\mathbf{\Sigma}_k)= \frac{ \exp \left( -\frac {1}{2}({\mathbf{x}}-{\boldsymbol{\mu_k}})^{\mathrm {T}}{\boldsymbol{\Sigma }}_k^{-1}({\mathbf {x} }-{\boldsymbol {\mu_k }}) \right) }{\sqrt {(2\pi )^{N}|{\boldsymbol {\Sigma}_k}|}} \]](form_221.png)

| [in] | X | Matriz con los vectores de datos (muestras de tamaño |
| [in] | Dat | Bloque de datos con |
| Pds::Matrix Pds::Probability::GMMPartial | ( | const Pds::Matrix & | X, |
| const std::vector< double > & | Pi, | ||
| const std::vector< Pds::Vector > & | Mu, | ||
| const std::vector< Pds::Matrix > & | Sinv | ||
| ) |
Retorna una Matriz ![]() . Con este fin, evalua la "Gaussian mixture model partial probability density function"
. Con este fin, evalua la "Gaussian mixture model partial probability density function" ![]() usando
usando ![]() .
.
![\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_{0}^T\\ \mathbf{x}_{1}^T\\ \vdots\\ \mathbf{x}_{l}^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) \qquad \rightarrow \qquad \mathbf{P}=\{\mathbf{p}_0,\mathbf{p}_1, ...,\mathbf{p}_{K-1}\} \qquad \rightarrow \qquad \mathbf{p}_k= \left( \begin{matrix} \gamma(\mathbf{x}_{0};\mathbf{\lambda}_k)\\ \gamma(\mathbf{x}_{1};\mathbf{\lambda}_k)\\ \vdots\\ \gamma(\mathbf{x}_{l};\mathbf{\lambda}_k)\\ \vdots\\ \gamma(\mathbf{x}_{L-1};\mathbf{\lambda}_k)\\ \end{matrix} \right) \]](form_231.png)
![]()
![\[ p(\mathbf{x};\mathbf{\mu}_k,\mathbf{\Sigma}_k)= \frac{ \exp \left( -\frac {1}{2}({\mathbf{x}}-{\boldsymbol{\mu_k}})^{\mathrm {T}}{\boldsymbol{\Sigma }}_k^{-1}({\mathbf {x} }-{\boldsymbol {\mu_k }}) \right) }{\sqrt {(2\pi )^{N}|{\boldsymbol {\Sigma}_k}|}} \]](form_221.png)

| [in] | X | Matriz con los vectores de datos (muestras de tamaño |
| [in] | Pi | Vector con mixture Weights |
| [in] | Mu | Vector con |
| [in] | Sinv | Vector con |
| Pds::Matrix Pds::Probability::GMMPartial | ( | const Pds::Matrix & | X, |
| const std::vector< double > & | Pi, | ||
| const std::vector< Pds::Vector > & | Mu, | ||
| const std::vector< Pds::Matrix > & | Sinv, | ||
| const std::vector< double > & | Det | ||
| ) |
Retorna una Matriz ![]() . Con este fin, evalua la "Gaussian mixture model partial probability density function"
. Con este fin, evalua la "Gaussian mixture model partial probability density function" ![]() usando
usando ![]() .
.
![\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_{0}^T\\ \mathbf{x}_{1}^T\\ \vdots\\ \mathbf{x}_{l}^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) \qquad \rightarrow \qquad \mathbf{P}=\{\mathbf{p}_0,\mathbf{p}_1, ...,\mathbf{p}_{K-1}\} \qquad \rightarrow \qquad \mathbf{p}_k= \left( \begin{matrix} \gamma(\mathbf{x}_{0};\mathbf{\lambda}_k)\\ \gamma(\mathbf{x}_{1};\mathbf{\lambda}_k)\\ \vdots\\ \gamma(\mathbf{x}_{l};\mathbf{\lambda}_k)\\ \vdots\\ \gamma(\mathbf{x}_{L-1};\mathbf{\lambda}_k)\\ \end{matrix} \right) \]](form_231.png)
![]()
![\[ p(\mathbf{x};\mathbf{\mu}_k,\mathbf{\Sigma}_k)= \frac{ \exp \left( -\frac {1}{2}({\mathbf{x}}-{\boldsymbol{\mu_k}})^{\mathrm {T}}{\boldsymbol{\Sigma }}_k^{-1}({\mathbf {x} }-{\boldsymbol {\mu_k }}) \right) }{\sqrt {(2\pi )^{N}|{\boldsymbol {\Sigma}_k}|}} \]](form_221.png)

| [in] | X | Matriz con los vectores de datos (muestras de tamaño |
| [in] | Pi | Vector con mixture Weights |
| [in] | Mu | Vector con |
| [in] | Sinv | Vector con |
| [in] | Det | Vector con |
| Pds::Matrix Pds::Probability::GMMPartial | ( | const Pds::Matrix & | X, |
| const Pds::DataGMM & | Dat | ||
| ) |
Retorna una Matriz ![]() . Con este fin, evalua la "Gaussian mixture model partial probability density function"
. Con este fin, evalua la "Gaussian mixture model partial probability density function" ![]() usando
usando ![]() .
.
![\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_{0}^T\\ \mathbf{x}_{1}^T\\ \vdots\\ \mathbf{x}_{l}^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) \qquad \rightarrow \qquad \mathbf{P}=\{\mathbf{p}_0,\mathbf{p}_1, ...,\mathbf{p}_{K-1}\} \qquad \rightarrow \qquad \mathbf{p}_k= \left( \begin{matrix} \gamma(\mathbf{x}_{0};\mathbf{\lambda}_k)\\ \gamma(\mathbf{x}_{1};\mathbf{\lambda}_k)\\ \vdots\\ \gamma(\mathbf{x}_{l};\mathbf{\lambda}_k)\\ \vdots\\ \gamma(\mathbf{x}_{L-1};\mathbf{\lambda}_k)\\ \end{matrix} \right) \]](form_231.png)
![]()
![\[ p(\mathbf{x};\mathbf{\mu}_k,\mathbf{\Sigma}_k)= \frac{ \exp \left( -\frac {1}{2}({\mathbf{x}}-{\boldsymbol{\mu_k}})^{\mathrm {T}}{\boldsymbol{\Sigma }}_k^{-1}({\mathbf {x} }-{\boldsymbol {\mu_k }}) \right) }{\sqrt {(2\pi )^{N}|{\boldsymbol {\Sigma}_k}|}} \]](form_221.png)

| [in] | X | Matriz con los vectores de datos (muestras de tamaño |
| [in] | Dat | Bloque de datos con |
| Pds::Vector Pds::Probability::PWCDensity | ( | const Pds::Matrix & | X, |
| const Pds::Matrix & | C, | ||
| const Pds::Matrix & | Sinv, | ||
| double | h = 0.1 |
||
| ) |
Retorna un vector ![]() . Con este fin, evalua la "Parzen Window Classifier probability density function"
. Con este fin, evalua la "Parzen Window Classifier probability density function" ![]() .
.
![\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_{0}^T\\ \mathbf{x}_{1}^T\\ \vdots\\ \mathbf{x}_{l}^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) \qquad \rightarrow \qquad \mathbf{p}= \left( \begin{matrix} \phi(\mathbf{x}_{0};\mathbf{C},\Sigma^{-1},h)\\ \phi(\mathbf{x}_{1};\mathbf{C},\Sigma^{-1},h)\\ \vdots\\ \phi(\mathbf{x}_{l};\mathbf{C},\Sigma^{-1},h)\\ \vdots\\ \phi(\mathbf{x}_{L-1};\mathbf{C},\Sigma^{-1},h)\\ \end{matrix} \right) \]](form_235.png)
![\[ \phi(\mathbf{x};\mathbf{C},\Sigma^{-1},h)=\frac{1}{K}{}\sum\limits_{k}^{K}p(\mathbf{x};\mathbf{c}_k,\mathbf{\Sigma}^{-1}/h^2) \]](form_236.png)
![\[ p(\mathbf{x};\mathbf{c}_k,\mathbf{\Sigma}^{-1}/h^2)= \frac{ \exp \left( -\frac {1}{2h^2}({\mathbf{x}}-{\mathbf{c}_k})^{\mathrm {T}}{\boldsymbol{\Sigma }}^{-1}({\mathbf {x} }-{\mathbf{c}_k}) \right) }{h^n\sqrt {(2\pi )^{N}|{\boldsymbol{\Sigma}}|}} \]](form_237.png)
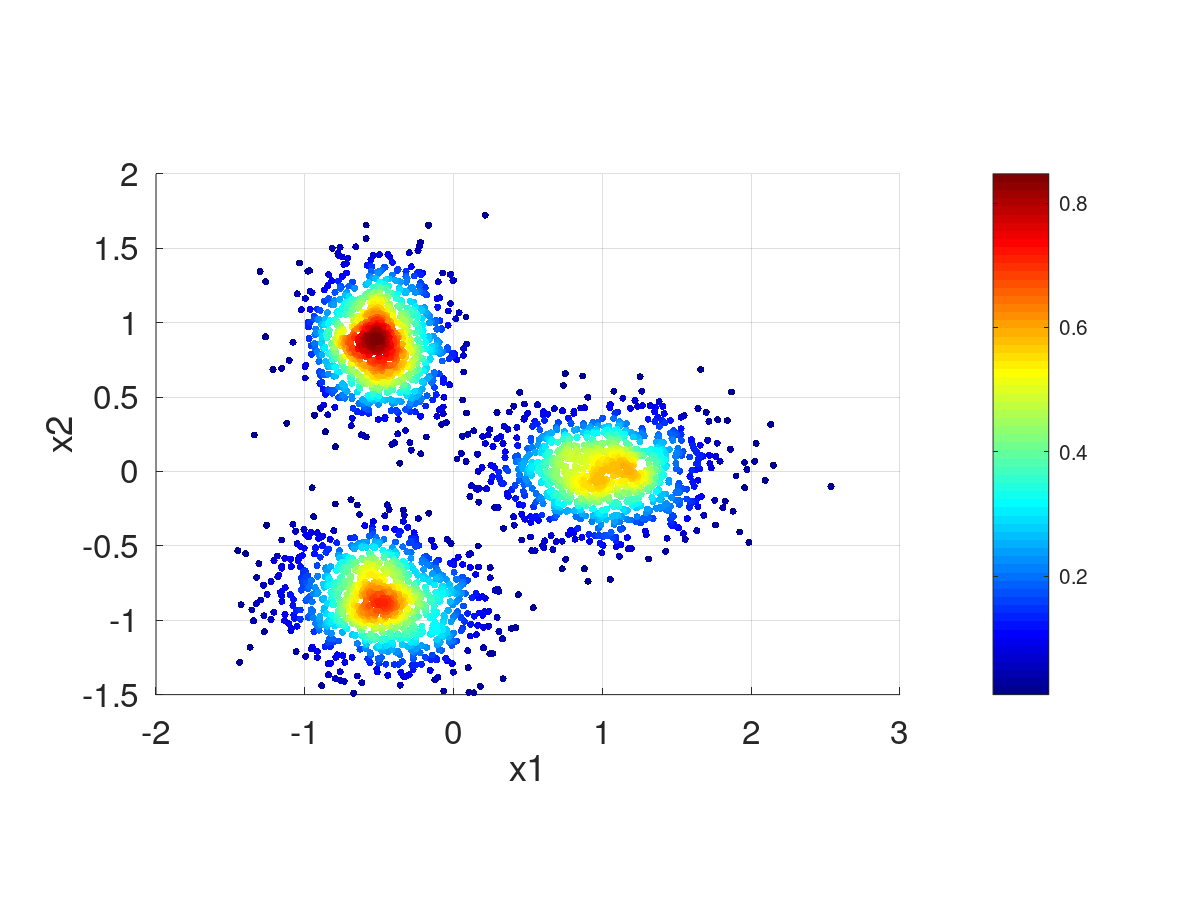
| [in] | X | Matriz de |
| [in] | C | Matriz de |
| [in] | Sinv | Matriz |
| [in] | h | Factor de suma. Es como cambiar |
| Pds::Vector Pds::Probability::PWCDensity | ( | const Pds::Matrix & | X, |
| const Pds::Matrix & | C, | ||
| const Pds::Matrix & | Sinv, | ||
| double | h, | ||
| double | det | ||
| ) |
Retorna un vector ![]() . Con este fin, evalua la "Parzen Window Classifier probability density function"
. Con este fin, evalua la "Parzen Window Classifier probability density function" ![]() .
.
![\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_{0}^T\\ \mathbf{x}_{1}^T\\ \vdots\\ \mathbf{x}_{l}^T\\ \vdots\\ \mathbf{x}_{L-1}^T\\ \end{matrix} \right) \qquad \rightarrow \qquad \mathbf{p}= \left( \begin{matrix} \phi(\mathbf{x}_{0};\mathbf{C},\Sigma^{-1},h)\\ \phi(\mathbf{x}_{1};\mathbf{C},\Sigma^{-1},h)\\ \vdots\\ \phi(\mathbf{x}_{l};\mathbf{C},\Sigma^{-1},h)\\ \vdots\\ \phi(\mathbf{x}_{L-1};\mathbf{C},\Sigma^{-1},h)\\ \end{matrix} \right) \]](form_235.png)
![\[ \phi(\mathbf{x};\mathbf{C},\Sigma^{-1},h)=\frac{1}{K}{}\sum\limits_{k}^{K}p(\mathbf{x};\mathbf{c}_k,\mathbf{\Sigma}^{-1}/h^2) \]](form_236.png)
![\[ p(\mathbf{x};\mathbf{c}_k,\mathbf{\Sigma}^{-1}/h^2)= \frac{ \exp \left( -\frac {1}{2h^2}({\mathbf{x}}-{\mathbf{c}_k})^{\mathrm {T}}{\boldsymbol{\Sigma }}^{-1}({\mathbf {x} }-{\mathbf{c}_k}) \right) }{h^n\sqrt {(2\pi )^{N}|{\boldsymbol{\Sigma}}|}} \]](form_237.png)

| [in] | X | Matriz de |
| [in] | C | Matriz de |
| [in] | Sinv | Matriz |
| [in] | h | Factor de suma. Es como cambiar |
| [in] | det | Determinante de |
 1.9.2
1.9.2