Home | Develop | Download | Contact
Namespaces
Funciones Pds::Matrix – Kernel
Matrices y vectores

Funciones que usan Pds::Matrix, Ejemplo: Pds::Gabor(), Pds::qGabor(), etc. Más...

Namespaces

namespace  Pds
 Nombre de espacio para Pds (Procesamiento Digital de Senales)
 

funciones con matrices con kernels

Descripción de algunos kernels que usan Pds::Matrix.

Pds::Matrix Pds::Kernel2D::Gaussian (unsigned int k, double Sigma=1.0)
 Retorna un filtro Gaussiano discreto.
Más...
 
double Pds::Kernel2D::GaussianSigmaFit (unsigned int rm, unsigned int r)
 Retorna o valor $\sigma$ de un filtro Gaussiano discreto.
Más...
 
Pds::Matrix Pds::Kernel2D::GaussianDiff (unsigned int k, double Sigma1=1.0, double Sigma2=1.2)
 Retorna un filtro diferencia de Gaussiano discreto.
Más...
 
Pds::Matrix Pds::Kernel2D::Gabor (unsigned int L, double Vmax=6.0, double Sigma=5.5, double Theta=Pds::Ra::Pi/4, double Lambda=4.0, double Psi=0.0)
 Retorna un kernel Gabor.
Más...
 
Pds::Matrix Pds::Kernel2D::qGabor (unsigned int L, double Vmax=6.0, double q=0.1, double Sigma=5.5, double Theta=Pds::Ra::Pi/4, double Lambda=4.0, double Psi=0)
 Retorna un kernel qGabor.
Más...
 
Pds::Matrix Pds::Kernel2D::SobelH (void)
 Retorna un kernel Sobel horizontal ([4] pp. 126).
Más...
 
Pds::Matrix Pds::Kernel2D::SobelV (void)
 Retorna un kernel Sobel vertical ([4] pp. 126).
Más...
 
Pds::Matrix Pds::Kernel2D::PrewittH (void)
 Retorna un kernel Prewitt horizontal ([4] pp. 121-122). Más...
 
Pds::Matrix Pds::Kernel2D::PrewittV (void)
 Retorna un kernel Prewitt vertical ([4] pp. 121-122).
Más...
 
Pds::Matrix Pds::Kernel2D::Laplacian5P (void)
 Retorna un operador Laplace discreto.
Más...
 
Pds::Matrix Pds::Kernel2D::Laplacian9P (void)
 Retorna un operador Laplace discreto.
Más...
 
Pds::Matrix Pds::Kernel2D::Mean (unsigned int L)
 Retorna un kernel Mean.
Más...
 

Descripción detallada

Funciones que usan Pds::Matrix, Ejemplo: Pds::Gabor(), Pds::qGabor(), etc.

#include <Pds/FuncMatrixKernel>


Estas funciones trabajan con una matriz de la forma.

\[ \mathbf{A}=\left(\begin{matrix} a_{00} & a_{01} & \cdots & a_{0(Ncol-1)}\\ a_{10} & a_{11} & \cdots & a_{1(Ncol-1)}\\ \vdots & \vdots & \vdots & \vdots \\ a_{(Nlin-2)0} & a_{(Nlin-2)1} & \cdots & a_{(Nlin-2)(Ncol-1)}\\ a_{(Nlin-1)0} & a_{(Nlin-1)1} & \cdots & a_{(Nlin-1)(Ncol-1)}\\ \end{matrix}\right) \]

\[ A\equiv [a_{i,j}] \]

nlin es el número de lineas y ncol es el número de columnas.

Informacion adicional puede ser encontrada en [5]

Documentación de las funciones

◆ Gaussian()

Pds::Matrix Pds::Kernel2D::Gaussian ( unsigned int  k,
double  Sigma = 1.0 
)

Retorna un filtro Gaussiano discreto.

\[ G_{ij}= \frac{exp{\left(-{\frac {(i-k)^{2}+(j-k)^{2}}{2\sigma ^{2}}}\right)}}{2\pi \sigma ^{2}} ; 0\leq i,j< (2k+1) \]

Pds::Kernel2D::Gaussian(3)

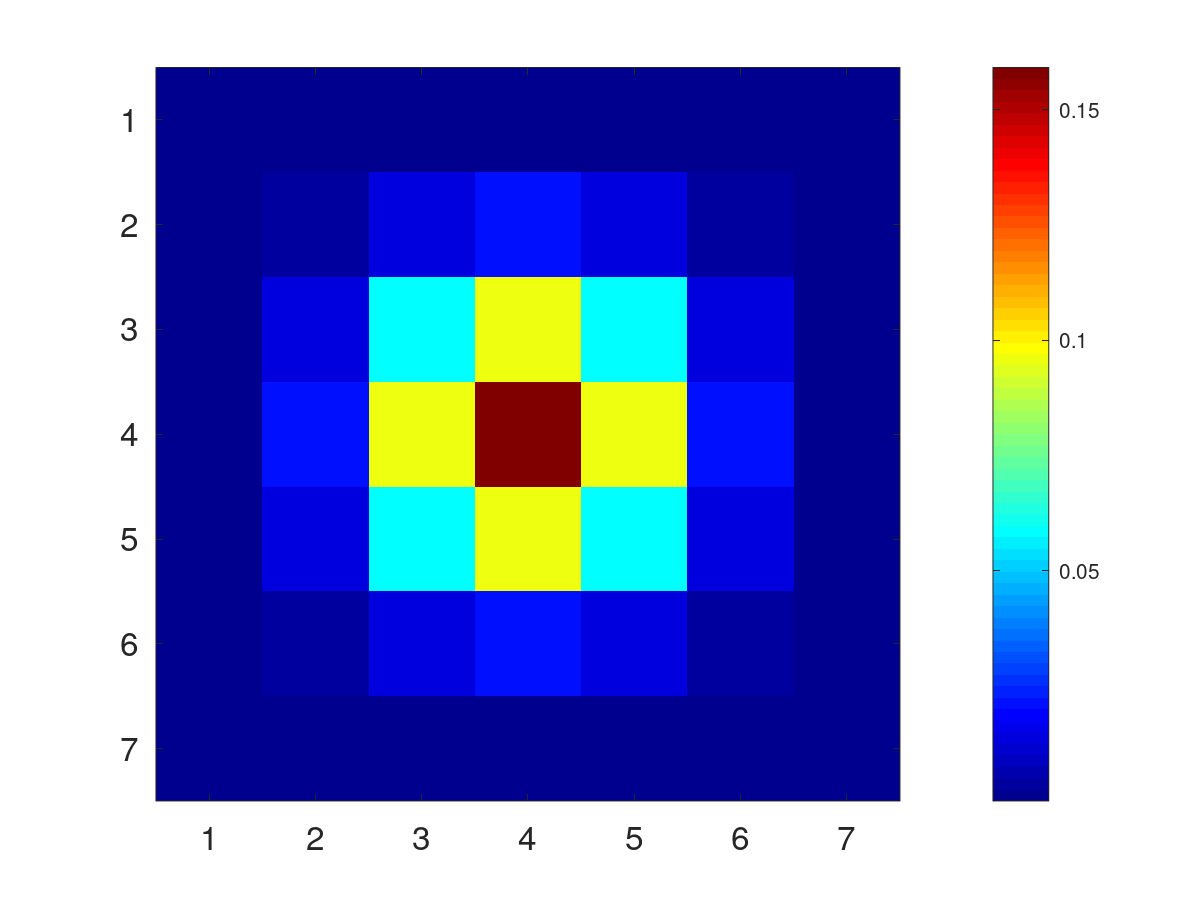
Pds::Matrix Kernel=Pds::Kernel2D::Gaussian(3);
Parámetros
[in]kValor para formar el tamaño del filtro $L=2 k+1$.
[in]Sigmaparámetro del filtro gaussiano.
Devuelve
Retorna un filtro bluer (gaussiano) en 2D.
Ejemplos
example_matrix_kernel_gaussian.cpp.

◆ GaussianSigmaFit()

double Pds::Kernel2D::GaussianSigmaFit ( unsigned int  rm,
unsigned int  r 
)

Retorna o valor $\sigma$ de un filtro Gaussiano discreto.

\[ \mathbf{G}= \begin{bmatrix} g(-r,-r) & \dots & g(-1,-r) & g(0,-r) & g(1,-r)& \dots & g(r,-r) \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ g(-r,-1) & \dots & g(-1,-1) & g(0,-1) & g(1,-1) & \dots & g(r,-1) \\ g(-r,0) & \dots & g(-1,0) & g(0,0) & g(1,0) & \dots & g(r,0) \\ g(-r,1) & \dots & g(-1,1) & g(0,1) & g(1,1) & \dots & g(r,1) \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ g(-r,r) & \dots & g(-1,r) & g(0,r) & g(1,r) & \dots & g(r,r) \\ \end{bmatrix} \]

\[ g(i,j)= \frac{exp{\left(-{\frac {i^{2}+j^{2}}{2\sigma ^{2}}}\right)}}{2\pi \sigma ^{2}} ; -r\leq i,j\leq r \]

De modo que $(\mathbf{G}-mean\left\{\mathbf{G}\right\})>0$ tiene radio $r_m$.

rm=6, r=10 --> sigma=3

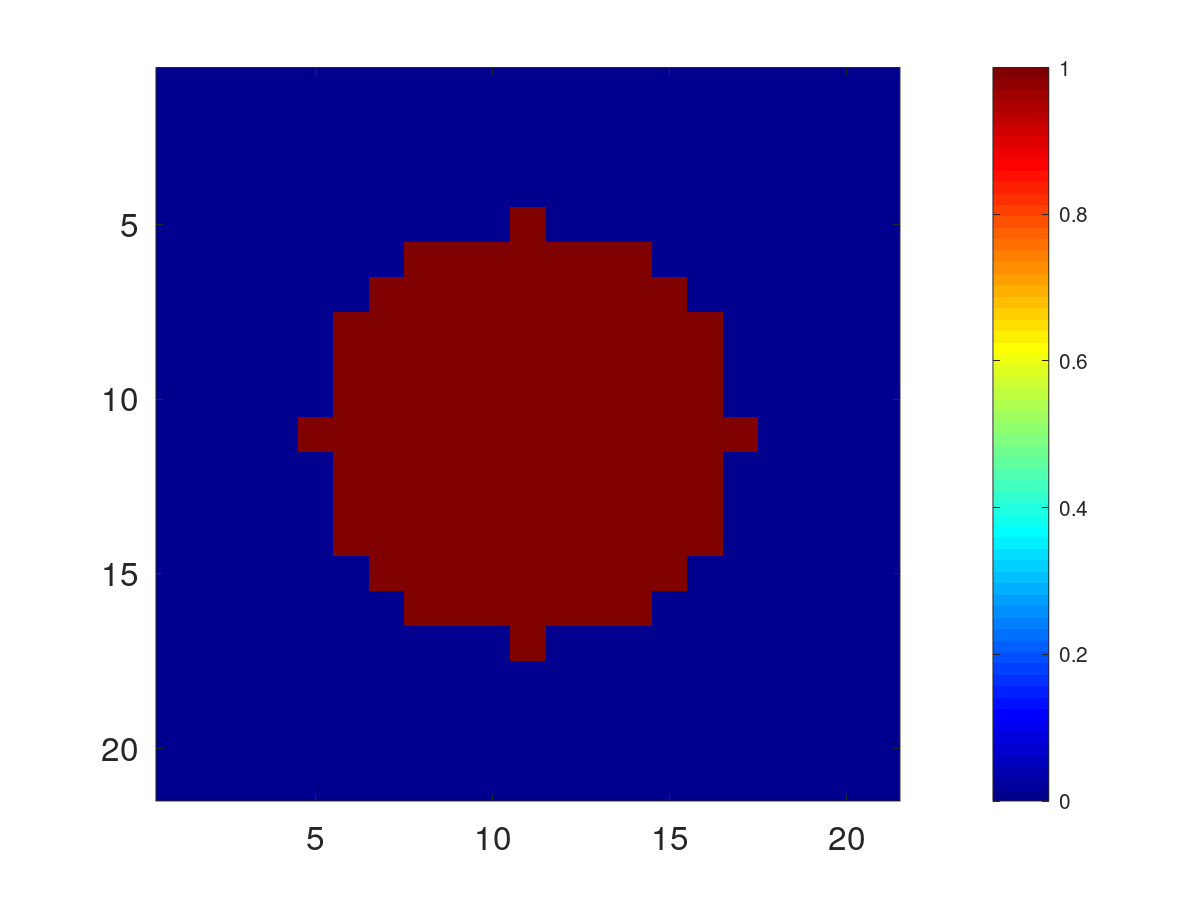
Pds::Matrix Kernel=Pds::Kernel2D::GaussianSigmaFit(6,10);
Parámetros
[in]rmValor del radio $r_m$. Obligatoriamente $r_m<r$.
[in]rValor para formar el tamaño del filtro $L=2 r+1$.
Devuelve
Retorna o valor $\sigma$.
Ejemplos
example_matrix_kernel_gaussian.cpp.

◆ GaussianDiff()

Pds::Matrix Pds::Kernel2D::GaussianDiff ( unsigned int  k,
double  Sigma1 = 1.0,
double  Sigma2 = 1.2 
)

Retorna un filtro diferencia de Gaussiano discreto.

\[ G_{ij}= \frac{exp{\left(-{\frac {(i-k)^{2}+(j-k)^{2}}{2\sigma_1^{2}}}\right)}}{2\pi \sigma_1^{2}} - \frac{exp{\left(-{\frac {(i-k)^{2}+(j-k)^{2}}{2\sigma_2^{2}}}\right)}}{2\pi \sigma_2^{2}} ; 0\leq i,j< (2k+1) \]

Pds::Kernel2D::GaussianDiff(3)

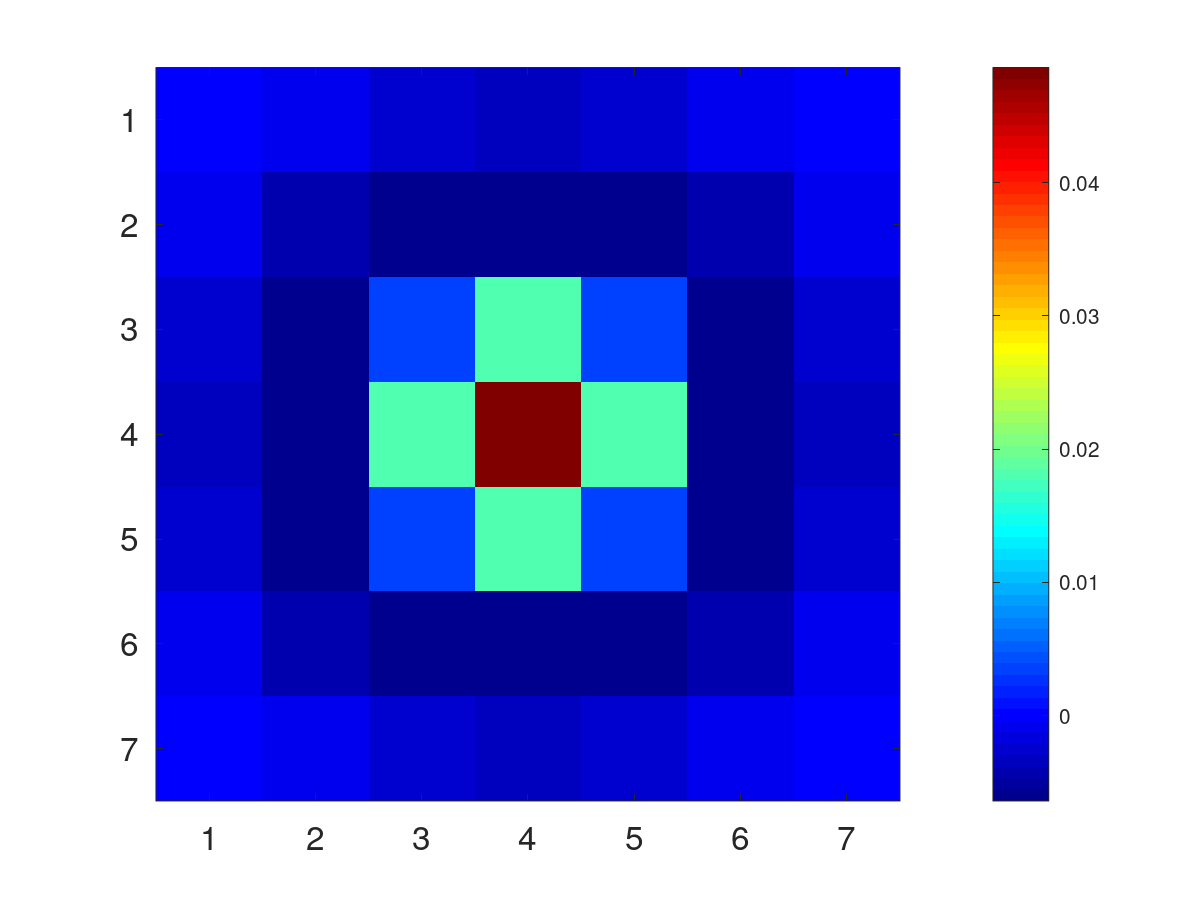
Pds::Matrix Kernel=Pds::Kernel2D::GaussianDiff(3);
Parámetros
[in]kValor para formar el tamaño del filtro $L=2 k+1$.
[in]Sigma1parámetro del filtro gaussiano.
[in]Sigma2parámetro del filtro gaussiano.
Devuelve
Retorna un diferencia de Gaussiano discreto.
Ejemplos
example_matrix_kernel_gaussian.cpp.

◆ Gabor()

Pds::Matrix Pds::Kernel2D::Gabor ( unsigned int  L,
double  Vmax = 6.0,
double  Sigma = 5.5,
double  Theta = Pds::Ra::Pi/4,
double  Lambda = 4.0,
double  Psi = 0.0 
)

Retorna un kernel Gabor.

\[ \mathbf{A}\equiv [a(i,j)] \]

\[ -Vmax\leq x\leq Vmax,\qquad -Vmax\leq y\leq Vmax \]

\[ x'=x\cos \theta +y\sin \theta, \qquad y'=-x\sin \theta +y\cos \theta \]

\[ Gabor(x,y;\lambda,\theta,\psi,\sigma) = \exp\left(-\frac{x'^2+y'^2}{2\sigma^2}\right)\cos\left(2\pi\frac{x'}{\lambda}+\psi\right) \]

Pds::Kernel2D::Gabor(49)

Pds::Matrix Kernel=Pds::Kernel2D::Gabor(49);
Parámetros
[in]LEl numero de lineas ou colunas de la matriz.
[in]VmaxValor máximo de x e y.
[in]SigmaDesvio $\sigma$ de la gausiana.
[in]ThetaAngulo $\theta$ de giro en 2D.
[in]LambdaValor $\lambda$ inverso de la frecuencia de cosenoide.
[in]PsiDesfasaje $\psi$ de la cosenoide.
Devuelve
Retorna la matriz o una matriz vacía en caso de error.
Ejemplos
example_matrix_kernel_gabor.cpp.

◆ qGabor()

Pds::Matrix Pds::Kernel2D::qGabor ( unsigned int  L,
double  Vmax = 6.0,
double  q = 0.1,
double  Sigma = 5.5,
double  Theta = Pds::Ra::Pi/4,
double  Lambda = 4.0,
double  Psi = 0 
)

Retorna un kernel qGabor.

\[ \mathbf{A}\equiv [a(i,j)] \]

\[ -Vmax\leq x\leq Vmax,\qquad -Vmax\leq y\leq Vmax \]

\[ x'=x\cos \theta +y\sin \theta, \qquad y'=-x\sin \theta +y\cos \theta \]

\[ Gabor(x,y;q,\lambda,\theta,\psi,\sigma) = exp_q\left(-\frac{x'^2+y'^2}{2\sigma^2}\right)\cos\left(2\pi\frac{x'}{\lambda}+\psi\right) \]

Pds::Kernel2D::qGabor(49)

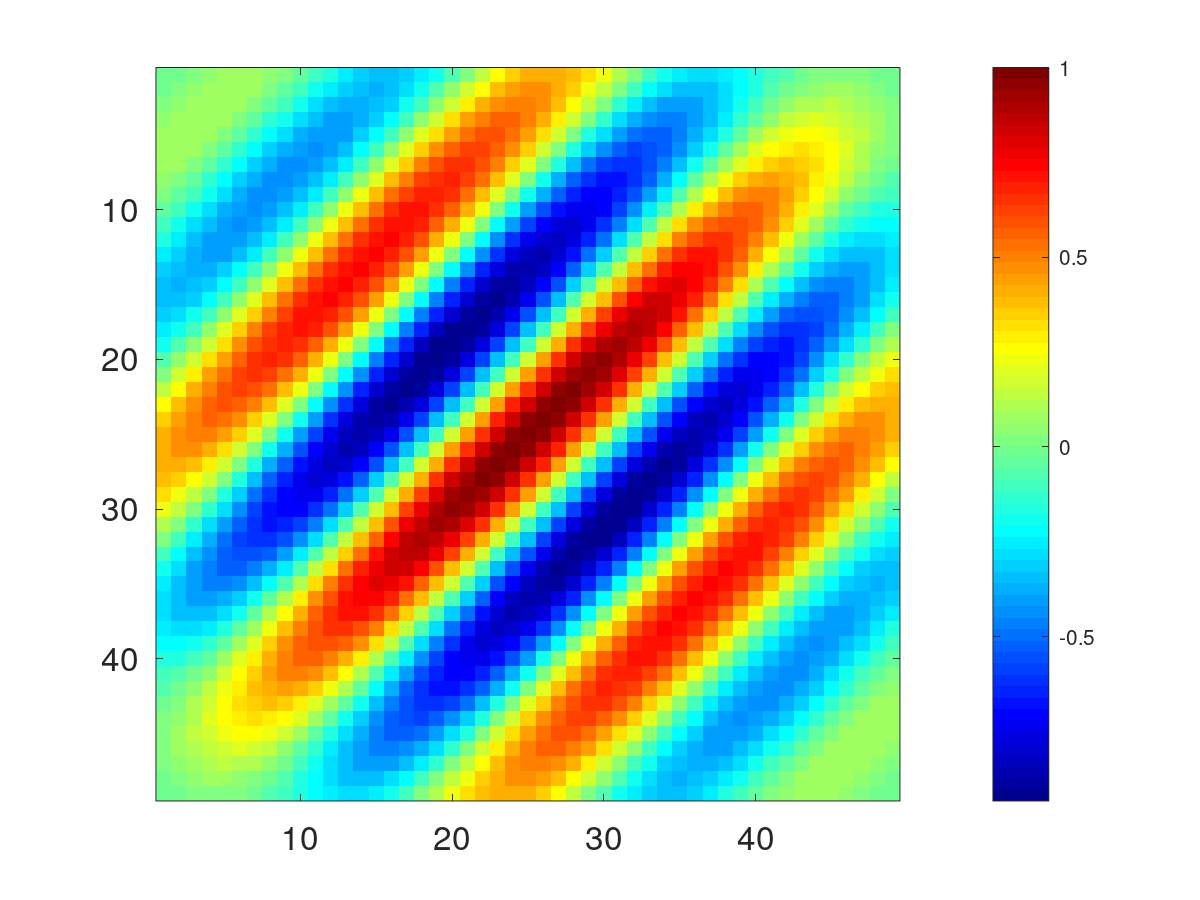
Pds::Matrix Kernel=Pds::Kernel2D::qGabor(49);
Parámetros
[in]LEl numero de lineas ou colunas de la matriz.
[in]VmaxValor máximo de x e y.
[in]qParámetro tsallis de la q-exponential, Pds::qExp().
[in]SigmaDesvio $\sigma$ de la gausiana.
[in]ThetaAngulo $\theta$ de giro en 2D.
[in]LambdaValor $\lambda$ inverso de la frecuencia de cosenoide.
[in]PsiDesfasaje $\psi$ de la cosenoide.
Devuelve
Retorna la matriz o una matriz vacía en caso de error.
Ejemplos
example_matrix_kernel_gabor.cpp.

◆ SobelH()

Pds::Matrix Pds::Kernel2D::SobelH ( void  )

Retorna un kernel Sobel horizontal ([4] pp. 126).

\[S_h\equiv \left[ \begin{matrix} -1 & -2 & -1\\ 0 & 0 & 0\\ 1 & 2 & 1\\ \end{matrix} \right] \] 


Pds::Matrix Kernel=Pds::Kernel2D::SobelH();
Devuelve
Retorna la matriz con un filtro Sobel horizontal.

◆ SobelV()

Pds::Matrix Pds::Kernel2D::SobelV ( void  )

Retorna un kernel Sobel vertical ([4] pp. 126).

\[S_h\equiv \left[ \begin{matrix} -1 & 0 & 1\\ -2 & 0 & 2\\ -1 & 0 & 1\\ \end{matrix} \right] \] 


Pds::Matrix Kernel=Pds::Kernel2D::SobelV();
Devuelve
Retorna la matriz con un filtro Sobel vertical.

◆ PrewittH()

Pds::Matrix Pds::Kernel2D::PrewittH ( void  )

Retorna un kernel Prewitt horizontal ([4] pp. 121-122).

\[P_h\equiv \left[ \begin{matrix} 1 & 1 & 1\\ 0 & 0 & 0\\ -1 & -1 & -1\\ \end{matrix} \right] \] 


Pds::Matrix Kernel=Pds::Kernel2D::PrewittH();
Devuelve
Retorna la matriz con un filtro Prewitt horizontal.

◆ PrewittV()

Pds::Matrix Pds::Kernel2D::PrewittV ( void  )

Retorna un kernel Prewitt vertical ([4] pp. 121-122).

\[P_h\equiv \left[ \begin{matrix} 1 & 0 & -1\\ 1 & 0 & -1\\ 1 & 0 & -1\\ \end{matrix} \right] \] 


Pds::Matrix Kernel=Pds::Kernel2D::PrewittV();
Devuelve
Retorna la matriz con un filtro Prewitt vertical.

◆ Laplacian5P()

Pds::Matrix Pds::Kernel2D::Laplacian5P ( void  )

Retorna un operador Laplace discreto.

Las aproximaciones del Laplaciano, obtenidas por el método de diferencias finitas o por el método de elementos finitos, también pueden llamarse Laplacianos discretos. El laplaciano en dos dimensiones se puede aproximar utilizando el five-point stencil finite-difference method ([3] pp. 61), lo que resulta en

\[ \frac{\partial^2f(x,y)}{\partial x^2} + \frac{\partial^2f(x,y)}{\partial y^2} \equiv \Delta f(x,y) \]

\[ \Delta f(x,y)\approx \frac {f(x-h,y)+f(x+h,y)+f(x,y-h)+f(x,y+h)-4f(x,y)}{h^{2}}, \]

\[\Delta \equiv L_5 = \left[ \begin{matrix} 0 & 1 & 0\\ 1 & -4 & 1\\ 0 & 1 & 0\\ \end{matrix} \right] \] 


Pds::Matrix Kernel=Pds::Kernel2D::Laplacian5P();
Devuelve
Retorna un operador Laplace discreto en 2D.

◆ Laplacian9P()

Pds::Matrix Pds::Kernel2D::Laplacian9P ( void  )

Retorna un operador Laplace discreto.

Las aproximaciones del Laplaciano, obtenidas por el método de diferencias finitas o por el método de elementos finitos, también pueden llamarse Laplacianos discretos. El laplaciano en dos dimensiones se puede aproximar utilizando el nine-point stencil finite-difference method ([3] pp. 64), lo que resulta en

\[ \frac{\partial^2f(x,y)}{\partial x^2} + \frac{\partial^2f(x,y)}{\partial y^2} \equiv \Delta f(x,y) \]

\[ \begin{array}{lll} \Delta f(x,y) &\approx& \frac {4f(x-h,y)+4f(x+h,y)+4f(x,y-h)+4f(x,y+h)}{6 h^{2}}\\ \\ ~ &~&+\frac {f(x-h,y-h)+f(x+h,y-h)+ f(x-h,y+h)+f(x+h,y+h)}{6 h^{2}}\\ \\ ~ &~&-\frac {20f(x,y)}{6 h^{2}}\\ \end{array} \]

\[\Delta \equiv L_9 = \frac{1}{6} \left[ \begin{matrix} 1 & 4 & 1\\ 4 & -20 & 4\\ 1 & 4 & 1\\ \end{matrix} \right] \] 


Pds::Matrix Kernel=Pds::Kernel2D::Laplacian9P();
Devuelve
Retorna un operador Laplace discreto en 2D.

◆ Mean()

Pds::Matrix Pds::Kernel2D::Mean ( unsigned int  L)

Retorna un kernel Mean.

\[Mean\equiv \frac{1}{L^2} \left[ \begin{matrix} 1 & 1 & ... & 1\\ 1 & 1 & ... & 1\\ \vdots & \vdots & ... & \vdots\\ 1 & 1 & ... & 1\\ \end{matrix} \right] \] 


Pds::Matrix Kernel=Pds::Kernel2D::Mean(5);
Devuelve
Retorna la matriz con un filtro Mean.

Enlaces de interés

HomePage Bazaar Download Bug report Ayuda Developer Feed
Manual de referencia generado el Martes, 10 de Octubre de 2023 18:23:42 para la biblioteca libpdsramm usando  Generado el Martes, 10 de Octubre de 2023 18:23:42 para libpdsramm por   doxygen 1.9.4