Home | Develop | Download | Contact
Funciones
Referencia del Namespace Pds::LogisticModel
Clasificadores » Clasificadores – Funciones » Funciones en el namespace Pds::LogisticModel

Nombre de espacio para LogisticModel (Logistic regression) Más...

Funciones

Pds::Vector FittingGradientIGSoft (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &W0)
 
Pds::Vector GradientCostInformationGainSoft (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y, double h)
 
Pds::Vector GradientCostInformationGainSoft2 (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y)
 
double CostInformationGainSoft (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y)
 
double CostXqEntropy (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y, double q)
 
Pds::Vector GradientCostXqEntropy (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y, double q, double h)
 
Pds::Vector GradientCostXqEntropySoft (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y, double q)
 
Logistic regression : Clasificador
Pds::Vector Classify (const Pds::Vector &W, const Pds::Matrix &X)
 Calculo del resultado del clasificador. Más...
 
Logistic regression : Función de costo
double CostInformationGain (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y)
 Calculo de costo. Más...
 
Pds::Vector GradientCostInformationGain (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y, double h)
 Calculo de costo. Más...
 
double CostCrossEntropy (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y)
 Calculo de pesos. Más...
 
double CostMeanSquare (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y)
 Calculo de pesos. Más...
 
Logistic regression : Peso inicial
Pds::Vector GetW0MeanMethod (const Pds::Matrix &X)
 Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica. Más...
 
Pds::Vector GetW0CornerMeanMethod (const Pds::Matrix &X, double Delta=0.001)
 Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica. Más...
 
Pds::Vector GetW0MeanSquareMethod (const Pds::Matrix &X)
 Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica. Más...
 
Logistic regression : Regresión de pesos : Familia Mean Square
Pds::Vector FittingLogitMeanSquare (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, double Delta=0.0001)
 Calculo de pesos. Más...
 
Pds::Vector FittingLogitMeanSquare (const Pds::Matrix &X, const Pds::Vector &Y, double Delta=0.0001)
 Calculo de pesos. Más...
 
Pds::Vector FittingLogitWeightedMeanSquare (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &D, double Delta=0.0001)
 Calculo de pesos. Más...
 
Pds::Vector FittingLogitWeightedMeanSquare (const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &D, double Delta=0.0001)
 Calculo de pesos. Más...
 
Logistic regression : Regresión de pesos : Familia Robust Mean Square
Pds::Vector FittingRobustLogitMeanSquare (const Pds::Matrix &X, const Pds::Vector &Y, double Delta=0.0001, unsigned int N=2, double Offset=0.1)
 Calculo de pesos. Más...
 
Pds::Vector FittingRobustLogitMeanSquare (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, double Delta=0.0001, unsigned int N=2, double Offset=0.1)
 Calculo de pesos. Más...
 
Logistic regression : Regresión de pesos : Familia kmeans + Information sum
Pds::Vector FittingKmeansLogitMeanSquare (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, double Delta)
 
Logistic regression : Regresión de pesos : Familia Cross Entropy
Pds::Vector FittingGradientCrossEntropy (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &W0)
 Gradiente descendente para sigmoide. Más...
 
Pds::Vector FittingGradientSVM (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &W0)
 Gradiente descendente para sigmoide. Más...
 
Logistic regression : Regresión de pesos : Familia Information Gain
Pds::Vector FittingOrtogonalIG (const Pds::Matrix &X, const Pds::Vector &Y, unsigned int MinID)
 Calculo de pesos. Más...
 
Pds::Vector FittingGradientIG (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &W0)
 Calculo de pesos. Más...
 
Pds::Vector FittingParrallelPlaneIS (const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &W0, double *ISmin=NULL, double Delta=0.001)
 Calculo de pesos buscando el plano paralelo a W0 que genere la menor suma de informaciones en la particion, es equivalente a buscar la mayor information gain. Más...
 
Logistic regression : Funciones de ajuste
Pds::Vector FittingByFactor (const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &W0, double Delta=0.001)
 Aplica la teoria de Logit MeanSquare para ajustar W0 por um factor real adecuado. Más...
 
Logistic regression : Funciones de diagnóstico
Pds::DataErrorCurve LearningCurves (Pds::IterationConf &Conf, const Pds::Matrix &Xtr, const Pds::Vector &Ytr, const Pds::Matrix &Xcv, const Pds::Vector &Ycv, double percent)
 Retorna learning curve. Más...
 

Descripción detallada

Nombre de espacio para LogisticModel (Logistic regression)

Documentación de las funciones

◆ FittingKmeansLogitMeanSquare()

Pds::Vector Pds::LogisticModel::FittingKmeansLogitMeanSquare ( Pds::IterationConf &  Conf,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
double  Delta 
)
Ejemplos
example_logisticregression_kmeanstest.cpp.

◆ FittingGradientIGSoft()

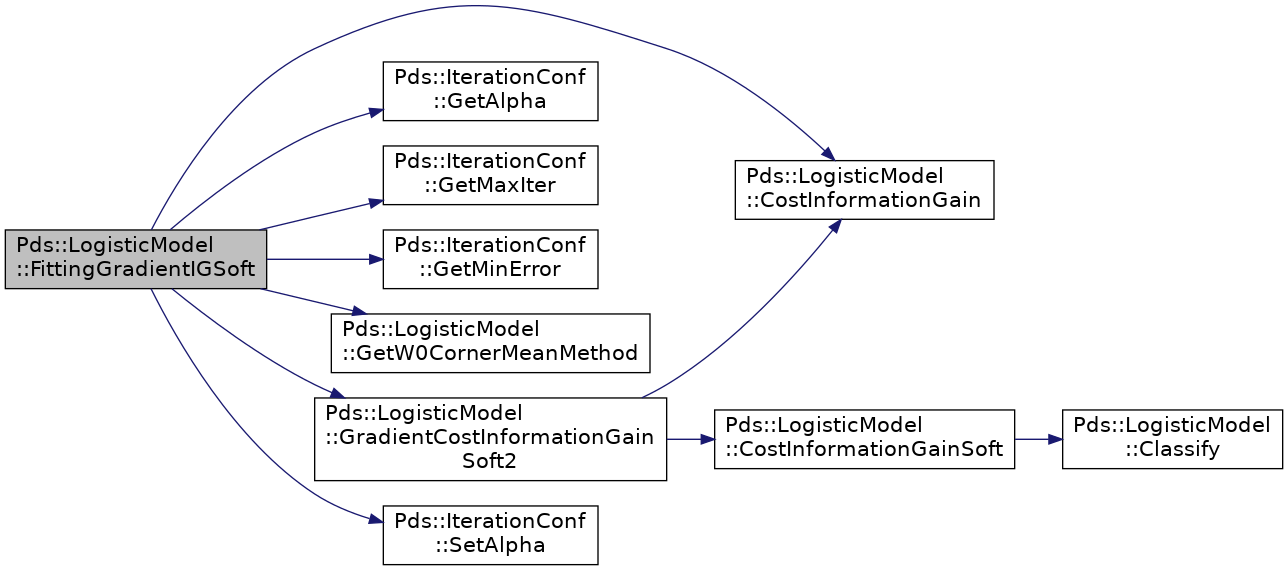
Pds::Vector Pds::LogisticModel::FittingGradientIGSoft ( Pds::IterationConf &  Conf,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
const Pds::Vector &  W0 
)

Definición en la línea 254 del archivo test_working_FittingGradientIGSoft.cpp.

258 {
259  if(W0.IsEmpty()) return Pds::Matrix();
260  if(X.IsEmpty()) return Pds::Matrix();
261  if(Y.IsEmpty()) return Pds::Matrix();
262 
263  if(X.Nlin()!=Y.Nlin()) return Pds::Matrix();
264  if(X.Ncol()!=(W0.Nlin()-1)) return Pds::Matrix();
265 
266  unsigned int YSUM=Y.Geq(0.5).Sum();
267  if(YSUM==Y.Nel()) return Pds::LogisticModel::GetW0CornerMeanMethod(X);
268  if(YSUM==0) return -Pds::LogisticModel::GetW0CornerMeanMethod(X);
269 
270  double Alpha=Conf.GetAlpha();
271  //double Gamma=Conf.GetGamma();
272  //double Lambda=Conf.GetLambda();
273  double MinError=Conf.GetMinError();
274  double MaxIter=Conf.GetMaxIter();
275 
276  pds_print_error_message("Esta función aun no trabaja bien, es demasiado abrupta");
277 
278  if(Conf.Show) print_IterationConf_IG_soft_init_data(Conf,"Gradient IG");
279 
280  Pds::Vector W=W0;
281  Pds::Vector Wopt=W;
282  Pds::Vector DIG,DCE;
283  double Costmax=-1;
284  double Cost;
285 
286 
287  Pds::Fir FIR5(Pds::Vector(5,1.0)/5);
288  //double fir5;
289  //Pds::Fir FIR10(Pds::Vector(10,1.0)/10);
290  //double fir10;
291 
292  double last_error=1000, before_error=0,delta_error=1;;
293  unsigned int iter=0;
294 
295  Pds::Matrix R=Pds::RegressorMatrix(X);
296  Pds::Vector DY,DW;
297  Pds::Matrix I=Pds::Eye(W.Nel());I.SetRaw(0,0,0);
298  Pds::Vector Yt;
299 
300 
301  std::vector<double> ig;
302  std::vector<double> err;
303 
304  double A=W.Norm()*0.1+0.01;
305 
306  do{
307  //double h;
308  //h=W.RMS()*0.5;
309  //DIG=Pds::LogisticModel::GradientCostInformationGainSoft(W,X,Y,h);
310  DW=-Pds::LogisticModel::GradientCostInformationGainSoft2(W,X,Y);
311  DW.T().Print("DW: ");
312  DW=(A/DW.Norm())*DW;
313  DW.T().Print("DW: ");
314 
315  W=W-Alpha*DW;
316 
317  W.T().Print(" W: ");
318 
319  Pds::Octave::Plot::PointsX2DY(X,Pds::Sigmoid(R*W),"testando.m","test_"+std::to_string(iter)+".png");
320 
321  Cost=Pds::LogisticModel::CostInformationGain(W,X,Y);
322 
323  before_error=last_error;
324 
325  last_error = 1.0-Cost;
326  //last_error += (Lambda*0.5/W.Nel())*(W.Dot(W)-W[0]*W[0]);
327 
328  delta_error=fabs(FIR5.Evaluate(last_error)-before_error);
329 
330  if(Cost>Costmax)
331  {
332  Costmax=Cost;
333  Wopt=W;
334  }
335 
336  ig.push_back(Cost);
337  err.push_back(last_error);
338 
339  iter++;
340 
341  //if(Conf.Show) print_iterative_IG_soft_data(iter,Alpha,delta_error,Cost,true);
342 
343  }while( (delta_error>MinError)&&(iter<MaxIter) );
344 
345  if(Conf.Show) print_iterative_IG_soft_data(iter,Alpha,delta_error,Cost,true);
346 
347  Conf.SetAlpha(Alpha);
348  Conf.LastError=delta_error;
349  Conf.LastIter=iter;
350 
351  Pds::Ra::SaveStdVector(ig,"ig.txt");
352  Pds::Ra::SaveStdVector(err,"err.txt");
353 
354  if(Conf.Show) print_IterationConf_IG_soft_end_data(Conf,"Gradient IG");
355 
356  double alpha=1.0;
357  /*
358  double s2;
359  Yt=R*Wopt;
360  double Delta=0.001;
361  Pds::Matrix Yo=Y.Geq(0.5)*(1.0-2*Delta)+Delta;
362  s2=Yt.SumSquare();
363  if(s2>0) alpha=Yt.Dot(Pds::Logit(Yo))/s2;
364  else alpha=1;
365  */
366  return Wopt*alpha;
367 }
Pds::IterationConf::SetAlpha
bool SetAlpha(double Alpha)
Coloca el valor alpha.
Pds::IterationConf::GetMinError
double GetMinError(void) const
Devuelve el valor MinError.
Pds::IterationConf::GetAlpha
double GetAlpha(void) const
Devuelve el valor alpha.
Pds::IterationConf::GetMaxIter
unsigned int GetMaxIter(void) const
Devuelve el valor MaxIter.
Pds::LogisticModel::GetW0CornerMeanMethod
Pds::Vector GetW0CornerMeanMethod(const Pds::Matrix &X, double Delta=0.001)
Obtiene de forma rapida un vector inicial para usar en regresion logistica.
Pds::LogisticModel::CostInformationGain
double CostInformationGain(const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y)
Calculo de costo.
Pds::LogisticModel::GradientCostInformationGainSoft2
Pds::Vector GradientCostInformationGainSoft2(const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y)
Definition: test_working_FittingGradientIGSoft.cpp:141

Hace referencia a CostInformationGain(), Pds::IterationConf::GetAlpha(), Pds::IterationConf::GetMaxIter(), Pds::IterationConf::GetMinError(), GetW0CornerMeanMethod(), GradientCostInformationGainSoft2(), Pds::IterationConf::LastError, Pds::IterationConf::LastIter, Pds::IterationConf::SetAlpha() y Pds::IterationConf::Show.

Gráfico de llamadas para esta función:

◆ GradientCostInformationGainSoft()

Pds::Vector Pds::LogisticModel::GradientCostInformationGainSoft ( const Pds::Vector &  W,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
double  h 
)

Definición en la línea 101 del archivo test_working_FittingGradientIGSoft.cpp.

105 {
106  if(W.IsEmpty()) return Pds::Vector();
107  if(X.IsEmpty()) return Pds::Vector();
108  if(Y.IsEmpty()) return Pds::Vector();
109 
110  if(X.Nlin()!=Y.Nlin()) return Pds::Vector();
111  if(X.Ncol()!=(W.Nlin()-1)) return Pds::Vector();
112 
113  if(h==0.0) return Pds::Vector();
114 
115  unsigned int N=W.Nel();
116 
117  Pds::Vector D(N);
118  Pds::Vector Whp(N);
119  Pds::Vector Whm(N);
120  double dn;
121 
122  Whp.Copy(W);
123  Whm.Copy(W);
124 
125  for(unsigned int n=0;n<N;n++)
126  {
127  Whp.SetRaw(n,W.GetRaw(n)+h);
128  Whm.SetRaw(n,W.GetRaw(n)-h);
129 
130  dn=( Pds::LogisticModel::CostInformationGainSoft(Whp,X,Y)
131  -Pds::LogisticModel::CostInformationGainSoft(Whm,X,Y) )/(2*h);
132 
133  D.SetRaw(n,dn);
134 
135  Whp.SetRaw(n,W.GetRaw(n));
136  Whm.SetRaw(n,W.GetRaw(n));
137  }
138  return D;
139 }
Pds::LogisticModel::CostInformationGainSoft
double CostInformationGainSoft(const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y)
Definition: test_working_FittingGradientIGSoft.cpp:51

Hace referencia a CostInformationGainSoft().

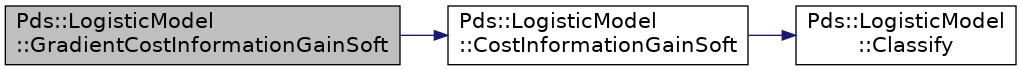
Gráfico de llamadas para esta función:

◆ GradientCostInformationGainSoft2()

Pds::Vector Pds::LogisticModel::GradientCostInformationGainSoft2 ( const Pds::Vector &  W,
const Pds::Matrix &  X,
const Pds::Vector &  Y 
)

Definición en la línea 141 del archivo test_working_FittingGradientIGSoft.cpp.

144 {
145  if(W.IsEmpty()) return Pds::Vector();
146  if(X.IsEmpty()) return Pds::Vector();
147  if(Y.IsEmpty()) return Pds::Vector();
148 
149  if(X.Nlin()!=Y.Nlin()) return Pds::Vector();
150  if(X.Ncol()!=(W.Nlin()-1)) return Pds::Vector();
151 
152  Pds::Vector Yt=Y.Geq(0.5);
153  unsigned int N=Yt.Sum();
154  unsigned int L=Yt.Nel();
155  Pds::Matrix R=Pds::RegressorMatrix(X);
156  Pds::Vector z=Pds::Sigmoid(R*W);
157  Pds::Vector Dz=z.Product(1.0-z);
158 
159  double Na=z.Sum();
160  double N1=Yt.Dot(z);
161  double p1=N1/Na;
162  double p2=(N-N1)/(L-Na);
163 
164  double h1=Pds::Hb(p1);
165  double h2=Pds::Hb(p2);
166  double Dh1=-Pds::Logit2(p1);
167  double Dh2=-Pds::Logit2(p2);
168  /*
169  double q=4.0;
170  double K=Pds::qHbn(0.5,q);
171  double h1=Pds::qHbn(p1,q)/K;
172  double h2=Pds::qHbn(p2,q)/K;
173  double Dh1=Pds::qDHbn(p1,q)/K;
174  double Dh2=Pds::qDHbn(p2,q)/K;
175  */
176  double factor1=(-h1+h2+p1*Dh1-p2*Dh2)/L;
177  double factor2=(-Dh1+Dh2)/L;
178  Pds::Vector DIG= factor1*R.TMul(Dz)+factor2*R.TMul(Dz.Product(Yt));
179 
180  std::cout<<"\n";
181  std::cout<<"N:"<<N<<"\n";
182  std::cout<<"L:"<<L<<"\n";
183  std::cout<<"N1:"<<N1<<"\t N1<Na True positive in Na side\n";
184  std::cout<<"Na:"<<Na<<"\t elems. classify as 1\n";
185  std::cout<<"p1:"<<p1<<"\n";
186  std::cout<<"p2:"<<p2<<"\n";
187  std::cout<<"factor1:"<<factor1<<"\n";
188  std::cout<<"factor2:"<<factor2<<"\n";
189  std::cout<<"IGs:"<<Pds::LogisticModel::CostInformationGainSoft(W,X,Y)<<"\n";
190  std::cout<<"IGh:"<<Pds::LogisticModel::CostInformationGain(W,X,Y)<<"\n";
191  DIG.T().Print("DIG: ");
192 
193  return DIG;
194 }

Hace referencia a CostInformationGain() y CostInformationGainSoft().

Referenciado por FittingGradientIGSoft().

Gráfico de llamadas para esta función:

◆ CostInformationGainSoft()

double Pds::LogisticModel::CostInformationGainSoft ( const Pds::Vector &  W,
const Pds::Matrix &  X,
const Pds::Vector &  Y 
)

Definición en la línea 51 del archivo test_working_FittingGradientIGSoft.cpp.

54 {
55  if(W.IsEmpty()) return Pds::Ra::Nan;
56  if(X.IsEmpty()) return Pds::Ra::Nan;
57  if(Y.IsEmpty()) return Pds::Ra::Nan;
58 
59  if(X.Nlin()!=Y.Nlin()) return Pds::Ra::Nan;
60  if(X.Ncol()!=(W.Nlin()-1)) return Pds::Ra::Nan;
61 
62  Pds::Vector Yh=Y.Geq(0.5);
63 
64  Pds::Vector z=Pds::LogisticModel::Classify(W,X);
65 
66  unsigned int L=Yh.Nlin();
67 
68  double Nt=Yh.Sum();
69  double Na=z.Sum();
70  double N1=Yh.Dot(z);
71 
72  /*
73  // Information gain
74  double Et=Pds::Hb(Nt/L);
75  double E1=Pds::Hb(N1/Na);
76  double val=(Nt-N1)/(L-Na);
77  if(val>1.0) val=1.0;
78  if(val<0) val=0;
79  if(L==Na) val=1;
80  double E0=Pds::Hb(val);
81  */
82 
83  // Gini index
84  double q=2.0;
85  double F=Pds::qHbn(0.5,2.0);
86  double Et=Pds::qHbn(Nt/L,q)/F;
87  double E1=Pds::qHbn(N1/Na,q)/F;
88  double val=(Nt-N1)/(L-Na);
89  if(val>1.0) val=1.0;
90  if(val<0) val=0;
91  if(L==Na) val=1;
92  double E0=Pds::qHbn(val,q)/F;
93 
94 
95 
96  return Et-(Na/L)*E1-((L-Na)/L)*E0;
97 }
Pds::LogisticModel::Classify
Pds::Vector Classify(const Pds::Vector &W, const Pds::Matrix &X)
Calculo del resultado del clasificador.

Hace referencia a Classify().

Referenciado por GradientCostInformationGainSoft() y GradientCostInformationGainSoft2().

Gráfico de llamadas para esta función:

◆ CostXqEntropy()

double Pds::LogisticModel::CostXqEntropy ( const Pds::Vector &  W,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
double  q 
)

Definición en la línea 32 del archivo extra_newhb.h.

36 {
37  if(W.IsEmpty()) return Pds::Ra::Nan;
38  if(X.IsEmpty()) return Pds::Ra::Nan;
39  if(Y.IsEmpty()) return Pds::Ra::Nan;
40 
41  if(X.Nlin()!=Y.Nlin()) return Pds::Ra::Nan;
42  if(X.Ncol()!=(W.Nlin()-1)) return Pds::Ra::Nan;
43 
44  Pds::Vector Yh=Y.Geq(0.5);
45 
46  Pds::Vector z=Pds::LogisticModel::Classify(W,X);
47  z=z.Geq(0.5);
48 
49  unsigned int L=Yh.Nlin();
50 
51  double Np=Yh.Sum();
52  double Na=z.Sum();
53  double N1=Yh.Dot(z);
54 
55  // New entropy 1
56  double E1;
57  if(0==Na) E1=0;
58  else E1=Pds::XqHb(N1/Na,q);
59 
60  // New entropy 0
61  double E0;
62  double P=(Np-N1)/(L-Na);
63  if(P>1.0) P=1.0;
64  if(P<0) P=0.0;
65  if(L==Na) E0=0.0;
66  else E0=Pds::XqHb(P,q);
67 
68 
69  //return pow(Na/L,2)*E1+pow((L-Na)/L,2)*E0;
70  return (Na/L)*E1+((L-Na)/L)*E0;
71 }

Hace referencia a Classify().

Referenciado por GradientCostXqEntropy().

Gráfico de llamadas para esta función:

◆ GradientCostXqEntropy()

Pds::Vector Pds::LogisticModel::GradientCostXqEntropy ( const Pds::Vector &  W,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
double  q,
double  h 
)

Definición en la línea 73 del archivo extra_newhb.h.

78 {
79  if(W.IsEmpty()) return Pds::Vector();
80  if(X.IsEmpty()) return Pds::Vector();
81  if(Y.IsEmpty()) return Pds::Vector();
82 
83  if(X.Nlin()!=Y.Nlin()) return Pds::Vector();
84  if(X.Ncol()!=(W.Nlin()-1)) return Pds::Vector();
85 
86  if(h==0.0) return Pds::Vector();
87 
88  unsigned int N=W.Nel();
89 
90  Pds::Vector D(N);
91  Pds::Vector Whp(N);
92  Pds::Vector Whm(N);
93  double dn;
94 
95  Whp.Copy(W);
96  Whm.Copy(W);
97 
98  for(unsigned int n=0;n<N;n++)
99  {
100  Whp.SetRaw(n,W.GetRaw(n)+h);
101  Whm.SetRaw(n,W.GetRaw(n)-h);
102 
103  dn=( Pds::LogisticModel::CostXqEntropy(Whp,X,Y,q)
104  -Pds::LogisticModel::CostXqEntropy(Whm,X,Y,q) )/(2*h);
105 
106  D.SetRaw(n,dn);
107 
108  Whp.SetRaw(n,W.GetRaw(n));
109  Whm.SetRaw(n,W.GetRaw(n));
110  }
111  return D;
112 }
Pds::LogisticModel::CostXqEntropy
double CostXqEntropy(const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y, double q)
Definition: extra_newhb.h:32

Hace referencia a CostXqEntropy().

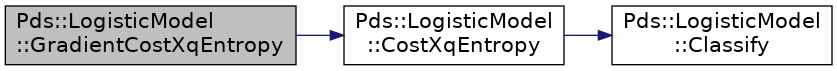
Gráfico de llamadas para esta función:

◆ GradientCostXqEntropySoft()

Pds::Vector Pds::LogisticModel::GradientCostXqEntropySoft ( const Pds::Vector &  W,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
double  q 
)

Definición en la línea 114 del archivo extra_newhb.h.

118 {
119  if(W.IsEmpty()) return Pds::Vector();
120  if(X.IsEmpty()) return Pds::Vector();
121  if(Y.IsEmpty()) return Pds::Vector();
122 
123  if(X.Nlin()!=Y.Nlin()) return Pds::Vector();
124  if(X.Ncol()!=(W.Nlin()-1)) return Pds::Vector();
125 
126  Pds::Vector Yt=Y.Geq(0.5);
127  unsigned int N=Yt.Sum();// numero total de 1s
128  unsigned int L=Yt.Nel();// numero de elementos
129 
130  Pds::Matrix R=Pds::RegressorMatrix(X);
131  Pds::Vector z=Pds::Sigmoid(R*W);
132  Pds::Vector Dz=z.Product(1.0-z);
133 
134  double Na=z.Sum();
135  double N1=Yt.Dot(z);
136  double p1=N1/Na;
137  double p2=(N-N1)/(L-Na);
138 
139  double h1=Pds::XqHb(p1,q);
140  double h2=Pds::XqHb(p2,q);
141  double Dh1=Pds::DXqHb(p1,q);
142  double Dh2=Pds::DXqHb(p2,q);
143 
144  double factor1=-(-h1+h2+p1*Dh1-p2*Dh2)/L;
145  double factor2=-(-Dh1+Dh2)/L;
146  Pds::Vector Der= factor1*R.TMul(Dz)+factor2*R.TMul(Dz.Product(Yt));
147 
148  return Der;
149 }

Enlaces de interés

HomePage Bazaar Download Bug report Ayuda Developer Feed
Manual de referencia generado el Domingo, 28 de Noviembre de 2021 13:03:57 para la biblioteca libpdsmlmm usando  Generado el Domingo, 28 de Noviembre de 2021 13:03:57 para libpdsmlmm por   doxygen 1.9.2