Home | Develop | Download | Contact
Namespaces
Funciones en el namespace Pds::LogisticModel
Clasificadores » Clasificadores – Funciones

Funciones para trabajar con "Logistic Regression": Pds::LogisticModel::FittingGradientSVM(), Pds::LogisticModel::Classify(), etc. Más...

Namespaces

namespace  Pds
 Nombre de espacio para Pds (Procesamiento Digital de Senales)
 
namespace  Pds::LogisticModel
 Nombre de espacio para LogisticModel (Logistic regression)
 

Logistic regression : Clasificador

Pds::Vector Pds::LogisticModel::Classify (const Pds::Vector &W, const Pds::Matrix &X)
 Calculo del resultado del clasificador. Más...
 

Logistic regression : Función de costo

double Pds::LogisticModel::CostInformationGain (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y)
 Calculo de costo. Más...
 
Pds::Vector Pds::LogisticModel::GradientCostInformationGain (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y, double h)
 Calculo de costo. Más...
 
double Pds::LogisticModel::CostCrossEntropy (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y)
 Calculo de pesos. Más...
 
double Pds::LogisticModel::CostMeanSquare (const Pds::Vector &W, const Pds::Matrix &X, const Pds::Vector &Y)
 Calculo de pesos. Más...
 

Logistic regression : Peso inicial

Pds::Vector Pds::LogisticModel::GetW0MeanMethod (const Pds::Matrix &X)
 Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica. Más...
 
Pds::Vector Pds::LogisticModel::GetW0CornerMeanMethod (const Pds::Matrix &X, double Delta=0.001)
 Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica. Más...
 
Pds::Vector Pds::LogisticModel::GetW0MeanSquareMethod (const Pds::Matrix &X)
 Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica. Más...
 

Logistic regression : Regresión de pesos : Familia Mean Square

Pds::Vector Pds::LogisticModel::FittingLogitMeanSquare (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, double Delta=0.0001)
 Calculo de pesos. Más...
 
Pds::Vector Pds::LogisticModel::FittingLogitMeanSquare (const Pds::Matrix &X, const Pds::Vector &Y, double Delta=0.0001)
 Calculo de pesos. Más...
 
Pds::Vector Pds::LogisticModel::FittingLogitWeightedMeanSquare (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &D, double Delta=0.0001)
 Calculo de pesos. Más...
 
Pds::Vector Pds::LogisticModel::FittingLogitWeightedMeanSquare (const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &D, double Delta=0.0001)
 Calculo de pesos. Más...
 

Logistic regression : Regresión de pesos : Familia Robust Mean Square

Pds::Vector Pds::LogisticModel::FittingRobustLogitMeanSquare (const Pds::Matrix &X, const Pds::Vector &Y, double Delta=0.0001, unsigned int N=2, double Offset=0.1)
 Calculo de pesos. Más...
 
Pds::Vector Pds::LogisticModel::FittingRobustLogitMeanSquare (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, double Delta=0.0001, unsigned int N=2, double Offset=0.1)
 Calculo de pesos. Más...
 

Logistic regression : Regresión de pesos : Familia Cross Entropy

Pds::Vector Pds::LogisticModel::FittingGradientCrossEntropy (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &W0)
 Gradiente descendente para sigmoide. Más...
 
Pds::Vector Pds::LogisticModel::FittingGradientSVM (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &W0)
 Gradiente descendente para sigmoide. Más...
 

Logistic regression : Regresión de pesos : Familia Information Gain

Pds::Vector Pds::LogisticModel::FittingOrtogonalIG (const Pds::Matrix &X, const Pds::Vector &Y, unsigned int MinID)
 Calculo de pesos. Más...
 
Pds::Vector Pds::LogisticModel::FittingGradientIG (Pds::IterationConf &Conf, const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &W0)
 Calculo de pesos. Más...
 
Pds::Vector Pds::LogisticModel::FittingParrallelPlaneIS (const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &W0, double *ISmin=NULL, double Delta=0.001)
 Calculo de pesos buscando el plano paralelo a W0 que genere la menor suma de informaciones en la particion, es equivalente a buscar la mayor information gain. Más...
 

Logistic regression : Funciones de ajuste

Pds::Vector Pds::LogisticModel::FittingByFactor (const Pds::Matrix &X, const Pds::Vector &Y, const Pds::Vector &W0, double Delta=0.001)
 Aplica la teoria de Logit MeanSquare para ajustar W0 por um factor real adecuado. Más...
 

Logistic regression : Funciones de diagnóstico

Pds::DataErrorCurve Pds::LogisticModel::LearningCurves (Pds::IterationConf &Conf, const Pds::Matrix &Xtr, const Pds::Vector &Ytr, const Pds::Matrix &Xcv, const Pds::Vector &Ycv, double percent)
 Retorna learning curve. Más...
 

Descripción detallada

Funciones para trabajar con "Logistic Regression": Pds::LogisticModel::FittingGradientSVM(), Pds::LogisticModel::Classify(), etc.

#include <Pds/FuncLogisticModel>

Documentación de las funciones

◆ Classify()

Pds::Vector Pds::LogisticModel::Classify ( const Pds::Vector &  W,
const Pds::Matrix &  X 
)

Calculo del resultado del clasificador.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad h_{\mathbf{w}}\left(\mathbf{X}\right)=Sigmoid([1~\mathbf{X}]\mathbf{w}) \]

Parámetros
[in]WVector de pesos.
[in]XMatriz con los vectores de datos (muestras) en las lineas.
Devuelve
El resultado del clasificador.
Ejemplos
example_logisticregression_ce.cpp, example_logisticregression_ce_svm_hard.cpp, example_logisticregression_ig.cpp, example_logisticregression_ig2.cpp, example_logisticregression_kmeanstest.cpp, example_logisticregression_ms.cpp, example_logisticregression_paris.cpp, example_logisticregression_robust_meansquare.cpp, example_logisticregression_svm.cpp y example_logisticregression_w0.cpp.

Referenciado por Pds::LogisticModel::CostInformationGainSoft() y Pds::LogisticModel::CostXqEntropy().

◆ CostInformationGain()

double Pds::LogisticModel::CostInformationGain ( const Pds::Vector &  W,
const Pds::Matrix &  X,
const Pds::Vector &  Y 
)

Calculo de costo.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad \mathbf{y} =\left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right) \qquad \rightarrow \qquad \mathbf{u} =\left(\begin{matrix} 1\\ 1\\ \vdots\\ 1\\ \end{matrix}\right) \]

\[ \mathbf{z}\left(\mathbf{w}\right)=Sigmoid\left(\left[\overline{1}~\mathbf{X}\right]\mathbf{w}\right), \quad \mathbf{\bar{z}}\left(\mathbf{w}\right)=round(\mathbf{z}) \]

Calculado desde el punto de vista matemático

\[ N_t=\mathbf{u}^{T}\mathbf{y}, \quad N_a\left(\mathbf{w}\right)= \mathbf{u}^{T}\mathbf{\bar{z}}\left(\mathbf{w}\right) \quad N_1\left(\mathbf{w}\right)= \mathbf{y}^{T}\mathbf{\bar{z}}\left(\mathbf{w}\right) \]

\[ Cost\left(\mathbf{w}\right) \quad = \quad h_b \left(\frac{N_t}{L}\right) -\frac{N_a\left(\mathbf{w}\right)}{L}~h_b \left(\frac{N_1\left(\mathbf{w}\right)}{N_a\left(\mathbf{w}\right)}\right) -\frac{L-N_a\left(\mathbf{w}\right)}{L}~h_b \left(\frac{N_t-N_1\left(\mathbf{w}\right)}{L-N_a\left(\mathbf{w}\right)}\right) \]

Calculado desde el punto de vista programático

\[ \mathbf{\hat{y}} =\left(\begin{matrix} \mathbf{y}_{0}\\ \mathbf{y}_{1} \end{matrix}\right), \quad \mathbf{y}_{0}=\mathbf{y}_{\mathbf{\bar{z}}\equiv \bar{0}}, \quad \mathbf{y}_{1}=\mathbf{y}_{\mathbf{\bar{z}}\equiv \bar{1}} \]

\[ Cost\left(\mathbf{w}\right) \quad = \quad h_b \left(p_{\mathbf{\hat{y}}}\right) -\frac{N_{\mathbf{y}_{1}}}{L}~h_b \left(p_{\mathbf{y}_1}\right) -\frac{N_{\mathbf{y}_{0}}}{L}~h_b \left(p_{\mathbf{y}_0}\right) \]

$p_{\mathbf{y}_0}$ es la probabilidad de 1s en el vector $\mathbf{y}_0$
$N_{\mathbf{y}_0}$ es el número de elementos en el vector $\mathbf{y}_0$
$p_{\mathbf{y}_1}$ es la probabilidad de 1s en el vector $\mathbf{y}_1$
$N_{\mathbf{y}_1}$ es el número de elementos en el vector $\mathbf{y}_1$

Parámetros
[in]WVector de pesos.
[in]XMatriz con los vectores de datos (muestras) en las lineas.
[in]YVector de datos de salida.
Devuelve
El valor de la funcion de costo usando Information Gain.
Ejemplos
example_logisticregression_cost.cpp, example_logisticregression_ig.cpp y example_logisticregression_ig2.cpp.

Referenciado por Pds::LogisticModel::FittingGradientIGSoft() y Pds::LogisticModel::GradientCostInformationGainSoft2().

◆ GradientCostInformationGain()

Pds::Vector Pds::LogisticModel::GradientCostInformationGain ( const Pds::Vector &  W,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
double  h 
)

Calculo de costo.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad \mathbf{y} =\left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right), \qquad \mathbf{w} =\left(\begin{matrix} w_0\\ w_1\\ \vdots\\ w_N\\ \end{matrix}\right) \]

\[ C(\mathbf{w})\equiv Pds::LogisticModel::CostInformationGain(\mathbf{w},\mathbf{X},\mathbf{y}) \]

\[ \mathbf{h}_n =(0,0,...,0,...,0,0), \quad \mathbf{h}_n(n)=h; \]

\[ \nabla C(\mathbf{w}) \equiv \frac{\partial C(\mathbf{w})}{\partial \mathbf{w}} \equiv \left(\begin{matrix} \frac{\partial C(\mathbf{w})}{\partial w_0}\\ \frac{\partial C(\mathbf{w})}{\partial w_1}\\ \vdots\\ \frac{\partial C(\mathbf{w})}{\partial w_N}\\ \end{matrix}\right) \approx \left(\begin{matrix} \frac{ C(\mathbf{w}+\mathbf{h}_0) - C(\mathbf{w}-\mathbf{h}_0)}{2h}\\ \frac{ C(\mathbf{w}+\mathbf{h}_1) - C(\mathbf{w}-\mathbf{h}_1)}{2h}\\ \vdots\\ \frac{ C(\mathbf{w}+\mathbf{h}_N) - C(\mathbf{w}-\mathbf{h}_N)}{2h}\\ \end{matrix}\right) \]

Parámetros
[in]WVector de pesos.
[in]XMatriz con los vectores de datos (muestras) en las lineas.
[in]YVector de datos de salida.
[in]hPaso para aplicar la.
Devuelve
Un vector con el gradiente en relacion a W de la funcion Pds::LogisticModel::CostInformationGain().

◆ CostCrossEntropy()

double Pds::LogisticModel::CostCrossEntropy ( const Pds::Vector &  W,
const Pds::Matrix &  X,
const Pds::Vector &  Y 
)

Calculo de pesos.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad \mathbf{y} =\left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right), \qquad \rightarrow \qquad h_{\mathbf{w}}\left(\mathbf{x}^{T}\right)=Sigmoid\left(\left[\overline{1}~\mathbf{X}\right]\mathbf{w}\right) \]

\[ Cost\left(\mathbf{w}\right) \quad = \quad \frac{1}{L}\sum \limits_{i}^{L} -y_{i}~log_2\left(h_{\mathbf{w}}\left(\mathbf{x}_{i}^{T}\right)\right) - \left(1-y_{i}\right)~log_2\left(1-h_{\mathbf{w}}\left(\mathbf{x}_{i}^{T}\right)\right) \]

Parámetros
[in]WVector de pesos.
[in]XMatriz con los vectores de datos (muestras) en las lineas.
[in]YVector de datos de salida.
Devuelve
El valor de la funcion de costo usando Cross Entropy.

◆ CostMeanSquare()

double Pds::LogisticModel::CostMeanSquare ( const Pds::Vector &  W,
const Pds::Matrix &  X,
const Pds::Vector &  Y 
)

Calculo de pesos.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad \mathbf{y} =\left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right), \qquad \rightarrow \qquad h_{\mathbf{w}}\left(\mathbf{X}\right)=Sigmoid\left(\left[\overline{1}~\mathbf{X}\right]\mathbf{w}\right) \]

\[ Cost\left(\mathbf{w}\right) = \frac{1}{L}||h_{\mathbf{w}}\left(\mathbf{X}\right)-\mathbf{y}||^2 = \frac{1}{L}\sum \limits_{i}^{L} \left(h_{\mathbf{w}}\left(\mathbf{x}_i^{T}\right)-y_i\right)^2 \]

Parámetros
[in]WVector de pesos.
[in]XMatriz con los vectores de datos (muestras) en las lineas.
[in]YVector de datos de salida.
Devuelve
El valor de la funcion de costo usando Mean Square.

◆ GetW0MeanMethod()

Pds::Vector Pds::LogisticModel::GetW0MeanMethod ( const Pds::Matrix &  X)

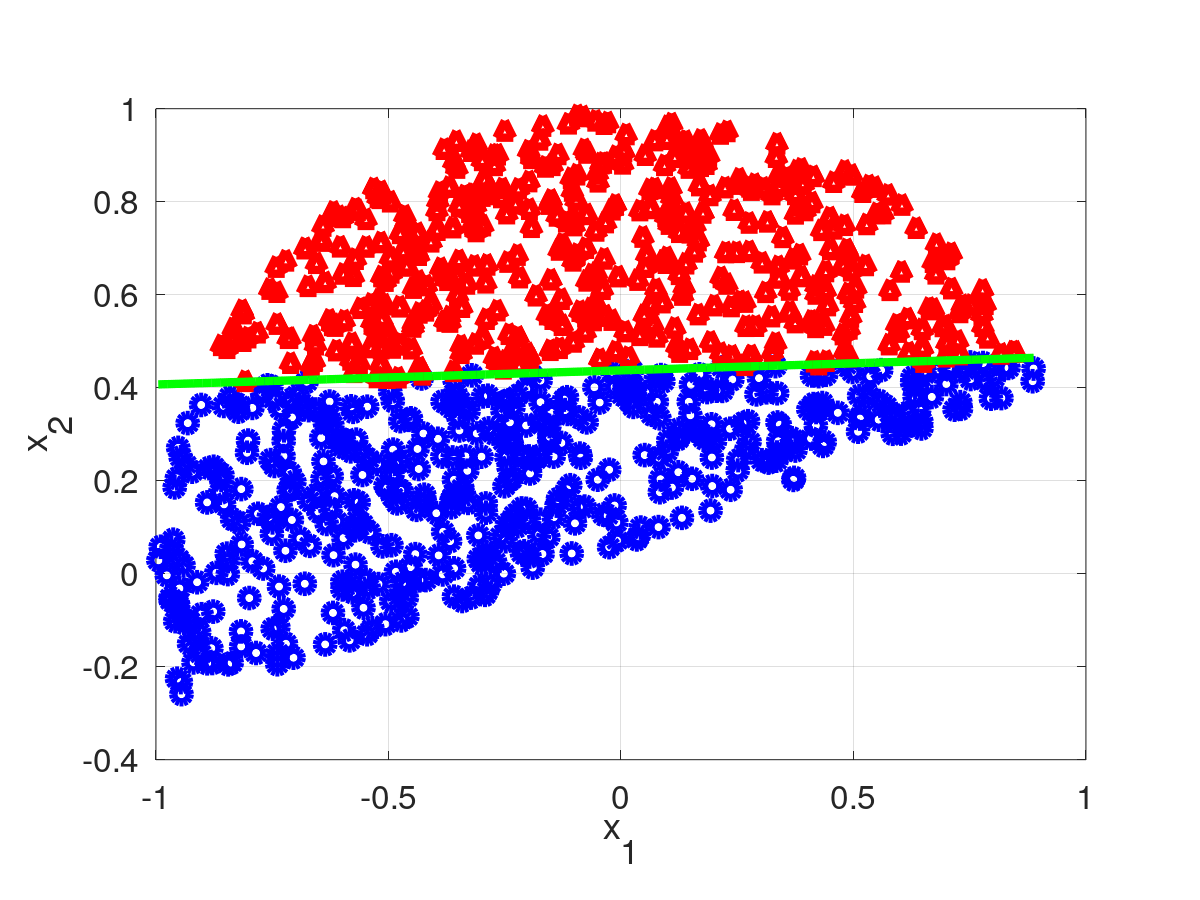
Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica.

Coloca el hiperplano en el punto medio de las muestras, dejando aleatoriamente selecionada la direción del hiperplano.

GetW0MeanMethod()

\[z=mean\_of\_columns(X),\qquad N=X.Ncol()\equiv z.Nel()\]

\[\mathbf{z}=[z_1,~z_2,~...,z_N]^T\]

\[\mathbf{w}=[w_0,~w_1,~...,w_N]^T\]

\[w_1=randn();~w_2=randn();~...;~w_N=randn();\qquad w_{0}=-\sum_{n=1}^{N} z_{i} w_{i}\]

\[\mathbf{w}\leftarrow\frac{\mathbf{w}}{|\mathbf{w}|}\]

Parámetros
[in]XVector de datos $\mathbf{X}$.
Devuelve
Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica.
Ejemplos
example_logisticregression_cost.cpp, example_logisticregression_ig.cpp, example_logisticregression_paris.cpp y example_logisticregression_w0.cpp.

◆ GetW0CornerMeanMethod()

Pds::Vector Pds::LogisticModel::GetW0CornerMeanMethod ( const Pds::Matrix &  X,
double  Delta = 0.001 
)

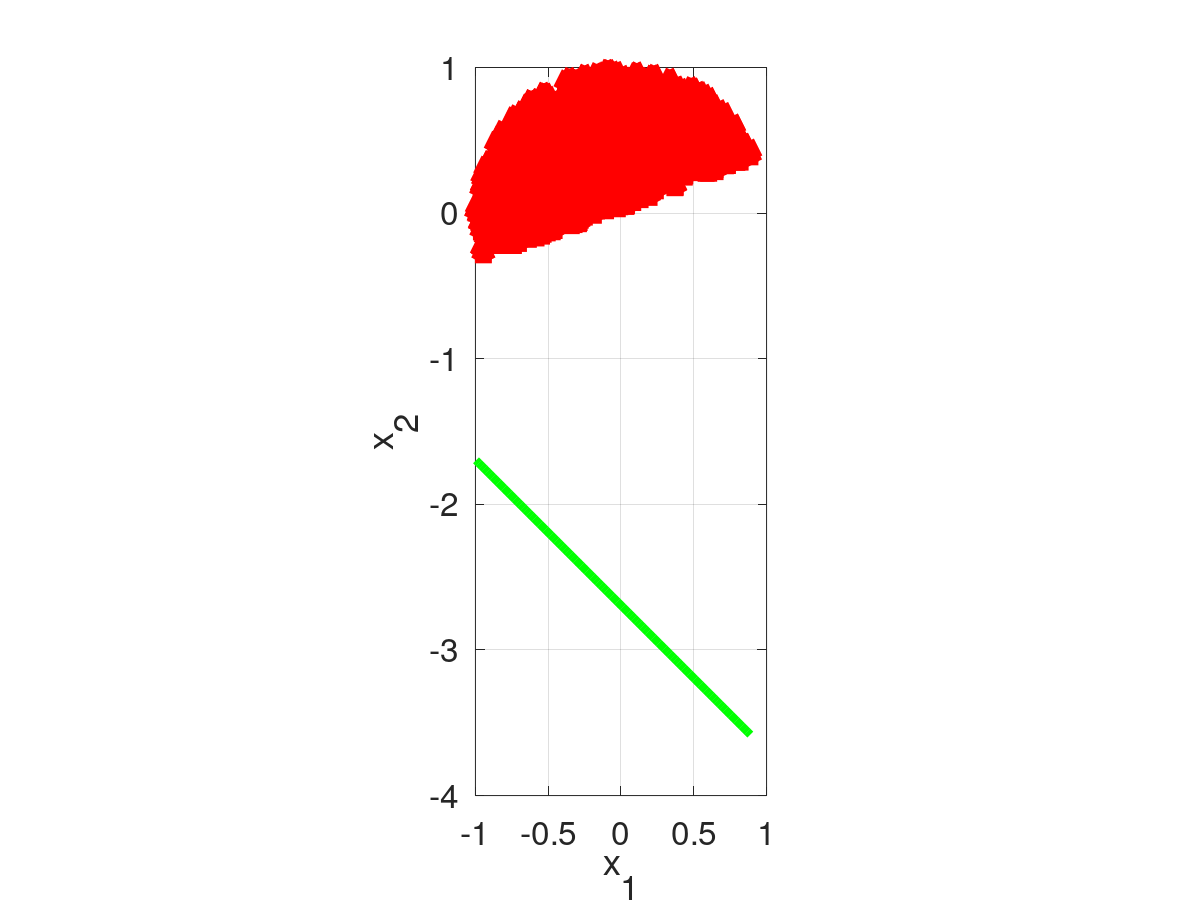
Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica.

Coloca la linea de modo que todos los puntos son positivos (1).

GetW0CornerMeanMethod()

\[z=mean\_of\_columns(X),\qquad N=X.Ncol()\equiv z.Nel()\]

\[\mathbf{w}=[w_0,~w_1,~...,w_N]^T\]

\[w_{0}=-\sum_{n=1}^{N} z_{i},\qquad w_1=w_2=...w_N=1\]

Parámetros
[in]XVector de datos $\mathbf{X}$.
[in]DeltaFactor de ajuste final.
Devuelve
Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica.
Ejemplos
example_logisticregression_w0.cpp.

Referenciado por Pds::LogisticModel::FittingGradientIGSoft().

◆ GetW0MeanSquareMethod()

Pds::Vector Pds::LogisticModel::GetW0MeanSquareMethod ( const Pds::Matrix &  X)

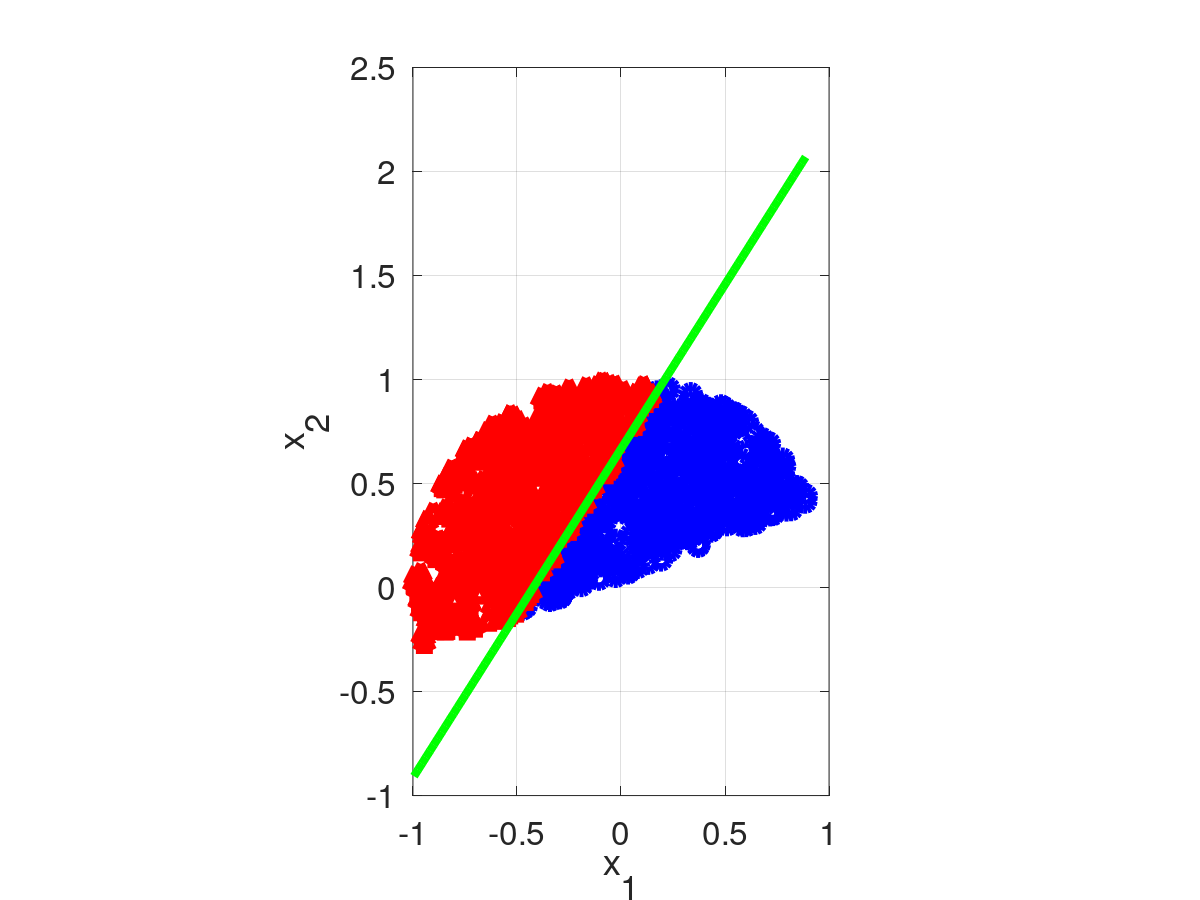
Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica.

Encaja un plano dentro de la nuve de puntos, bajo la perspectiva de que $x_1$ es el contradominio del dominio $\{x_2,x_3,...,x_N\}$.

GetW0CornerMeanMethod()

\[si~\mathbf{X}=[\mathbf{x}_1,~\mathbf{x}_2,~...,~\mathbf{x}_N]\]

\[\mathbf{R}=[\mathbf{1},~\mathbf{x}_2,~\mathbf{x}_3,~...,~\mathbf{x}_N]\]

\[\mathbf{v}=(\mathbf{R}^T\mathbf{R})^{-1}\mathbf{R}^T\mathbf{x}_1\]

\[\mathbf{v}=[v_1,~v_2,~v_3,~...,~v_N]\]

\[\mathbf{W}=[v_1,~-1,~v_2,~v_3,~...,~v_N]\]

Parámetros
[in]XVector de datos $\mathbf{X}$.
Devuelve
Obtiene de forma rapida un vector $\mathbf{w}$ inicial para usar en regresion logistica.
Ejemplos
example_logisticregression_ce.cpp, example_logisticregression_ce_svm_hard.cpp, example_logisticregression_cost.cpp y example_logisticregression_w0.cpp.

◆ FittingLogitMeanSquare() [1/2]

Pds::Vector Pds::LogisticModel::FittingLogitMeanSquare ( Pds::IterationConf &  Conf,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
double  Delta = 0.0001 
)

Calculo de pesos.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad \mathbf{y} =\left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right), \qquad \rightarrow \qquad \mathbf{R} = \left(\begin{matrix} 1 & \mathbf{X}\\ \end{matrix}\right), \qquad \mathbf{y_o} = \delta+(1-2 \delta)\mathbf{y}. \]

\[ \begin{array}{l} if(rcond>=Pds::Ml::WarningRCond) \\ \qquad \mathbf{w} = \left(\mathbf{R}^{T}\mathbf{R}\right)^{-1} \mathbf{R}^{T} logit(\mathbf{y_o})\\ \qquad with \qquad Cost(\mathbf{w}) \equiv \frac{1}{L}||\mathbf{R}\mathbf{w}-logit(\mathbf{y_o})||^2 \\ else\\ \qquad \mathbf{w} \leftarrow \mathbf{w} +\left(\mathbf{R}^{T}\mathbf{R}+\frac{\gamma L}{N}\mathbf{I}\right)^{-1} \left(\mathbf{R}^{T} logit(\mathbf{y_o})-\mathbf{R}^{T}\mathbf{R} \mathbf{w} \right)\\ \qquad with \qquad Cost(\mathbf{w}) \equiv \frac{1}{L}||\mathbf{R}\mathbf{w}-logit(\mathbf{y_o})||^2+\frac{\gamma}{N}||\mathbf{w}-\mathbf{w}_{last}||^2 \end{array} \]

Parámetros
[in]ConfConfiguraciones para algun algoritmo que itera.
[in]XVector de datos $\mathbf{X}$.
[in]YVector de datos $\mathbf{y}$.
[in]DeltaValor $\delta$.
Devuelve
Un vector de pesos $\mathbf{w}$ si el calculo es posible o una vacio si no existe inversa de $\mathbf{R}^{T}\mathbf{R}$.
Ejemplos
example_logisticregression_meansquare_hard.cpp y example_logisticregression_ms.cpp.

◆ FittingLogitMeanSquare() [2/2]

Pds::Vector Pds::LogisticModel::FittingLogitMeanSquare ( const Pds::Matrix &  X,
const Pds::Vector &  Y,
double  Delta = 0.0001 
)

Calculo de pesos.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad \mathbf{y} = \left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right), \]

\[ \mathbf{R} = \left(\begin{matrix} 1 & \mathbf{X}\\ \end{matrix}\right), \qquad \mathbf{y_o} = \delta+(1-2 \delta)\mathbf{y}, \qquad Cost(\mathbf{w}) \equiv \frac{1}{L}||\mathbf{R}\mathbf{w}-logit(\mathbf{y_o})||^2. \]

\[ \begin{array}{l} if(rcond>=Pds::Ml::WarningRCond) \\ \qquad \mathbf{w} = \left(\mathbf{R}^{T}\mathbf{R}\right)^{-1} \mathbf{R}^{T} logit(\mathbf{y_o}) \\ else\\ \qquad \mathbf{w} = [] \end{array} \]

Parámetros
[in]XVector de datos $\mathbf{X}$.
[in]YVector de datos $\mathbf{y}$.
[in]DeltaValor $\delta$.
Devuelve
Un vector de pesos $\mathbf{w}$ si el calculo es posible o una vacio si no existe inversa de $\mathbf{R}^{T}\mathbf{R}$.

◆ FittingLogitWeightedMeanSquare() [1/2]

Pds::Vector Pds::LogisticModel::FittingLogitWeightedMeanSquare ( Pds::IterationConf &  Conf,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
const Pds::Vector &  D,
double  Delta = 0.0001 
)

Calculo de pesos.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad \mathbf{y} =\left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right), \qquad \rightarrow \qquad \mathbf{R} = \left(\begin{matrix} 1 & \mathbf{X}\\ \end{matrix}\right), \qquad \mathbf{y_o} = \delta+(1-2 \delta)\mathbf{y}. \]

\[ ||\mathbf{b}||^2_{\mathbf{A}}\equiv \mathbf{b}^{T}\mathbf{A}\mathbf{b} \]

\[ \begin{array}{l} if(rcond>=Pds::Ml::WarningRCond) \\ \qquad \mathbf{w} = \left(\mathbf{R}^{T} \mathbf{A} \mathbf{R}\right)^{-1} \mathbf{R}^{T} \mathbf{A} logit(\mathbf{y_o})\\ \qquad with \qquad Cost(\mathbf{w}) \equiv \frac{1}{L}||\mathbf{R}\mathbf{w}-logit(\mathbf{y_o})||^2_{\mathbf{A}} \\ else\\ \qquad \mathbf{w} \leftarrow \mathbf{w} +\left(\mathbf{R}^{T} \mathbf{A} \mathbf{R}+\frac{\gamma L}{N}\mathbf{I}\right)^{-1} \left(\mathbf{R}^{T} \mathbf{A} logit(\mathbf{y_o})-\mathbf{R}^{T}\mathbf{R} \mathbf{w} \right)\\ \qquad with \qquad Cost(\mathbf{w}) \equiv \frac{1}{L}||\mathbf{R}\mathbf{w}-logit(\mathbf{y_o})||^2_{\mathbf{A}}+\frac{\gamma}{N}||\mathbf{w}-\mathbf{w}_{last}||^2 \end{array} \]

Parámetros
[in]ConfConfiguraciones para algun algoritmo que itera.
[in]XVector de datos $\mathbf{X}$.
[in]YVector de datos $\mathbf{y}$.
[in]DVector $\mathbf{d}$ para formar $\mathbf{A}=diag(\mathbf{d})^T diag(\mathbf{d}) $.
[in]DeltaValor $\delta$.
Devuelve
Un vector de pesos $\mathbf{w}$ si el calculo es posible o una vacio si no existe inversa de $\mathbf{R}^{T}\mathbf{R}$.
Ejemplos
example_logisticregression_meansquare_hard.cpp.

◆ FittingLogitWeightedMeanSquare() [2/2]

Pds::Vector Pds::LogisticModel::FittingLogitWeightedMeanSquare ( const Pds::Matrix &  X,
const Pds::Vector &  Y,
const Pds::Vector &  D,
double  Delta = 0.0001 
)

Calculo de pesos.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad \mathbf{y} = \left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right), \qquad \mathbf{A}=diag(\mathbf{d})^T diag(\mathbf{d}) \]

\[ ||\mathbf{b}||^2_{\mathbf{A}}\equiv \mathbf{b}^{T}\mathbf{A}\mathbf{b} \]

\[ \mathbf{R} = \left(\begin{matrix} 1 & \mathbf{X}\\ \end{matrix}\right), \qquad \mathbf{y_o} = \delta+(1-2 \delta)\mathbf{y}, \qquad Cost(\mathbf{w}) \equiv \frac{1}{L}||\mathbf{R}\mathbf{w}-logit(\mathbf{y_o})||^2_{\mathbf{A}}. \]

\[ \begin{array}{l} if(rcond>=Pds::Ml::WarningRCond) \\ \qquad \mathbf{w} = \left(\mathbf{R}^{T}\mathbf{A}\mathbf{R}\right)^{-1} \mathbf{R}^{T} \mathbf{A} logit(\mathbf{y_o}) \\ else\\ \qquad \mathbf{w} = [] \end{array} \]

Parámetros
[in]XVector de datos $\mathbf{X}$.
[in]YVector de datos $\mathbf{y}$.
[in]DVector $\mathbf{d}$ para formar $\mathbf{A}=diag(\mathbf{d})^T diag(\mathbf{d}) $.
[in]DeltaValor $\delta$.
Devuelve
Un vector de pesos $\mathbf{w}$ si el calculo es posible o una vacio si no existe inversa de $\mathbf{R}^{T}\mathbf{R}$.

◆ FittingRobustLogitMeanSquare() [1/2]

Pds::Vector Pds::LogisticModel::FittingRobustLogitMeanSquare ( const Pds::Matrix &  X,
const Pds::Vector &  Y,
double  Delta = 0.0001,
unsigned int  N = 2,
double  Offset = 0.1 
)

Calculo de pesos.

\[ \begin{array}{l} W=Pds::LogisticModel::FittingLogitMeanSquare(X,Y,Delta);\\ for(n=0;n<N;n++)\\ \{\\ \qquad Yr=Pds::LogisticModel::Classify(W,X);\\ \qquad D=\frac{1}{|Y-hard\{Yr\}|+Offset}\\ \qquad W=Pds::LogisticModel::FittingLogitWeightedMeanSquare(X,Y,D,Delta);\\ \} \end{array} \]

Parámetros
[in]XVector de datos $\mathbf{X}$.
[in]YVector de datos $\mathbf{y}$.
[in]DeltaValor $\delta$.
[in]NPasadas de weighted mean square method. N==0 desactiva la etapa robusta.
[in]OffsetOffset en los pesos.
Devuelve
Un vector de pesos $\mathbf{w}$ si el calculo es posible o una vacio si no.
Ejemplos
example_logisticregression_robust_meansquare.cpp.

◆ FittingRobustLogitMeanSquare() [2/2]

Pds::Vector Pds::LogisticModel::FittingRobustLogitMeanSquare ( Pds::IterationConf &  Conf,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
double  Delta = 0.0001,
unsigned int  N = 2,
double  Offset = 0.1 
)

Calculo de pesos.

\[ \begin{array}{l} W=Pds::LogisticModel::FittingLogitMeanSquare(Conf,X,Y,Delta);\\ for(n=0;n<N;n++)\\ \{\\ \qquad Yr=Pds::LogisticModel::Classify(W,X);\\ \qquad D=\frac{1}{|Y-hard\{Yr\}|+Offset}\\ \qquad W=Pds::LogisticModel::FittingLogitWeightedMeanSquare(Conf,X,Y,D,Delta);\\ \} \end{array} \]

Parámetros
[in]ConfConfiguraciones para algun algoritmo que itera.
[in]XVector de datos $\mathbf{X}$.
[in]YVector de datos $\mathbf{y}$.
[in]DeltaValor $\delta$.
[in]NPasadas de weighted mean square method. N==0 desactiva la etapa robusta.
[in]OffsetOffset en los pesos.
Devuelve
Un vector de pesos $\mathbf{w}$ si el calculo es posible o una vacio si no.

◆ FittingGradientCrossEntropy()

Pds::Vector Pds::LogisticModel::FittingGradientCrossEntropy ( Pds::IterationConf &  Conf,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
const Pds::Vector &  W0 
)

Gradiente descendente para sigmoide.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad \mathbf{y} = \left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right), \]

\[ \mathbf{R} = [\mathbf{1}\quad \mathbf{X}], \qquad h_{\mathbf{w}}(\mathbf{X}) \leftarrow Sigmoid(\mathbf{R} \mathbf{w}), \qquad \mathbf{I}_b= \left(\begin{matrix} 0 & 0 & 0 & ... & 0\\ 0 & 1 & 0 & ... & 0\\ 0 & 0 & 1 & ... & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & ... & 1 \end{matrix}\right) \]

\[ Cost\left(\mathbf{w}\right) = \frac{1}{L}\sum \limits_{i}^{L} \left\{ -y_{i} ~ log_2\left(h_{\mathbf{w}}\left(\mathbf{x}_{i}^{T}\right)\right) ~ - \left(1-y_{i}\right) ~ log_2\left(1-h_{\mathbf{w}}\left(\mathbf{x}_{i}^{T}\right)\right) \right\} \qquad +\qquad \frac{\lambda}{2N}||\mathbf{I}_b\mathbf{w}||^2 \]

\[ Repetir: \qquad \mathbf{w} \leftarrow \mathbf{w} - \alpha \left\{ \frac{1}{L} \mathbf{R}^{T} \left( h_{\mathbf{w}}(\mathbf{X})-\mathbf{y} \right) \quad + \quad \frac{\lambda}{N} \mathbf{I}_b\mathbf{w} \right\}. \]

Parámetros
[in]ConfValores de configuracion de la iteracion.
[in]XMatriz con los vectores de datos (muestras) en las lineas.
[in]YVector resultados $\mathbf{y}$.
[in]W0Primeiro valor de $\mathbf{w}$.
Devuelve
Unvector de pesos.
Ejemplos
example_logisticregression_ce.cpp y example_logisticregression_ce_svm_hard.cpp.

◆ FittingGradientSVM()

Pds::Vector Pds::LogisticModel::FittingGradientSVM ( Pds::IterationConf &  Conf,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
const Pds::Vector &  W0 
)

Gradiente descendente para sigmoide.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad \mathbf{y} = \left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right), \]

\[ \mathbf{\hat{y}}=2\mathbf{y}-1, \qquad \mathbf{R} = [\mathbf{1}\quad \mathbf{X}], \qquad \mathbf{r}^{T} = [\mathbf{1}\quad \mathbf{x}^{T}], \qquad \mathbf{I}_b= \left(\begin{matrix} 0 & 0 & 0 & ... & 0\\ 0 & 1 & 0 & ... & 0\\ 0 & 0 & 1 & ... & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & ... & 1 \end{matrix}\right) \]

\[ \begin{matrix} Cost\left(\mathbf{w}\right) & = & \frac{1}{L}\sum \limits_{i}^{L} \left\{ y_{i} ~ Cost_{1}\left(\mathbf{r}^{T}\mathbf{w}\right) ~ + \left(1-y_{i}\right) ~ Cost_{0}\left(\mathbf{r}^{T}\mathbf{w}\right) \right\} & + & \frac{\lambda}{2N}||\mathbf{I}_b\mathbf{w}||^2\\ ~ & = & \frac{1}{L}\sum \limits_{i}^{L} Max\{0,1-\hat{y}_{i}\mathbf{r}^{T}\mathbf{w}\} & + & \frac{\lambda}{2N}||\mathbf{I}_b\mathbf{w}||^2\\ \end{matrix} \]

\[ -log\left(\frac{1}{1+e^{-z}}\right) \approx Cost_{1}\left(z\right)=Cost_{0}\left(-z\right) = (1-z)(0\leq (1-z)) \]

\[ \frac{\partial Max\{0,1-(2 y-1) z \} }{\partial z} \equiv \phi_{y}(z)= \left\{ \begin{matrix} -y & ; & z<-1\\ 1-2y & ; & -1 \leq z \leq +1\\ 1-y & ; & +1 \leq z \end{matrix} \right. \]

\[ Repetir: \qquad \mathbf{w} \leftarrow \mathbf{w} - \alpha \left\{ \frac{1}{L} \mathbf{R}^{T} \phi_{\mathbf{y}}(\mathbf{R}\mathbf{w}) \quad + \quad \frac{\lambda}{N} \mathbf{I}_b\mathbf{w} \right\}. \]

Parámetros
[in]ConfValores de configuracion de la iteracion.
[in]XMatriz con los vectores de datos (muestras) en las lineas.
[in]YVector resultados $\mathbf{y}$.
[in]W0Primeiro valor de $\mathbf{w}$.
Devuelve
Unvector de pesos.
Ejemplos
example_logisticregression_ce_svm_hard.cpp y example_logisticregression_svm.cpp.

◆ FittingOrtogonalIG()

Pds::Vector Pds::LogisticModel::FittingOrtogonalIG ( const Pds::Matrix &  X,
const Pds::Vector &  Y,
unsigned int  MinID 
)

Calculo de pesos.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right)\equiv \left( \begin{matrix} \mathbf{v}_1& \mathbf{v}_2& \hdots& \mathbf{v}_N& \end{matrix} \right), \qquad \mathbf{y} = \left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right), \]

\[ \begin{array}{l} for(n=0;n<N;n++)\\ \{\\ \qquad \mathbf{y_s} \leftarrow \mathbf{y}\\ \qquad Sort~ascending~\mathbf{v}_n~and~rearrange~\mathbf{y_s};\\ \qquad \{ID_{n},IG_{n},Sign_{n}\}\leftarrow GetBestInformationGainID(\mathbf{y_s},0.5,MinID);\\ \qquad umbral_{n}\leftarrow \mathbf{v}_n[ID_{n}]\\ \}\\ ~\\ n_{opt}\leftarrow arg_n max~IG_{n}\\ ~\\ if(Sign_{n_{opt}}==0)\\ \qquad w_0 \leftarrow \mathbf{v}_{n_{opt}}[ID_{n_{opt}}] \\ \qquad w_{n_{opt}} \leftarrow -1 \\ else\\ \qquad w_0 \leftarrow -\mathbf{v}_{n_{opt}}[ID_{n_{opt}}] \\ \qquad w_{n_{opt}} \leftarrow 1 \\ ~\\ \mathbf{w} \leftarrow (w_0,~w_1,~w_2,~...,w_N); \\ return ~\mathbf{w}; \end{array} \]

Parámetros
[in]XVector de datos $\mathbf{X}$.
[in]YVector de datos $\mathbf{y}$.
[in]MinIDCantidad minima de muestras en cada grupo separado. if(Y.Nel()<(2*MinID)) return Pds::Vector();
Devuelve
Un vector de pesos $\mathbf{w}$ si el cálculo es posible o una vacio si no.
Ejemplos
example_logisticregression_ig.cpp y example_logisticregression_ig2.cpp.

◆ FittingGradientIG()

Pds::Vector Pds::LogisticModel::FittingGradientIG ( Pds::IterationConf &  Conf,
const Pds::Matrix &  X,
const Pds::Vector &  Y,
const Pds::Vector &  W0 
)

Calculo de pesos.

\[ \mathbf{X}= \left( \begin{matrix} \mathbf{x}_1^{T}\\ \mathbf{x}_2^{T}\\ \vdots\\ \mathbf{x}_L^{T}\\ \end{matrix} \right), \qquad \mathbf{y} =\left(\begin{matrix} y_1\\ y_2\\ \vdots\\ y_L\\ \end{matrix}\right), \qquad \mathbf{w} =\left(\begin{matrix} w_0\\ w_1\\ \vdots\\ w_N\\ \end{matrix}\right) \]

\[ C(\mathbf{w})\equiv Pds::LogisticModel::CostInformationGain(\mathbf{w},\mathbf{X},\mathbf{y}) \]

\[ \frac{\partial C(\mathbf{w})}{\partial \mathbf{w}} \equiv Pds::LogisticModel::GradientCostInformationGain(\mathbf{w},\mathbf{X},\mathbf{y},h) \]

\[ E(\mathbf{w})\equiv -C(\mathbf{w}) \qquad \rightarrow \qquad \frac{\partial E(\mathbf{w})}{\partial \mathbf{w}}\equiv -\frac{\partial C(\mathbf{w})}{\partial \mathbf{w}} \]

\[ Repetir: \quad \mathbf{w} \leftarrow \mathbf{w} + \alpha \frac{\partial C(\mathbf{w})}{\partial \mathbf{w}} \]

Parámetros
[in]ConfObjeto de configuracion de iteraciones.
[in]XMatriz con los vectores de datos (muestras) en las lineas.
[in]YVector de datos de salida.
[in]W0Vector inicial de pesos.
Devuelve
Un vector de pesos $\mathbf{w}$ si el cálculo es posible o una vacio si no.
Ejemplos
example_logisticregression_ig.cpp y example_logisticregression_ig2.cpp.

◆ FittingParrallelPlaneIS()

Pds::Vector Pds::LogisticModel::FittingParrallelPlaneIS ( const Pds::Matrix &  X,
const Pds::Vector &  Y,
const Pds::Vector &  W0,
double *  ISmin = NULL,
double  Delta = 0.001 
)

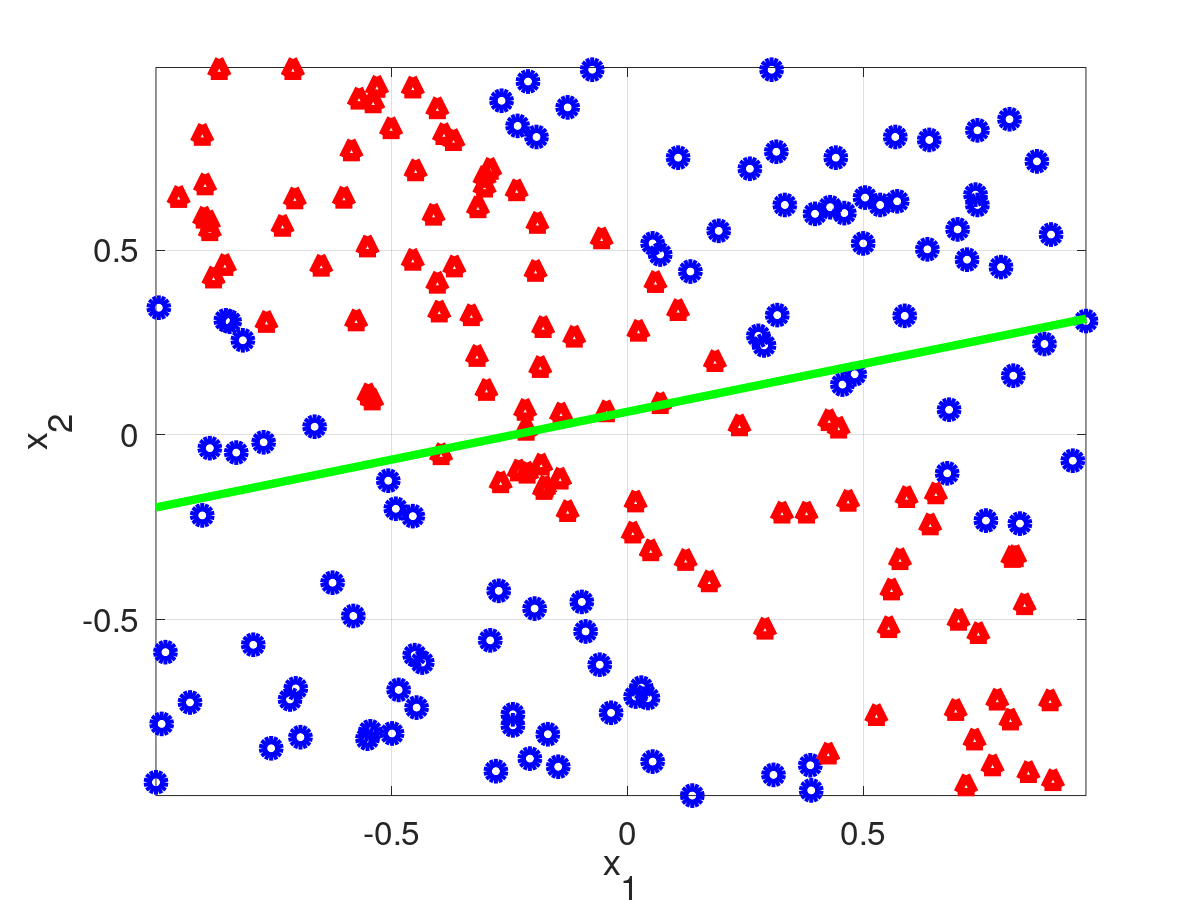
Calculo de pesos buscando el plano paralelo a W0 que genere la menor suma de informaciones en la particion, es equivalente a buscar la mayor information gain.

original
paralelo
Parámetros
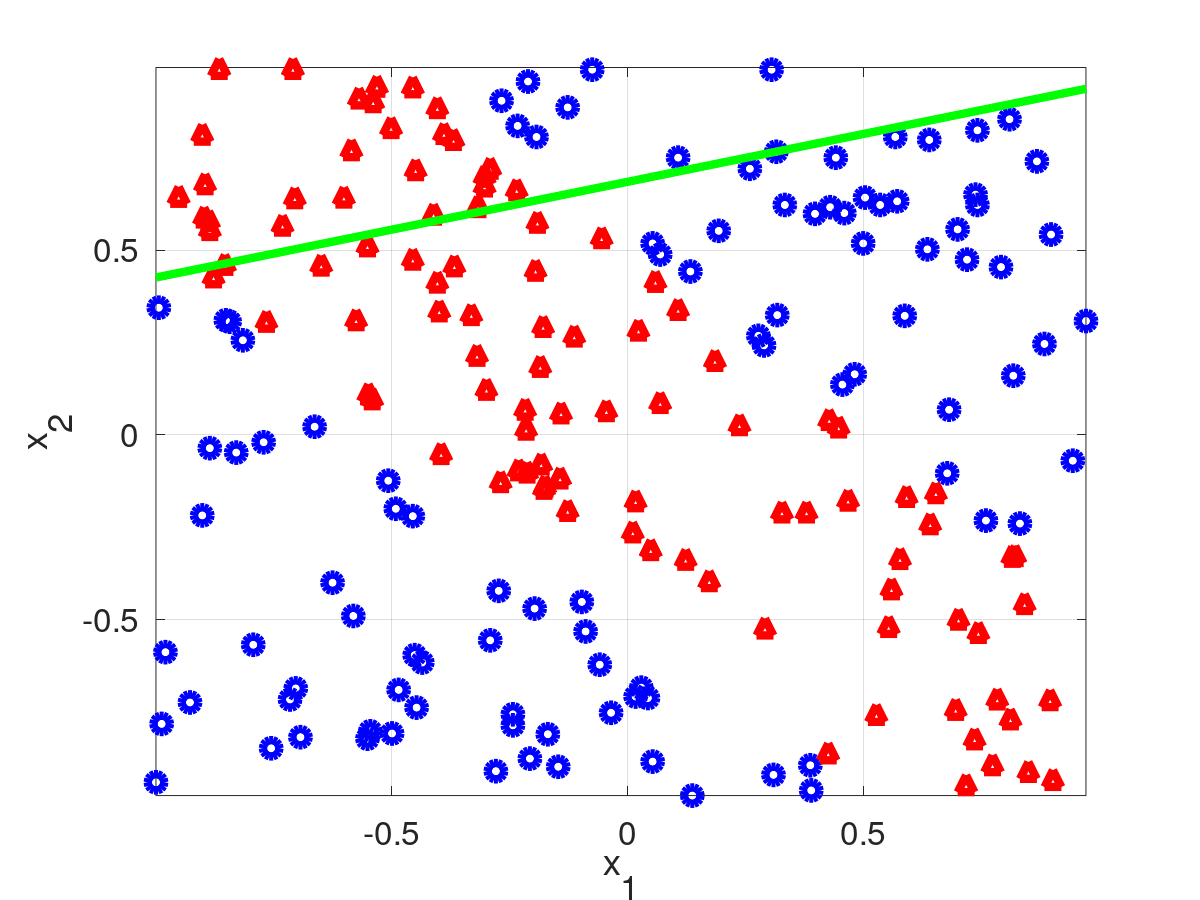
[in]XMatriz con los vectores de datos (muestras) en las lineas.
[in]YVector de datos de salida.
[in]W0Vector inicial de pesos.
[out]ISmin[Optional] Valor de la Information Sum mínima.
[in]DeltaFactor de ajuste.
Devuelve
Un vector de pesos $\mathbf{w}$ si el cálculo es posible o una vacio si no.
Ejemplos
example_logisticregression_paris.cpp.

◆ FittingByFactor()

Pds::Vector Pds::LogisticModel::FittingByFactor ( const Pds::Matrix &  X,
const Pds::Vector &  Y,
const Pds::Vector &  W0,
double  Delta = 0.001 
)

Aplica la teoria de Logit MeanSquare para ajustar W0 por um factor real adecuado.

Parámetros
[in]XMatriz con los vectores de datos (muestras) en las lineas.
[in]YVector de datos de salida.
[in]W0Vector inicial de pesos.
[in]DeltaFactor de ajuste.
Devuelve
Un vector de pesos $\mathbf{w}$ si el cálculo es posible o una vacio si no.

◆ LearningCurves()

Pds::DataErrorCurve Pds::LogisticModel::LearningCurves ( Pds::IterationConf &  Conf,
const Pds::Matrix &  Xtr,
const Pds::Vector &  Ytr,
const Pds::Matrix &  Xcv,
const Pds::Vector &  Ycv,
double  percent 
)

Retorna learning curve.

\[ \mathbf{R} \leftarrow [\mathbf{1}\quad \mathbf{X}]\]

\[ h_{\mathbf{w}}(\mathbf{X}) \leftarrow Sigmoid(\mathbf{R} \mathbf{w})\]

Parámetros
[in,out]ConfValores de configuracion de la iteracion.
[in]XtrDatos X de entrenamiento.
[in]YtrDatos Y de entrenamiento.
[in]XcvDatos X de cross-validation.
[in]YcvDatos Y de cross-validation.
[in]percentPorcentaje de datos testados.
Devuelve
Retorna una estructuras con las curvas de aprendisaje. Si Pds::DataErrorCurve Dat, entonces
  • Dat.Var[i] : Numero de muestras m usadas
  • Dat.ErrorTr[i] : CostCrossEntropy() de los datos de entrenamiento para un número de muestas m;
  • Dat.ErrorCv[i] : CostCrossEntropy() de los datos de cross-validation para un número de muestas m;

Enlaces de interés

HomePage Bazaar Download Bug report Ayuda Developer Feed
Manual de referencia generado el Domingo, 28 de Noviembre de 2021 13:03:56 para la biblioteca libpdsmlmm usando  Generado el Domingo, 28 de Noviembre de 2021 13:03:56 para libpdsmlmm por   doxygen 1.9.2