Clase que implementa una elipse en 2D. Más...

Namespaces
namespace	Pds
	Nombre de espacio para Pds (Procesamiento Digital de Senales)

Estructuras de datos
class	Pds::Ellipse
	La clase tipo Pds::Ellipse . Esta clase genera un objeto con dos parámetros xc1, xc2 y a. Para usar incluir Pds/Ellipse. Más...

Varios tipos de constructores
Crean una objeto Pds::Ellipse
	Pds::Ellipse::Ellipse (void)
	Crea un objeto vacio de tipo Pds::Ellipse. Más...

	Pds::Ellipse::Ellipse (double a, double b, double xo1, double xo2, double angle)
	Crea un objeto de tipo Pds::Ellipse. Más...

	Pds::Ellipse::Ellipse (const Pds::Vector &xc1, const Pds::Vector &xc2, double a)
	Crea un objeto de tipo Pds::Ellipse. Más...

	Pds::Ellipse::Ellipse (const Pds::Point2D &xc1, const Pds::Point2D &xc2, double a)
	Crea un objeto de tipo Pds::Ellipse. Más...

	Pds::Ellipse::Ellipse (double A, double B, double C, double D, double E, double F)
	Crea un objeto de tipo Pds::Ellipse. Más...

	Pds::Ellipse::Ellipse (const Pds::Ellipse &B)
	Crea un objeto de tipo Pds::Ellipse copiando datos desde otro. Más...

	Pds::Ellipse::~Ellipse ()

Get samples
Pds::Matrix	Pds::Ellipse::RandPerimeter (unsigned int L) const
	Retorna, en las lineas de la matriz, muestras que describen el perímetro del elipse. Más...

Pds::Matrix	Pds::Ellipse::RandSamples (unsigned int L) const
	Retorna, en las lineas de la matriz, muestras que describen el elipse interno. Más...

Eval samples
Pds::Vector	Pds::Ellipse::EvalSamples (const Pds::Matrix &X) const
	Evalua cada linea $\mathbf{x}^{(l)}$ de la matrix $\mathbf{X}$ en la ecuación $f(\mathbf{x}^{(l)})$ . Más...

double	Pds::Ellipse::Evaluate (double x1, double x2) const
	Evalua un punto en la elipse. Más...

double	Pds::Ellipse::Evaluate (const Pds::Point2D &p) const
	Evalua un punto en la elipse. Más...

Get data
Pds::Vector	Pds::Ellipse::GetMajorVector (void) const
	Retorna $\mathbf{\bar{a}}$ el vector del eje mayor. Más...

Pds::Vector	Pds::Ellipse::GetMinorVector (void) const
	Retorna $\mathbf{\bar{b}}$ el vector del eje menor. Más...

double	Pds::Ellipse::GetMajorAxis (void) const
	Retorna la distancia del eje mayor. Más...

double	Pds::Ellipse::GetMinorAxis (void) const
	Retorna la distancia del eje menor. Más...

double	Pds::Ellipse::GetAngle (void) const
	Retorna el angulo del eje mayor. Más...

Pds::Vector	Pds::Ellipse::GetCentroid (void) const
	Retorna el centro de la elipse. Más...

Pds::Vector	Pds::Ellipse::GetCentroid1 (void) const
	Retorna $\mathbf{x}_{c1}$ el centroide 1 de la elipse. Más...

Pds::Vector	Pds::Ellipse::GetCentroid2 (void) const
	Retorna $\mathbf{x}_{c2}$ el centroide 2 de la elipse. Más...

double	Pds::Ellipse::GetArea (void) const
	Retorna el area $a b \pi$ de la elipse. Más...

bool	Pds::Ellipse::GetQuadraticForm (double &A, double &B, double &C, double &D, double &E, double &F) const
	Retorna los parámetros de la forma cuadrática. Más...

Static variados Pds::Ellipse
static Pds::Ellipse	Pds::Ellipse::GetEllipse (const Pds::Matrix &X, const std::string &Type="CovEig")
	Aproxima uma elipse a partir de muestras $\mathbf{x}_{l}$ agrupadas en las lineas de la matriz $\mathbf{X}$ . Más...

static Pds::Ellipse	Pds::Ellipse::GetEllipseCovEigMethod (const Pds::Matrix &X)
	Aproxima uma elipse a partir de muestras $\mathbf{x}_{l}$ agrupadas en las lineas de la matriz $\mathbf{X}$ . Más...

Memory Pds::Ellipse
Pds::Ellipse &	Pds::Ellipse::operator= (const Pds::Ellipse &B)
	Copia en si mismo (A), un Shape B. Este operador es similar al método Copy(). Más...

bool	Pds::Ellipse::Copy (const Pds::Ellipse &B)
	Copia en si mismo (A), el contenido de un Shape B. Este método es similar a usar el operador = . Más...

void	Pds::Ellipse::MakeEmpty (void)
	Cera los datos internos. Más...

State Pds::Ellipse
bool	Pds::Ellipse::IsEmpty (void) const
	Verifica si la elipse es válido. Más...

bool	Pds::Ellipse::IsInside (double x1, double x2) const
	Verifica si un elemento esta en la elipse o el perímetro. Más...

bool	Pds::Ellipse::IsInside (const Pds::Point2D &p) const
	Verifica si un elemento esta en la elipse o el perímetro. Más...

Mostrando datos
void	Pds::Ellipse::Print (std::string str="") const
	Muestra en pantalla el contenido de Pds::Ellipse, elementos separados por tabulador. Más...

Métodos para exportar e importar Json con Pds::Ellipse.
Herramientas genéricas que pueden ser usadas desde Pds::Ellipse
Pds::Json	Pds::Ellipse::ToJson (void) const
	Retorna un objeto Pds::Json con el contenido del objeto. Más...

bool	Pds::Ellipse::FromJson (const Pds::Json &J)
	Lee un objeto Pds::Json busca la etiqueta "Ellipse" y lo carga. El objeto debe tener al menos los siguientes dados. Más...

Operadores no miembros de Ellipse
Descripcion de algunos operadores habilitados a trabajar con Pds::Ellipse.
std::ostream &	operator<< (std::ostream &out, const Pds::Ellipse &z)
	Retorna el contenido del objeto por la salida estándar. Más...

Descripción detallada

Clase que implementa una elipse en 2D.

#include <Pds/Ellipse>

Documentación de las funciones

◆ Ellipse() [1/6]

Pds::Ellipse::Ellipse ( void )

Crea un objeto vacio de tipo Pds::Ellipse.

◆ Ellipse() [2/6]

Pds::Ellipse::Ellipse	(	double	a,
		double	b,
		double	xo1,
		double	xo2,
		double	angle
	)

Crea un objeto de tipo Pds::Ellipse.

La elipse se define por $\mathbf{x}_{c1}$ , $\mathbf{x}_{c2}$ y , donde:

$c\leftarrow\sqrt{a^2-b^2},$

$\mathbf{x}_{c1}\leftarrow\mathbf{x}_{o}+c~[cos(\theta)\quad sin(\theta)]^{T},$

$\mathbf{x}_{c2}\leftarrow\mathbf{x}_{o}-c~[cos(\theta)\quad sin(\theta)]^{T},$

$Ellipse= \{ \mathbf{x} \in \mathbb{R}^2~|~ \|\mathbf{x}-\mathbf{x}_{c1}\|+\|\mathbf{x}-\mathbf{x}_{c2}\|=2a \}$

Ellipse.png

Parámetros

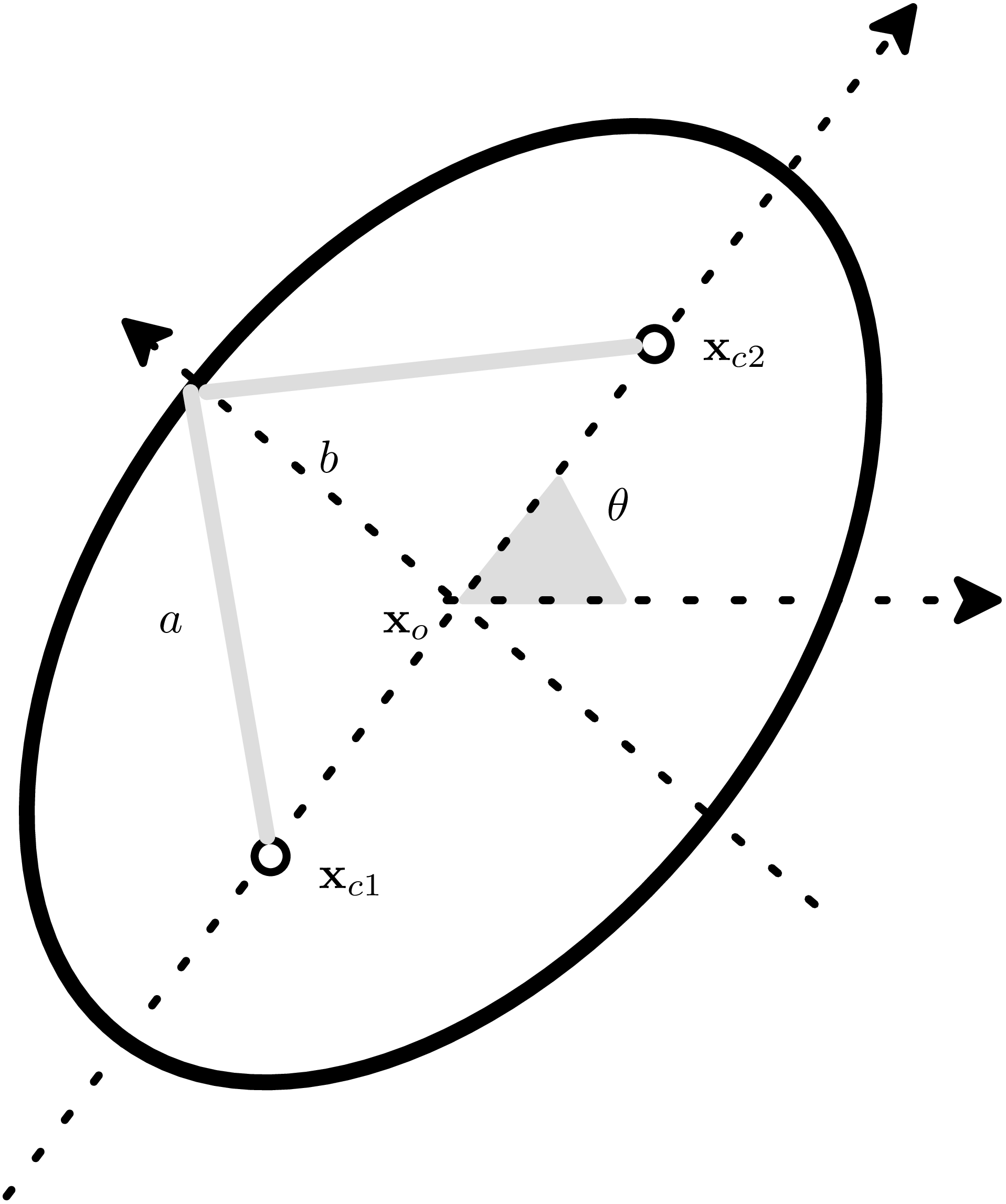
[in]	a	Major axis.
[in]	b	Minor axis.
[in]	xo1	Parámetro $x_{o1}$ do centroide $\mathbf{x}_{o}=(x_{o1},x_{o2})$ .
[in]	xo2	Parámetro $x_{o2}$ do centroide $\mathbf{x}_{o}=(x_{o1},x_{o2})$ .
[in]	angle	Angulo $\theta$ antihorario de rotacion de la elipse.

◆ Ellipse() [3/6]

Pds::Ellipse::Ellipse	(	const Pds::Vector &	xc1,
		const Pds::Vector &	xc2,
		double	a
	)

Crea un objeto de tipo Pds::Ellipse.

La elipse se define por $\mathbf{x}_{c1}$ , $\mathbf{x}_{c2}$ y , donde:

$Ellipse= \{ \mathbf{x} \in \mathbb{R}^2~|~ \|\mathbf{x}-\mathbf{x}_{c1}\|+\|\mathbf{x}-\mathbf{x}_{c2}\|=2a \quad and \quad \|\mathbf{x}_{c2}-\mathbf{x}_{c1}\| <2a \}$

Ellipse.png

Parámetros

[in]	xc1	Centroide $\mathbf{x}_{c1}$ .
[in]	xc2	Centroide $\mathbf{x}_{c2}$ .
[in]	a	Major axis.

◆ Ellipse() [4/6]

Pds::Ellipse::Ellipse	(	const Pds::Point2D &	xc1,
		const Pds::Point2D &	xc2,
		double	a
	)

Crea un objeto de tipo Pds::Ellipse.

La elipse se define por $\mathbf{x}_{c1}$ , $\mathbf{x}_{c2}$ y , donde:

$Ellipse= \{ \mathbf{x} \in \mathbb{R}^2~|~ \|\mathbf{x}-\mathbf{x}_{c1}\|+\|\mathbf{x}-\mathbf{x}_{c2}\|=2a \quad and \quad \|\mathbf{x}_{c2}-\mathbf{x}_{c1}\| <2a \}$

Ellipse.png

Parámetros

[in]	xc1	Centroide $\mathbf{x}_{c1}$ .
[in]	xc2	Centroide $\mathbf{x}_{c2}$ .
[in]	a	Major axis.

◆ Ellipse() [5/6]

Pds::Ellipse::Ellipse	(	double	A,
		double	B,
		double	C,
		double	D,
		double	E,
		double	F
	)

Crea un objeto de tipo Pds::Ellipse.

La elipse se define por $\mathbf{x}_{o}=(x_{o1},x_{o2})$ , , y $\theta$ , entonces:

$\begin{array}{ll} a,b&={\frac {-{\sqrt {2{\Big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{\Big )}\left((A+C)\pm {\sqrt {(A-C)^{2}+B^{2}}}\right)}}}{B^{2}-4AC}}\\ x_{o1 }&={\frac {2CD-BE}{B^{2}-4AC}}\\[3pt] x_{o2 }&={\frac {2AE-BD}{B^{2}-4AC}}\\[3pt] \theta &={\begin{cases}\arctan \left({\frac {1}{B}}\left(C-A-{\sqrt {(A-C)^{2}+B^{2}}}\right)\right)&{\text{for }}B\neq 0\\0&{\text{for }}B=0,\ A<C\\90^{\circ }&{\text{for }}B=0,\ A>C\\\end{cases}} \end{array}$

$f(\mathbf{x})\equiv f(x_{1},x_{1})\equiv Ax_{1}^{2}+Bx_{1}x_{2}+Cx_{2}^{2}+Dx_{1}+Ex_{2}+F=0$

Ellipse.png

Parámetros

[in]	A	Parámetro A.
[in]	B	Parámetro B.
[in]	C	Parámetro C.
[in]	D	Parámetro D.
[in]	E	Parámetro E.
[in]	F	Parámetro F.

◆ Ellipse() [6/6]

Pds::Ellipse::Ellipse ( const Pds::Ellipse & B )

Crea un objeto de tipo Pds::Ellipse copiando datos desde otro.

Parámetros

[in] B Ellipse a copiar.

◆ RandPerimeter()

Pds::Matrix Pds::Ellipse::RandPerimeter ( unsigned int L ) const

Retorna, en las lineas de la matriz, muestras que describen el perímetro del elipse.

Sea $\alpha\sim U(0,2\pi)$ una variable aleatoria uniformente distribuida entre y $2\pi$ , $\mathbf{\bar{a}}$ el vector mayor, $\mathbf{\bar{b}}$ el vector menor y $\mathbf{x}_{o}$ el centroide de la elipse, entonces un punto aleatorio $\mathbf{p}$ del perímetro es definido como:

$\mathbf{p}=\mathbf{x}_{o}+ \mathbf{\bar{a}}~cos(\alpha)+ \mathbf{\bar{b}}~sin(\alpha)$

example_ellipse_create_randperimeter.png

Parámetros

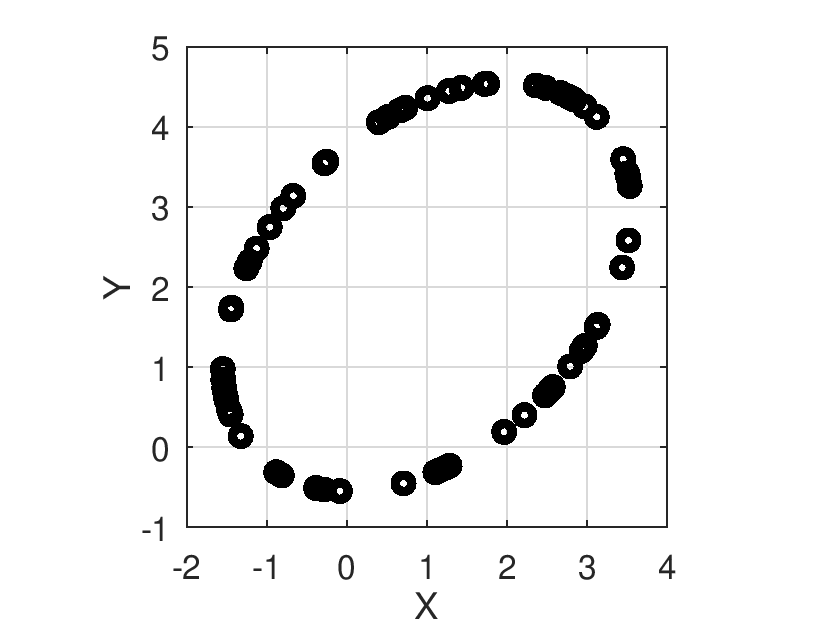
[in] L Número de muestras

Devuelve: Retorna, en las lineas de la matriz, muestras que describen el perímetro del elipse, o una matriz vacia en caso de error.

Ejemplos: example_ellipse_create.cpp y example_ellipse_getellipse.cpp.

◆ RandSamples()

Pds::Matrix Pds::Ellipse::RandSamples ( unsigned int L ) const

Retorna, en las lineas de la matriz, muestras que describen el elipse interno.

$\begin{array}{l} \mathbf{for}~l=1:L\\ \qquad\mathbf{do:}\\ \qquad\qquad (x_1,x_2)\leftarrow random(...);\\ \qquad\mathbf{while}((Ax_{1}^{2}+Bx_{1}x_{2}+Cx_{2}^{2}+Dx_{1}+Ex_{2}+F)>0);\\ \qquad add~(x_1,x_2)~to~\mathbf{P}\\ \mathbf{return}~\mathbf{P}\\ \end{array}$

example_ellipse_create_randsamples.png

Parámetros

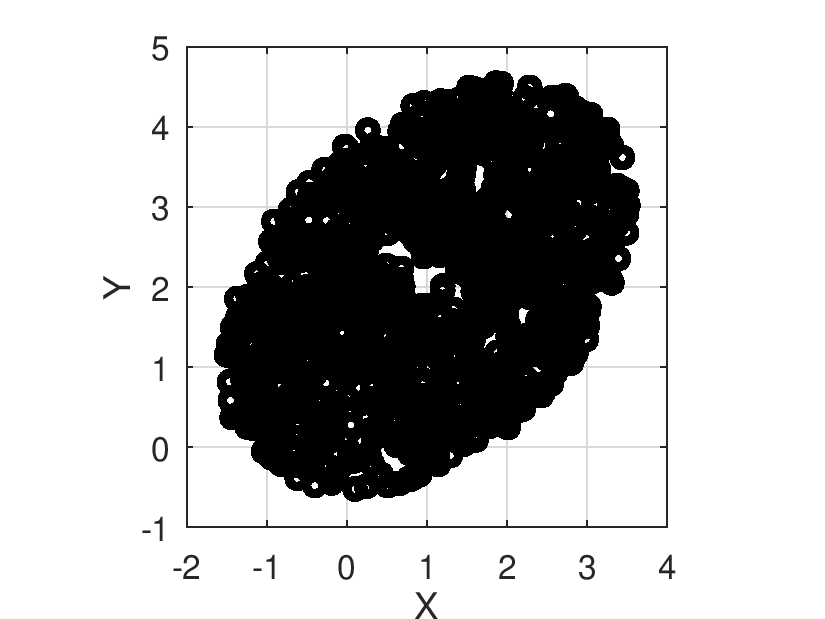
[in] L Número de muestras

Devuelve: Retorna, en las lineas de la matriz, muestras que describen el elipse interno, o una matriz vacia en caso de error.

Ejemplos: example_ellipse_create.cpp y example_ellipse_getellipse.cpp.

◆ EvalSamples()

Pds::Vector Pds::Ellipse::EvalSamples ( const Pds::Matrix & X ) const

Evalua cada linea $\mathbf{x}^{(l)}$ de la matrix $\mathbf{X}$ en la ecuación $f(\mathbf{x}^{(l)})$ .

$f(\mathbf{x})\equiv f(x_{1},x_{1})\equiv Ax_{1}^{2}+Bx_{1}x_{2}+Cx_{2}^{2}+Dx_{1}+Ex_{2}+F$

Parámetros

[in] X Matriz $\mathbf{X}$ de muestras.

Devuelve: Retorna un vector con la función $f(\mathbf{x}^{(l)})$ evaluada en cada muestra $\mathbf{x}^{(l)}$ de la matrix $\mathbf{X}$ .

◆ Evaluate() [1/2]

double Pds::Ellipse::Evaluate	(	double	x1,
		double	x2
	)		const

Evalua un punto en la elipse.

calcula la forma cuadrática GetQuadraticForm() y verifica si:

$f(\mathbf{x})\equiv f(x_{1},x_{1})\equiv Ax_{1}^{2}+Bx_{1}x_{2}+Cx_{2}^{2}+Dx_{1}+Ex_{2}+F$

Atención: Posibles errores de redondeo en el borde.

Parámetros

[in]	x1	Primera variable de p=(x1,x2).
[in]	x2	Segunda variable de p=(x1,x2).

Devuelve: Retorna true si está dentro de la elipse o el perímetro, o false si no.

Ejemplos: example_ellipse_state.cpp.

◆ Evaluate() [2/2]

double Pds::Ellipse::Evaluate ( const Pds::Point2D & p ) const

Evalua un punto en la elipse.

calcula la forma cuadrática GetQuadraticForm() y verifica si:

$f(\mathbf{x})\equiv f(x_{1},x_{1})\equiv Ax_{1}^{2}+Bx_{1}x_{2}+Cx_{2}^{2}+Dx_{1}+Ex_{2}+F$

Atención: Posibles errores de redondeo en el borde.

Parámetros

[in] p Variable p=(x1,x2).

Devuelve: Retorna true si está dentro de la elipse o el perímetro, o false si no.

◆ GetMajorVector()

Pds::Vector Pds::Ellipse::GetMajorVector ( void ) const

Retorna $\mathbf{\bar{a}}$ el vector del eje mayor.

$\mathbf{\bar{a}} \leftarrow a \frac{\mathbf{x}_{c1}-\mathbf{x}_{c2}}{\|\mathbf{x}_{c1}-\mathbf{x}_{c2}\|}$

Devuelve: Retorna $\mathbf{\bar{a}}$ el vector del eje mayor, o un vector vacio en caso de error.

Ejemplos: example_ellipse_create.cpp.

◆ GetMinorVector()

Pds::Vector Pds::Ellipse::GetMinorVector ( void ) const

Retorna $\mathbf{\bar{b}}$ el vector del eje menor.

$\mathbf{d} \leftarrow \mathbf{x}_{c1}-\mathbf{x}_{c2}$

$b \leftarrow \sqrt{a^2-\frac{\|\mathbf{d}\|^2}{4}}$

$\mathbf{\bar{b}} \leftarrow b \frac{\mathbf{d}^{\bot}}{\|\mathbf{d}\|}$

Devuelve: Retorna $\mathbf{\bar{b}}$ el vector del eje menor, o un vector vacio en caso de error.

Ejemplos: example_ellipse_create.cpp.

◆ GetMajorAxis()

double Pds::Ellipse::GetMajorAxis ( void ) const

Retorna la distancia del eje mayor.

Devuelve: Retorna la distancia del eje mayor, o cero en caso de error.

Ejemplos: example_ellipse_create.cpp y example_ellipse_getellipse.cpp.

◆ GetMinorAxis()

double Pds::Ellipse::GetMinorAxis ( void ) const

Retorna la distancia del eje menor.

$\mathbf{d} \leftarrow \mathbf{x}_{c1}-\mathbf{x}_{c2}$

$b \leftarrow \sqrt{a^2-\frac{\|\mathbf{d}\|^2}{4}}$

Devuelve: Retorna la distancia del eje menor, o cero en caso de error.

Ejemplos: example_ellipse_create.cpp y example_ellipse_getellipse.cpp.

◆ GetAngle()

double Pds::Ellipse::GetAngle ( void ) const

Retorna el angulo del eje mayor.

$\mathbf{d} \leftarrow \mathbf{x}_{c1}-\mathbf{x}_{c2}$

$\theta \leftarrow angle(\mathbf{d})$

Devuelve: Retorna el angulo del eje mayor, o cero en caso de error.

Ejemplos: example_ellipse_create.cpp y example_ellipse_getellipse.cpp.

◆ GetCentroid()

Pds::Vector Pds::Ellipse::GetCentroid ( void ) const

Retorna el centro de la elipse.

$\mathbf{x}_{o}\leftarrow\frac{\mathbf{x}_{c1}+\mathbf{x}_{c2}}{2}$

Devuelve: Retorna el centro de la elipse, o un vector vacio en caso de error.

Ejemplos: example_ellipse_create.cpp y example_ellipse_getellipse.cpp.

◆ GetCentroid1()

Pds::Vector Pds::Ellipse::GetCentroid1 ( void ) const

Retorna $\mathbf{x}_{c1}$ el centroide 1 de la elipse.

Devuelve: Retorna $\mathbf{x}_{c1}$ el centroide 1 de la elipse, o un vector vacio en caso de error.

Ejemplos: example_ellipse_create.cpp.

◆ GetCentroid2()

Pds::Vector Pds::Ellipse::GetCentroid2 ( void ) const

Retorna $\mathbf{x}_{c2}$ el centroide 2 de la elipse.

Devuelve: Retorna $\mathbf{x}_{c2}$ el centroide 2 de la elipse, o un vector vacio en caso de error.

Ejemplos: example_ellipse_create.cpp.

◆ GetArea()

double Pds::Ellipse::GetArea ( void ) const

Retorna el area $a b \pi$ de la elipse.

Devuelve: Retorna el area $a b \pi$ de la elipse, o en caso de error.

◆ GetQuadraticForm()

bool Pds::Ellipse::GetQuadraticForm	(	double &	A,
		double &	B,
		double &	C,
		double &	D,
		double &	E,
		double &	F
	)		const

Retorna los parámetros de la forma cuadrática.

$Ax_{1}^{2}+Bx_{1}x_{2}+Cx_{2}^{2}+Dx_{1}+Ex_{2}+F=0$

$\begin{array}{ll} A&=a^{2}\sin ^{2}\theta +b^{2}\cos ^{2}\theta \\ B&=2\left(b^{2}-a^{2}\right)\sin \theta \cos \theta \\ C&=a^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta \\ D&=-2Ax_{\circ }-By_{\circ }\\ E&=-Bx_{\circ }-2Cy_{\circ }\\ F&=Ax_{\circ }^{2}+Bx_{\circ }y_{\circ }+Cy_{\circ }^{2}-a^{2}b^{2}. \end{array}$

Parámetros

[out]	A	Parámetro A.
[out]	B	Parámetro B.
[out]	C	Parámetro C.
[out]	D	Parámetro D.
[out]	E	Parámetro E.
[out]	F	Parámetro F.

Devuelve: Retorna true si la elipse existe y false si no.

Ejemplos: example_ellipse_create.cpp.

◆ GetEllipse()

static Pds::Ellipse Pds::Ellipse::GetEllipse	(	const Pds::Matrix &	X,
		const std::string &	Type = `"CovEig"`
	)

static

Aproxima uma elipse a partir de muestras $\mathbf{x}_{l}$ agrupadas en las lineas de la matriz $\mathbf{X}$ .

Parámetros

[in]	X	Muestras $\mathbf{x}_{l}$
[in]	Type	Tipo de cálculo. CovEig: usa GetEllipseCovEigMethod(); agrupadas en las lineas de la matriz $\mathbf{X}$ .

Ejemplos: example_ellipse_getellipse.cpp.

◆ GetEllipseCovEigMethod()

static Pds::Ellipse Pds::Ellipse::GetEllipseCovEigMethod ( const Pds::Matrix & X )

static

Aproxima uma elipse a partir de muestras $\mathbf{x}_{l}$ agrupadas en las lineas de la matriz $\mathbf{X}$ .

$\mathbf{X} \equiv \left[ \begin{matrix} \mathbf{x}_{0}\\ \mathbf{x}_{1}\\ \vdots\\ \mathbf{x}_{L-1} \end{matrix} \right]$

$\boldsymbol{\mu}_{\mathbf{x}} \leftarrow \left[ \begin{matrix} \mu_{\mathbf{c}_{0}} ~~ \mu_{\mathbf{c}_{1}} \end{matrix} \right] \equiv \frac{1}{L}\sum_{l}^{L} \mathbf{x}_{l}$

$\mathbf{S}\equiv \frac{1}{L-1}\sum_{l}^{L} (\mathbf{x}_{l}-\boldsymbol{\mu}_{\mathbf{x}})^{T}(\mathbf{x}_{l}-\boldsymbol{\mu}_{\mathbf{x}})$

Calculando Eigenvalues y Eigenvector:

$\{\boldsymbol{\lambda},~ \mathbf{V}\}\leftarrow eig\left(\mathbf{S}\right)$

Con los eigenvalues en orden ascendente

$\boldsymbol{\lambda}=\left[\lambda_0,~\lambda_1\right],\qquad \mathbf{V}=\left[\mathbf{v}_0,~\mathbf{v}_1\right]$

definimos a elipse

$a=\sqrt{\lambda_1}, \quad b=\sqrt{\lambda_0}, \quad \mathbf{x}_{o}= \left[ \mu_{\mathbf{c}_{0}},~ \mu_{\mathbf{c}_{1}} \right] \quad \theta = atan\left(\mathbf{v}_1\right)$

Calculamos a función $f(\mathbf{x}_{l})$ con la forma cuadrática de la elipse:

$f(\mathbf{x})=Ax_{1}^{2}+Bx_{1}x_{2}+Cx_{2}^{2}+Dx_{1}+Ex_{2}+F$

Calculamos

$\hat{l}=\underset{l}{arg\,max} \left\{f(\mathbf{x}_{l})\right\}$

Luego afirmamos que la elipse que envuelve a los puntos es la que posee la ecuación cuadrática $g(\mathbf{x})$ :

$g(\mathbf{x})=Ax_{1}^{2}+Bx_{1}x_{2}+Cx_{2}^{2}+Dx_{1}+Ex_{2}+F-f(\mathbf{x}_{\hat{l}})$

Parámetros

[in] X Muestras $\mathbf{x}_{l}$ agrupadas en las lineas de la matriz $\mathbf{X}$ .

◆ operator=()

Pds::Ellipse & Pds::Ellipse::operator= ( const Pds::Ellipse & B )

Copia en si mismo (A), un Shape B. Este operador es similar al método Copy().

$A \leftarrow B$

Cuando acontece:

Pds::Ellipse B(,1,2);

A=B;

Pds::Ellipse

La clase tipo Pds::Ellipse . Esta clase genera un objeto con dos parámetros xc1, xc2 y a....

Definition: Ellipse.hpp:57

Cuando NO acontece:

Pds::Ellipse A=Pds::Ellipse(1,2);

Parámetros

[in] B El Shape a copiar

Devuelve: Retorna el operador de la izquierda (acumulador) con el resultado, o un SHape vacío (this->IsEmpty() igual a true) en caso de error.

Ver también: Copy

◆ Copy()

bool Pds::Ellipse::Copy ( const Pds::Ellipse & B )

Copia en si mismo (A), el contenido de un Shape B. Este método es similar a usar el operador = .

$A \leftarrow B$

Parámetros

[in] B El Shape a copiar

Devuelve: Retorna true si todo fue bien o false si no. Si se retorna false el receptor no altera su contenido.

Ver también: Copy

◆ MakeEmpty()

void Pds::Ellipse::MakeEmpty ( void )

Cera los datos internos.

.

◆ IsEmpty()

bool Pds::Ellipse::IsEmpty ( void ) const

Verifica si la elipse es válido.

◆ IsInside() [1/2]

bool Pds::Ellipse::IsInside	(	double	x1,
		double	x2
	)		const

Verifica si un elemento esta en la elipse o el perímetro.

calcula la forma cuadrática GetQuadraticForm() y verifica si:

$Ax_{1}^{2}+Bx_{1}x_{2}+Cx_{2}^{2}+Dx_{1}+Ex_{2}+F\leq 0$

Atención: Posibles errores de redondeo en el borde.

Parámetros

[in]	x1	Primera variable de p=(x1,x2).
[in]	x2	Segunda variable de p=(x1,x2).

Devuelve: Retorna true si está dentro de la elipse o el perímetro, o false si no.

Ejemplos: example_ellipse_state.cpp.

◆ IsInside() [2/2]

bool Pds::Ellipse::IsInside ( const Pds::Point2D & p ) const

Verifica si un elemento esta en la elipse o el perímetro.

calcula la forma cuadrática GetQuadraticForm() y verifica si:

$Ax_{1}^{2}+Bx_{1}x_{2}+Cx_{2}^{2}+Dx_{1}+Ex_{2}+F\leq 0$

Atención: Posibles errores de redondeo en el borde.

Parámetros

[in] p Variable p=(x1,x2).

Devuelve: Retorna true si está dentro de la elipse o el perímetro, o false si no.

◆ Print()

void Pds::Ellipse::Print ( std::string str = "" ) const

Muestra en pantalla el contenido de Pds::Ellipse, elementos separados por tabulador.

Parámetros

[in] str Texto a mostrar antes de imprimir el contenido.

Ejemplos: example_ellipse_create.cpp y example_ellipse_export_json.cpp.

◆ ToJson()

Pds::Json Pds::Ellipse::ToJson ( void ) const

Retorna un objeto Pds::Json con el contenido del objeto.

Por exemplo:

{
     "Ellipse":
     {
             "xc1":[1,1],
             "xc2":[1.5,2.5],
             "r":2
     }
}

Devuelve: Retorna un objeto Pds::Json con el contenido del objeto.

Ejemplos: example_ellipse_export_json.cpp.

◆ FromJson()

bool Pds::Ellipse::FromJson ( const Pds::Json & J )

Lee un objeto Pds::Json busca la etiqueta "Ellipse" y lo carga. El objeto debe tener al menos los siguientes dados.

{
     "Ellipse":
     {
             "xc1":[1,1],
             "xc2":[1.5,2.5],
             "r":2
     }
}

Devuelve: Retorna true si la lectura sucedió sin errores y false si no. Si la lectura es incorrecta se vuelve vacia.

Ejemplos: example_ellipse_export_json.cpp.

◆ operator<<()

std::ostream & operator<<	(	std::ostream &	out,
		const Pds::Ellipse &	z
	)

Retorna el contenido del objeto por la salida estándar.

std::cout<<z;

Parámetros

[in]	out	La salida
[in]	z	La matriz a mostrar

Devuelve: Retorna la misma salida estándar out.

◆ ~Ellipse()

Pds::Ellipse::~Ellipse ( )

Namespaces

Estructuras de datos

Varios tipos de constructores

Get samples

Eval samples

Get data

Static variados Pds::Ellipse

Memory Pds::Ellipse

State Pds::Ellipse

Mostrando datos

Métodos para exportar e importar Json con Pds::Ellipse.

Operadores no miembros de Ellipse

Descripción detallada

Documentación de las funciones

◆ Ellipse() [1/6]

◆ Ellipse() [2/6]

◆ Ellipse() [3/6]

◆ Ellipse() [4/6]

◆ Ellipse() [5/6]

◆ Ellipse() [6/6]

◆ RandPerimeter()

◆ RandSamples()

◆ EvalSamples()

◆ Evaluate() [1/2]

◆ Evaluate() [2/2]

◆ GetMajorVector()

◆ GetMinorVector()

◆ GetMajorAxis()

◆ GetMinorAxis()

◆ GetAngle()

◆ GetCentroid()

◆ GetCentroid1()

◆ GetCentroid2()

◆ GetArea()

◆ GetQuadraticForm()

◆ GetEllipse()

◆ GetEllipseCovEigMethod()

◆ operator=()

◆ Copy()

◆ MakeEmpty()

◆ IsEmpty()

◆ IsInside() [1/2]

◆ IsInside() [2/2]

◆ Print()

◆ ToJson()

◆ FromJson()

◆ operator<<()

◆ ~Ellipse()

Enlaces de interés