Funciones que usan Pds::Ceo, Ejemplo: Pds::Ceo::Fusion::NaiveBayes(), etc. Más...

Namespaces
namespace	Pds
	Nombre de espacion para PDS (Procesamiento Digital de Senales)

Funciones para Joint Channel Decoding
Herramientas genéricas que pueden ser usadas en Joint Channel Decoding
Pds::Vector	Pds::Ceo::Binary::Fusion::NaiveBayes (double ps, Pds::Vector p, const Pds::Matrix &U, double Umbral=0.5)
	Retorna una aproximación $\mathbf{\hat{u}}_s$ del vector $\mathbf{u}_s$ a partir de las muestras en $\mathbf{U}$ . Más...

Funciones para el calculo del BER en Symetric Binary Ceo Problem.
Herramientas genéricas para calcular la Bit Error Rate.
double	Pds::Ceo::Binary::Ber::SymetricModel (double rho, unsigned int M)
	Retorna la taza de erro de bit, , en el problema CEO binario simétrico de M fontes $u_m, \forall ~ m \in \{1, 2, ..., M\}$ , donde $\hat{u}_s$ representa la mejor aproximación de conociendo . Más...

Pds::Vector	Pds::Ceo::Binary::Ber::SymetricModel (const Pds::Vector &Rho, unsigned int M)
	Retorna la taza de erro de bit, , en el problema CEO binario simétrico de M fontes $u_m, \forall ~ m \in \{1, 2, ..., M\}$ , donde $\hat{u}_s$ representa la mejor aproximación de conociendo . Más...

Funciones para el calculo de probabilidades.
Herramientas genéricas para calcular probabilidades
double	Pds::Ceo::Binary::Probability::PjOmegaM (const Pds::Vector &OmegaM, const Pds::Vector &p, double ps, double Umbral=0.5)
	Encuentra la probabilidad conjunta $P(\Omega_M)$ de tener en la salida de un grupo de canales BSC un conjunto de valores binarios formando un vector $\Omega_M$ [7]. Más...

double	Pds::Ceo::Binary::Probability::PcUsOmegaM (const Pds::Vector &OmegaM, const Pds::Vector &p, bool us, double ps, double *PjU0OmegaM=NULL, double Umbral=0.5)
	Encuentra las probabilidades condicionada $P(u_s \|\Omega_M)$ y conjunta $P(u_s \Omega_M)$ [7] . Más...

Funciones para el calculo de la Joint Entropy.
Herramientas genéricas para calcular la entropia conjunta
double	Pds::Ceo::Binary::Entropy::HjOmegaM (const Pds::Vector &p, double ps=0.5)
	Encuentra la entropia conjunta $H(\Omega_M)\equiv H(u_1,...,u_M)$ para fontes generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s\| u_s)=p_m$ [7] . Más...

double	Pds::Ceo::Binary::Entropy::HjsOmegaM (double rho, unsigned int M, double ps=0.5)
	Encuentra la entropia conjunta $H(\Omega_M) \equiv h_{J}(\rho,M)$ para fontes generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s\| u_s)=p_m\equiv \rho$ [1]. Más...

double	Pds::Ceo::Binary::Entropy::HjsOmegaMInv (double HJoint, short int M, double ps=0.5)
	Encuentra el valor $\rho$ que genera la entropia conjunta $H(\Omega_M) \equiv h_{J}(\rho,M)$ para fontes generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s\| u_s)=p_m\equiv \rho$ [1] [2]. Más...

Funciones para el calculo de la Conditional Entropy.
Herramientas genéricas para calcular la entropia condicionada
double	Pds::Ceo::Binary::Entropy::HcUsOmegaM (const Pds::Vector &p, double ps)
	Encuentra la entropia condicionada. $H(u_s\|\Omega_M)$ [5]. Más...

double	Pds::Ceo::Binary::Entropy::HcsUsOmegaM (double rho, unsigned int M, double ps=0.5)
	Encuentra la entropia condicionada $H(u_s\|\Omega_M)\equiv h_{C}(\rho,M,p_s)$ [5] pp.37. Más...

Pds::Vector	Pds::Ceo::Binary::Entropy::HcsUsOmegaM (const Pds::Vector &Rho, unsigned int M, double ps=0.5)
	Encuentra la entropia condicionada $H(u_s\|\Omega_M)\equiv h_{C}(\rho,M,p_s)$ [5] pp.37. Más...

double	Pds::Ceo::Binary::Entropy::HcsUsOmegaMInv (double HCond, short int M, double ps=0.5)
	Encuentra la inversa $\rho$ de la entropia condicionada $H(u_s\|\Omega_M)\equiv h_{C}(\rho,M,p_s)$ para fontes generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s\| u_s)=p_m\equiv \rho$ [5] pp.37, [4]. Más...

Descripción detallada

Funciones que usan Pds::Ceo, Ejemplo: Pds::Ceo::Fusion::NaiveBayes(), etc.

#include <Pds/FuncCeoModel>

Binary CEO problem

Informacion adicional puede ser encontrada en [6]

Documentación de las funciones

◆ NaiveBayes()

Pds::Vector Pds::Ceo::Binary::Fusion::NaiveBayes	(	double	ps,
		Pds::Vector	p,
		const Pds::Matrix &	U,
		double	Umbral = `0.5`
	)

Retorna una aproximación $\mathbf{\hat{u}}_s$ del vector $\mathbf{u}_s$ a partir de las muestras en $\mathbf{U}$ .

$\mathbf{U}= \begin{bmatrix} \Omega_M^{(1)}\\ \Omega_M^{(2)}\\ \vdots\\ \Omega_M^{(L)} \end{bmatrix} \qquad \rightarrow \qquad \mathbf{\hat{u}}_s= \begin{bmatrix} \hat{u}^{(1)}\\ \hat{u}^{(2)}\\ \vdots\\ \hat{u}^{(L)} \end{bmatrix} \equiv Pds::Ceo::Fusion::NaiveBayes(ps,p,\mathbf{U})$

Parámetros

[in]	ps	Probabilidade .
[in]	p	Probabilidades de error de los BSC, $P(u_m \neq u_s \| u_s) \equiv p_m,~\forall~m\in\{1,...,M\}$
[in]	U	Matriz $\mathbf{U}$ a decodificar, con los datos de los canales en la lineas.
[in]	Umbral	Umbral de binarizacion de los datos en $\mathbf{U}$ , $\mathbf{U}\leftarrow\mathbf{U}\geq Umbral$ .

Devuelve: Retorna una aproximación $\mathbf{\hat{u}}_s$ del vector $\mathbf{u}_s$ a partir de las muestras en $\mathbf{U}$ .

Ejemplos: example_ceo_model.cpp, example_ceo_model_fusion.cpp y example_ceo_model_fusion2.cpp.

◆ SymetricModel() [1/2]

double Pds::Ceo::Binary::Ber::SymetricModel	(	double	rho,
		unsigned int	M
	)

Retorna la taza de erro de bit, , en el problema CEO binario simétrico de M fontes $u_m, \forall ~ m \in \{1, 2, ..., M\}$ , donde $\hat{u}_s$ representa la mejor aproximación de conociendo .

Estas fuentes son generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s | u_s) \equiv p_m\equiv \rho$ .

Quando M es impar :

$BER= \sum_{j=\frac{M+1}{2}}^{M} {{M}\choose{j}} {\rho}^j (1-\rho)^{M-j}$

Quando M es par :

$BER= 0.5 {{M}\choose{M/2}} {\rho}^{M/2} (1-\rho)^{M/2}+\sum_{j=\frac{M}{2}+1}^{M} {{M}\choose{j}} {\rho}^j (1-\rho)^{M-j}$

The formula for calculus of BER is in [3] and other simplification in [1] [2] .

Parámetros

[in]	rho	Es la probabilidad de error de los canales BSC. $P(u_m \neq u_s\| u_s)\equiv p_m\equiv \rho$ .
[in]	M	Es el número de canales BSC.

Devuelve: El valor .

Ejemplos: example_channel_model_bsc.cpp.

◆ SymetricModel() [2/2]

Pds::Vector Pds::Ceo::Binary::Ber::SymetricModel	(	const Pds::Vector &	Rho,
		unsigned int	M
	)

Retorna la taza de erro de bit, , en el problema CEO binario simétrico de M fontes $u_m, \forall ~ m \in \{1, 2, ..., M\}$ , donde $\hat{u}_s$ representa la mejor aproximación de conociendo .

Estas fuentes son generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s | u_s) \equiv p_m\equiv \rho$ .

Quando M es impar :

$BER= \sum_{j=\frac{M+1}{2}}^{M} {{M}\choose{j}} {\rho}^j (1-\rho)^{M-j}$

Quando M es par :

$BER= 0.5 {{M}\choose{M/2}} {\rho}^{M/2} (1-\rho)^{M/2}+\sum_{j=\frac{M}{2}+1}^{M} {{M}\choose{j}} {\rho}^j (1-\rho)^{M-j}$

The formula for calculus of BER is in [3] and other simplification in [1] [2] .

Parámetros

[in]	Rho	Un vector con las probabilidades de error de los canales BSC. $P(u_m \neq u_s\| u_s)\equiv p_m\equiv \rho$ .
[in]	M	Es el número de canales BSC.

Devuelve: Un vector de valores .

◆ PjOmegaM()

double Pds::Ceo::Binary::Probability::PjOmegaM	(	const Pds::Vector &	OmegaM,
		const Pds::Vector &	p,
		double	ps,
		double	Umbral = `0.5`
	)

Encuentra la probabilidad conjunta $P(\Omega_M)$ de tener en la salida de un grupo de canales BSC un conjunto de valores binarios formando un vector $\Omega_M$ [7].

Conocido un conjunto $\Omega_M=\{u_1, u_2, ..., u_M\}$ de fuentes binarias, estas son construidas pasando la fuente binaria con , por M canales BSC con probabilidad de error $P(u_m \neq u_s| u_s)=p_m$ .

Entonces este tendrá como probabilidad:

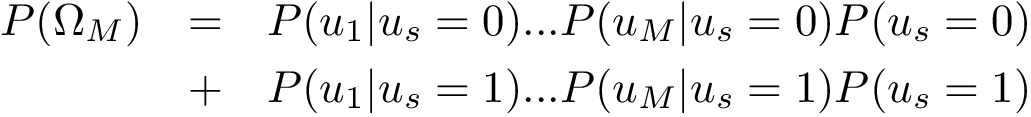
$\begin{eqnarray*} P(\Omega_M)& = & P(u_1|u_s=0) ... P(u_M|u_s=0) P(u_s=0) \\ ~ & + & P(u_1|u_s=1) ... P(u_M|u_s=1) P(u_s=1) \end{eqnarray*}$

Parámetros

[in]	OmegaM	$\Omega_M$ es un caso de ocurrencia del vector binario.
[in]	p	Probabilidades de error de los BSC, $P(u_m \neq u_s \| u_s) \equiv p_m,~\forall~m\in\{1,...,M\}$
[in]	ps	Probabilida de la fuente .
[in]	Umbral	Umbral para binarizar $\Omega_M$ . $\Omega_M\leftarrow \Omega_M\geq Umbral$ .

Devuelve: Retorna $P(\Omega_M)$ , la probabilidad conjuta del caso de ocurrencia de $\Omega_M$ .

◆ PcUsOmegaM()

double Pds::Ceo::Binary::Probability::PcUsOmegaM	(	const Pds::Vector &	OmegaM,
		const Pds::Vector &	p,
		bool	us,
		double	ps,
		double *	PjU0OmegaM = `NULL`,
		double	Umbral = `0.5`
	)

Encuentra las probabilidades condicionada $P(u_s |\Omega_M)$ y conjunta $P(u_s \Omega_M)$ [7] .

Conocido un conjunto $\Omega_M=\{u_1, u_2, ..., u_M\}$ de fuentes binarias, estas son construidas pasando la fuente binaria con , por M canales BSC con probabilidad de error $P(u_m \neq u_s| u_s)=p_m$ .

Entonces este tendrá como probabilidad:

$P(u_s|\Omega_M) = \frac{P(u_s\Omega_M) }{P(\Omega_M)}$

Sabiendo que:

$P(u_s\Omega_M) = P(u_1|u_s) ... P(u_M|u_s) P(u_s)$

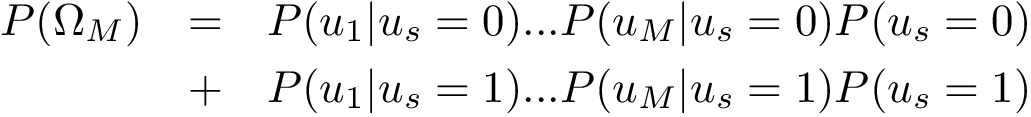
$\begin{eqnarray*} P(\Omega_M)& = & P(u_1|u_s=0) ... P(u_M|u_s=0) P(u_s=0) \\ ~ & + & P(u_1|u_s=1) ... P(u_M|u_s=1) P(u_s=1) \end{eqnarray*}$

Parámetros

[in]	OmegaM	$\Omega_M$ es un caso de ocurrencia del vector binario.
[in]	p	Probabilidades de error de los BSC, $P(u_m \neq u_s \| u_s) \equiv p_m,~\forall~m\in\{1,...,M\}$
[in]	us	Valor de a analizar.
[in]	ps	Probabilida de la fuente .
[out]	PjU0OmegaM	Retorna la probabilidad conjuta $P(u_s \Omega_M)$ .
[in]	Umbral	Umbral para binarizar $\Omega_M$ . $\Omega_M\leftarrow \Omega_M\geq Umbral$ .

Devuelve: Retorna la probabilidad condicionada $P(u_s |\Omega_M)$ .

◆ HjOmegaM()

double Pds::Ceo::Binary::Entropy::HjOmegaM	(	const Pds::Vector &	p,
		double	ps = `0.5`
	)

Encuentra la entropia conjunta $H(\Omega_M)\equiv H(u_1,...,u_M)$ para fontes generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s| u_s)=p_m$ [7] .

$H(\Omega_M)= -\sum_{u_1, u_2, ... u_M} P(\Omega_M)~log_2\left(P(\Omega_M)\right)$

Parámetros

[in]	p	Probabilidades de error de los BSC, $P(u_m \neq u_s \| u_s) \equiv p_m,~\forall~m\in\{1,...,M\}$
[in]	ps	Probabilida de la fuente .

Devuelve: Retorna la entropia conjuta $H(\Omega_M)\equiv H(u_1,...,u_M)$ para fuentes.

Ejemplos: example_ceo_model_entropy_joint.cpp.

◆ HjsOmegaM()

double Pds::Ceo::Binary::Entropy::HjsOmegaM	(	double	rho,
		unsigned int	M,
		double	ps = `0.5`
	)

Encuentra la entropia conjunta $H(\Omega_M) \equiv h_{J}(\rho,M)$ para fontes generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s| u_s)=p_m\equiv \rho$ [1].

$h_{J}(\rho,M,p_s)= -\sum_{k=0}^{M} {M \choose k} P_k(\rho,M,p_s)~log_2 ( P_k(\rho,M,p_s) )$

donde:

$P_k(\rho,M,p_s)= (1-p_s)\rho^k (1-\rho)^{M-k} + p_s~ \rho^{M-k} (1-\rho)^{k} \}$

Parámetros

[in]	rho	Es la probabilidad de error de los canales BSC. $P(u_m \neq u_s\| u_s)=\rho$ .
[in]	M	Es el número de canales BSC.
[in]	ps	Probabilida de la fuente .

Devuelve: La entropia conjunta $H(\Omega_M)\equiv h_{J}(\rho,M,p_s)$ .

Ejemplos: example_ceo_model_entropy_joint.cpp.

◆ HjsOmegaMInv()

double Pds::Ceo::Binary::Entropy::HjsOmegaMInv	(	double	HJoint,
		short int	M,
		double	ps = `0.5`
	)

Encuentra el valor $\rho$ que genera la entropia conjunta $H(\Omega_M) \equiv h_{J}(\rho,M)$ para fontes generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s| u_s)=p_m\equiv \rho$ [1] [2].

$h_{J}(\rho,M,p_s)= -\sum_{k=0}^{M} {M \choose k} P_k(\rho,M,p_s)~log_2 ( P_k(\rho,M,p_s) )$

donde:

$P_k(\rho,M,p_s)= (1-p_s)\rho^k (1-\rho)^{M-k} + p_s~ \rho^{M-k} (1-\rho)^{k} \}$

.

Comentarios: Esta funcion es la inversa de Pds::Ceo::Binary::Entropy::HjsOmegaM(). Cuando HJoint y son entregados la funcion retorna el valor de $\rho$ .

Parámetros

[in]	HJoint	Entropia conjunta $H(\Omega_M) \equiv h_{J}(\rho,M)$ .
[in]	M	Es el número de canales BSC.
[in]	ps	Probabilida de la fuente .

Devuelve: Retorna $\rho=P(u_m \neq u_s| u_s)$ que es la probabilidad de error de los canales BSC. La busqueeda finaliza quando $|HJoint-h_{J}(\rho,M)|<|E(HJoint)/1000000|$ , .

Ejemplos: example_ceo_model_entropy_joint.cpp.

◆ HcUsOmegaM()

double Pds::Ceo::Binary::Entropy::HcUsOmegaM	(	const Pds::Vector &	p,
		double	ps
	)

Encuentra la entropia condicionada. $H(u_s|\Omega_M)$ [5].

Dadas fontes generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s| u_s)\equiv p_m$ [5] .

$H(u_s|\Omega_M)= -\sum_{u_s,u_1, u_2, ... u_M} P(u_s,\Omega_M)~log_2(P(u_s|\Omega_M))$

Parámetros

[in]	p	Probabilidades de error de los BSC, $P(u_m \neq u_s \| u_s) \equiv p_m,~\forall~m\in\{1,...,M\}$ .
[in]	ps	Probabilida de la fuente .

Devuelve: HCond Entropia condicionada. $H(u_s|\Omega_M)$ .

Ejemplos: example_ceo_model_entropy_cond.cpp y example_ceo_model_fusion2.cpp.

◆ HcsUsOmegaM() [1/2]

double Pds::Ceo::Binary::Entropy::HcsUsOmegaM	(	double	rho,
		unsigned int	M,
		double	ps = `0.5`
	)

Encuentra la entropia condicionada $H(u_s|\Omega_M)\equiv h_{C}(\rho,M,p_s)$ [5] pp.37.

Dadas fontes generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s| u_s)\equiv p_m\equiv \rho$ [5] pp.37.

Si

$h_{C}(\rho,M,0.5)= \sum_{k=0}^{M} {M \choose k} \rho^k (1-\rho)^{M-k}~log_2 \left ( 1 + \{ \frac{\rho}{1-\rho} \}^{M-2 k} \right )$

Si $p_s\neq 0.5$

$h_{C}(\rho,M,p_s)= h_b(p_s)+M~h_b(\rho)-h_{J}(\rho,M,p_s)$

Donde y $h_{J}(\rho,M,p_s)$ es la función Pds::Ceo::Binary::Entropy::HjsOmegaM().

Parámetros

[in]	rho	Es la probabilidad de error de los canales BSC. $P(u_m \neq u_s\| u_s)=\rho$ .
[in]	M	Es el número de canales BSC.
[in]	ps	Probabilida de la fuente .

Devuelve: Retorna la entropia condicionada $H(u_s|\Omega_M)\equiv h_{C}(\rho,M,p_s)$ .

Ejemplos: example_ceo_model_entropy_cond.cpp.

◆ HcsUsOmegaM() [2/2]

Pds::Vector Pds::Ceo::Binary::Entropy::HcsUsOmegaM	(	const Pds::Vector &	Rho,
		unsigned int	M,
		double	ps = `0.5`
	)

Encuentra la entropia condicionada $H(u_s|\Omega_M)\equiv h_{C}(\rho,M,p_s)$ [5] pp.37.

Dadas fontes generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s| u_s)\equiv p_m\equiv \rho$ [5] pp.37.

Si

$h_{C}(\rho,M,0.5)= \sum_{k=0}^{M} {M \choose k} \rho^k (1-\rho)^{M-k}~log_2 \left ( 1 + \{ \frac{\rho}{1-\rho} \}^{M-2 k} \right )$

Si $p_s\neq 0.5$

$h_{C}(\rho,M,p_s)= h_b(p_s)+M~h_b(\rho)-h_{J}(\rho,M,p_s)$

Donde y $h_{J}(\rho,M,p_s)$ es la función Pds::Ceo::Binary::Entropy::HjsOmegaM().

Parámetros

[in]	Rho	Es un vector de probabilidades de error para los canales BSC. $P(u_m \neq u_s\| u_s)=\rho$ .
[in]	M	Es el número de canales BSC.
[in]	ps	Probabilida de la fuente .

Devuelve: Retorna la entropia condicionada $H(u_s|\Omega_M)\equiv h_{C}(\rho,M,p_s)$ para cada valor de Rho[m].

◆ HcsUsOmegaMInv()

double Pds::Ceo::Binary::Entropy::HcsUsOmegaMInv	(	double	HCond,
		short int	M,
		double	ps = `0.5`
	)

Encuentra la inversa $\rho$ de la entropia condicionada $H(u_s|\Omega_M)\equiv h_{C}(\rho,M,p_s)$ para fontes generadas pasando una fuente , con probabilidade , atraves de canales BSC con probabilidades de error $P(u_m \neq u_s| u_s)=p_m\equiv \rho$ [5] pp.37, [4].

Si

$h_{C}(\rho,M,0.5)= \sum_{k=0}^{M} {M \choose k} \rho^k (1-\rho)^{M-k}~log_2 \left ( 1 + \{ \frac{\rho}{1-\rho} \}^{M-2 k} \right )$

Si $p_s\neq 0.5$

$h_{C}(\rho,M,p_s)= h_b(p_s)+M~h_b(\rho)-h_{J}(\rho,M,p_s)$

Donde y $h_{J}(\rho,M,p_s)$ es la función Pds::Ceo::Binary::Entropy::HjsOmegaM().

Comentarios: Esta funcion es la inversa de Pds::Ceo::Binary::Entropy::HcsUsOmegaM(). Cuando HJoint y son entregados la funcion retorna el valor de $\rho$ .

Parámetros

[in]	HCond	Entropia condicionada. $HCond=h_{C}(\rho,M,p_s)=H(u_s\|\Omega_M)$ .
[in]	M	Es el número de canales BSC.
[in]	ps	Probabilida de la fuente .

Devuelve: Retorna $\rho=P(u_m \neq u_s| u_s)$ que es la probabilidad de error de los canales BSC. La busqueeda finaliza quando $|HJoint-h_{J}(\rho,M,p_s)|<|E(HJoint)/1000000|$ , .